学习视频来源:麻省理工公开课_线性代数导论 讲师:Gilbert Strang
http://open.163.com/special/opencourse/daishu.html
Lecture 5 置换-转置-向量空间
Permutation and Transpose 置换和转置
接着上节课的内容,我们来更详细地了解下置换和转置。
Permutation 置换
置换矩阵记作 ,是行重新排列了的单位矩阵,用来完成行互换。当求解 存在主元为 0 的情况时,方程式变为 。对任意可逆矩阵 ,都有这种形式。
所有 置换矩阵的个数为 (n factorial n的阶乘),且所有的置换矩阵可逆 。
Transpose 转置
已知一个 的矩阵 ,则 。用符号表示为 。
若 ,则 为symmetric matrix 对称矩阵(方阵)。
那么怎样通过rectangular matrix 长方阵 得到对称矩阵呢?我们只需要将 和其转置 相乘。先看上面的特例:
再用符号进行推算:
Vector Space 向量空间 The beginning of real Linear Algebra
满足一定规则的空间才可以被称为向量空间,必须能进行 add 加法和 multiply 数乘运算,必须能进行线性组合。
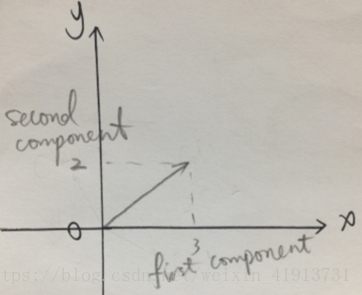
二维real vectors 实向量的向量空间
里可能有 , (零向量是所有向量里最重要的), 。我们可以将它们相加,点乘,其计算结果仍在 里。画图,横坐标表示第一个分量,纵坐标表示第二个分量。
我们可以把 称为一个平面,如果拿掉其中的一个向量比如零向量,就像是在平面上戳了一个洞,这会非常糟糕。对于向量空间,必须满足存在于此空间的向量乘以任何数后都在向量空间。乘以 0 也是如此,因此所有的向量空间都必须包含零向量。怎样找出 的子空间?
对于 内一条穿过原点(数乘允许乘以 0)的直线上的任意向量,乘以任意数的结果均在这条直线上,即对数乘封闭。而直线上的任意向量,加上直线上的任意向量,结果仍在直线上,即对加法封闭。所以 内的一条直线是 的一个子空间。
列出 的所有子空间:① 本身(最大的子空间);②穿过原点,两边无限延伸的直线;③零向量 (最小的子空间)。
已知矩阵 ,如何构造子空间?
通过列向量构造子空间。
中的各列均为 中的向量,这两列所有的线性组合(包括数乘和加法)构成一个子空间,即column space 列空间,记 。