Lecture 5:Kernel Logistic Regression
Soft-Margin SVM as Regularized Model
我们首先回顾Soft-Margin SVM的优化目标
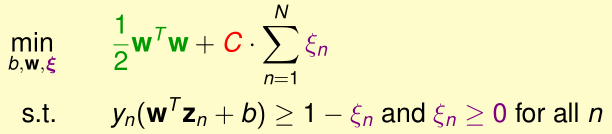
在得到的最优解\((b,w,\xi)\)中,当\((x_n,y_n)\)没有越过margin自己这一方的边缘,则\(\xi_n=0\),否则\(\xi_n=1-y_n(w^Tz_n+b)\)
所以\(\xi_n=\max(1-y_n(w^Tz_n+b),0)\)
于是我们可以写出Soft-Margin SVM优化目标无约束的形式:
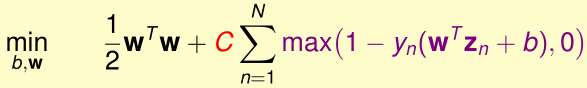
如果我们令单点误差\(err_n=\max(1-y_n(w^Tz_n+b),0)\),\(C=\frac 1 \lambda\),上面的优化目标等价于
\[\min \frac \lambda 2 w^Tw+\sum_{n=1}^N err_n\]
这很类似单点误差为\(err_n\),加入了L2正则化的误差函数
为什么Soft-Margin SVM不直接优化这个问题呢?因为它不是二次规划问题,也不能使用核技巧,并且max(...)也是不可导的
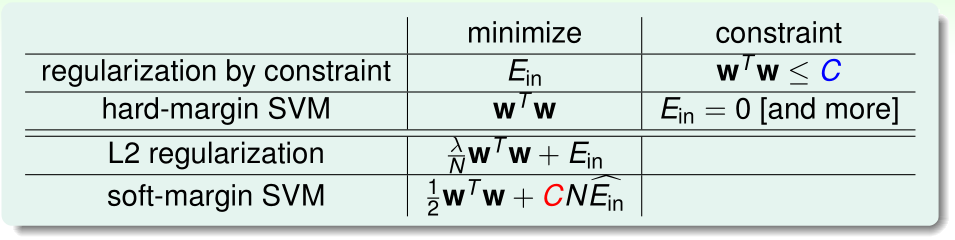

我们比较L2正则化的\(\lambda\)与Soft-Margin SVM的惩罚系数C:
- L2正则化中,\(\lambda\)越小,正则化程度越小
- Soft-Margin SVM中,C越大,正则化程度越小
SVM versus Logistic Regression
令\(s=w^Tz_n+b\),我们比较Soft-Margin SVM、PLA(以及口袋算法)、逻辑回归的单点误差函数:
- Soft-Margin SVM:\(err_{SVM}=\max(1-ys,0)\)
- PLA/Pocket:\(err_{0/1}=1\{ys\leq 0\}\)
- 逻辑回归:\(err_{CE}=\ln(1+\exp(-ys))=(\ln 2) err_{SCE}\)
- Scaled Cross Entropy:\(err_{SCE}=\log_2(1+\exp(-ys))\)
\(err_{SVM},err_{0/1},err_{SCE}\)图像如下图所示:

可见\(err_{SCE}\geq err_{0/1}\),\(err_{SVM}\geq err_{0/1}\),SVM和逻辑回归都是通过最优化凸函数\(err_{SVM}(err_{CE})\)来给\(err_{0/1}\)确定一个很小的上界,从而保证可以实现二分类
SVM的单点误差\(err_{SVM}\)又称为Hinge损失
因为\(ys\to +\infty\)时\(err_{SVM}\to 0,err_{CE}\to 0\);\(ys\to -\infty\)时\(err_{SVM}\to -ys,err_{CE}\to -ys\),所以Soft-Margin SVM类似于加L2正则化的逻辑回归
SVM for Soft Binary Classification
我们能否用Soft-Margin SVM求出的参数\(w,b\),类似逻辑回归那样,预测某个未知样本属于正/负样本的概率呢?下面介绍输出分类概率的SVM:Probabilistic SVM(该方法最早由Platt提出,叫Platt scaling)
- 1、首先在训练集\(\mathcal D\)上用Soft-Margin SVM训练出参数\((b_{SVM},w_{SVM})\),并令\(z_n'=w_{SVM}^T\Phi(x_n)+b_{SVM}\)
- 2、用N个\((z_n',y_n)\)作训练集,训练一个逻辑回归模型:\(g(x)=\theta(Az_n'+B)\),一般如果\((b_{SVM},w_{SVM})\)比较合适的话,\(A>0,B\approx 0\)
- 3、最终得到的Probabilistic SVM的假设函数就是\(g(x)=\theta(A(w_{SVM}^T\Phi(x_n)+b_{SVM})+B)\),g(x)就是输入特征为x时分类为正样本1的概率
Kernel Logistic Regression
这种方法可以看作是用Soft-Margin Kernel SVM在\(\mathcal Z\)空间内对逻辑回归的一种近似,那么能否直接精确求出\(\mathcal Z\)空间内逻辑回归的解呢?
首先介绍表示定理(Representer Theorem):对于所有带L2正则化的线性模型,
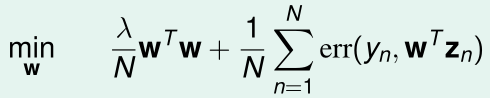
其最优解\(w^*=\sum_{n=1}^N\beta_nz_n\),即w的最优解可以表示成所有输入特征的线性组合
证明:
首先把最优解拆成两个相互正交的分量:\(w^*=w_{||}+w_{\perp}\)
其中\(w_{||}\in \mathrm{span}(z_1,\cdots,z_N)\)(\(z_n\)的生成子空间),\(w_{\perp}\perp \mathrm{span}(z_1,\cdots,z_N)\)
假设\(w_{\perp}\neq 0\),现在我们比较\(w^*,w_{||}\)的损失函数值:
(1)二者的单点误差\(err\)相同:\(err(y_n,w^{*T}z_n)=err(y_n,(w_{||}+w_{\perp})^Tz_n)=err(y_n,w_{||}^{T}z_n+0)\)
(2)\[w^{*T}w^*=(w_{||}+w_{\perp})^T(w_{||}+w_{\perp})\]\[=w_{||}^Tw_{||}+2w_{||}^Tw_{\perp}+w_{\perp}^Tw_{\perp}\]
\[=w_{||}^Tw_{||}+w_{\perp}^Tw_{\perp}> w_{||}^Tw_{||}\]
可见,\(w^*\)的损失函数值比\(w_{||}\)大,最优解应该是\(w_{||}\),与假设矛盾,所以\(w^*=w_{||}\in\mathrm{span}(z_1,\cdots,z_N)\)
而在预测输入z的输出值时,我们需要将\(w^*\)与\(z\)做内积,表示定理保证了,此时可以用N个\(z_n\)与当前输入\(z\)的内积替代\(w^*\)与\(z\)的内积,进一步地,可以用核函数代替这N个内积
这表明,所有带L2正则化的线性模型都可以使用核技巧
回顾带L2正则化的逻辑回归的优化目标:
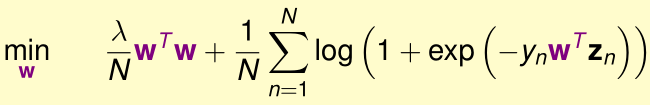
将\(w=\sum_{n=1}^N\beta_nz_n\)代入,并用核函数代替内积,优化目标变成了:
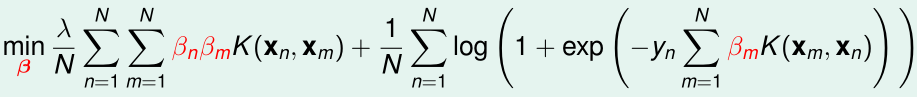
要最优化的参数变成了N个:\(\beta_1,\cdots,\beta_N\)
这就是Kernel Logistic Regression(KLR),这个优化目标使用批量/随机梯度下降等方法,最优化参数即可
若令\(\beta=(\beta_1,\cdots,\beta_N)^T\),N阶矩阵K,\(K_{ij}=K(x_i,x_j)\),则优化目标中的正则化项\(\sum_{n=1}^N\sum_{m=1}^N\beta_n\beta_mK(x_n,x_m)=\beta^TK\beta\)
需要注意的是,这里的\(\beta_n\)与SVM的拉格朗日乘子\(\alpha_n\)不同,\(\alpha_n\)一般来说大部分为0,而\(\beta_n\)大部分是非零的。