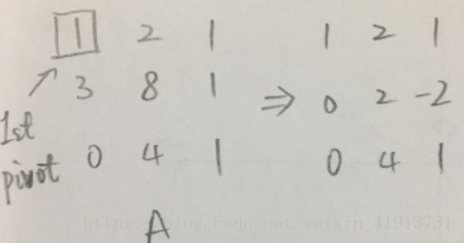麻省理工大学线性代数导论笔记 - Lecture 2 矩阵消元

学习视频来源：麻省理工公开课_线性代数导论 讲师：Gilbert Strang

http://open.163.com/special/opencourse/daishu.html

---

Lecture 2 矩阵消元

Elimination 消元法

$\begin{cases} x+2y+z=2&①\\ 3x+8y+z=12&②\\ 4y+z=2&③ \end{cases}$ <=> $Ax=b$

$\left( \begin{array}{ccc} 1 & 2 & 1\\ 3 & 8 & 1\\ 0 & 4 & 1 \end{array} \right)$ <=> $A$

• Elimination works 消元法奏效

  只要$A$是一个不可逆/非奇异矩阵，消元法就会奏效。消元法的核心概念是 matrix operations 矩阵变换。

  • 第一步：假设方程①成立，消去方程②和③的$x$。

  首先，用方程①乘以一个elimination multiplier 消元乘数，然后从方程②中将其减去。这里用框框圈起来的 1 是消元的关键，被称为1st pivot 主元 1。因为第一行是主元行，所以不变。消元乘数取 3。

  这里方程③的$x$的系数已经是 0。理论上是用方程①乘以消元乘数 0，然后从方程③中将其减去，但我们可以直接跳到下一步。
  

  • 第二步：进行递归，接着消去方程③的$y$

  方法同上，用方程②乘以消元乘数，然后从方程③中将其减去。现在第二行用框框圈起来的 2 被称为2nd pivot 主元 2，第二行是主元行。消元乘数取 2。得到矩阵$U$，$U$表示upper triangular 上三角矩阵。
  

  • 注：先算完左侧矩阵$A$的消元，之后再加上右侧向量$b$；主元不能为 0；determinant 行列式等于主元之积。

• Elimination fails 消元法失效

  失效，指的是不能得到三个主元。如果 0 占据了主元的位置，这时就要进行switch rows 行交换，在下面的方程中找出合适的主元。当底下的行中再也没有非 0 元素时，这时消元确定失效。

  扫描二维码关注公众号，回复： 2505360 查看本文章

Back-substitution 回代

这时我们引入右侧向量$b$作为$A$的新一列，称为augmented matrix 增广矩阵。

$\left( \begin{array}{ccc} 1 & 2 & 1 & 2\\ 3 & 8 & 1 & 12\\ 0 & 4 & 1 & 2 \end{array} \right)$ <=> $\left( \begin{array}{ccc} A & b \end{array} \right)$

$c$是$b$的最终结果，就像$U$是$A$的最终结果。

以下就是矩阵$U$和$b$的方程含义，我们可以轻松解出$x$、$y$、$z$的值。

$\begin{cases} x+2y+z=2\\ 2y-2z=6\\ 5z=-10 \end{cases}$ <=> $Ux=c$

---

附一：进行矩阵乘法时，注意用整个向量来思考：

• row operations 行变换——矩阵行的线性组合

  $\left( \begin{array}{ccc} 1 & 2 & 3\end{array} \right)$$\left( \begin{array}{ccc} row1\\ row2\\row3\end{array} \right)=1×row1+2×row2+3×row3$

• column operations 列变换——矩阵列的线性组合

  $\left( \begin{array}{ccc} col1 & col2 & col3\end{array} \right)$$\left( \begin{array}{ccc} 1\\ 2\\3\end{array} \right)=1×col1+2×col2+3×col3$

---

Elimination matrices 消元矩阵

• 第一步：找到一个elementary matrix 初等矩阵$E_{2,1}$（因为它表示位置2,1上的变换），从$A$中的行二减去 3 倍行一，其他行不变。

  $\left( \begin{array}{ccc} 1 & 0 & 0\\ -3 & 1 & 0\\ 0 & 0 & 1 \end{array} \right)$ $\left( \begin{array}{ccc} 1 & 2 & 1\\ 3 & 8 & 1\\ 0 & 4 & 1 \end{array} \right)=\left( \begin{array}{ccc} 1 & 2 & 1\\ 0 & 2 & -2\\ 0 & 4 & 1 \end{array} \right)$ <=> $E_{2,1}A=\left( \begin{array}{ccc} 1 & 2 & 1\\ 0 & 2 & -2\\ 0 & 4 & 1 \end{array} \right)$

• 第二步：找到一个初等矩阵$E_{3,2}$（因为它表示位置3,2上的变换），从中$E_{2,1}A$的行三减去 2 倍行二，其他行不变。

  $\left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & -2 & 1 \end{array} \right)$$\left( \begin{array}{ccc} 1 & 2 & 1\\ 0 & 2 & -2\\ 0 & 4 & 1 \end{array} \right)= \left( \begin{array}{ccc} 1 & 2 & 1\\ 0 & 2 & -2\\ 0 & 0 & 5 \end{array} \right)$ <=>$E_{3,2}(E_{2,1}A)=U$

每一步用到一个初等矩阵，使$A$最终转换成$U$。那么是否存在一个矩阵，可以一次性完成从$A$到$U$的消元步骤？答案是Yes。根据矩阵的associative law 结合律，增减括号对任意矩阵乘法皆适用。即我们可以将$E_{3,2}(E_{2,1}A)=U$ 改为$(E_{3,2}E_{2,1})A=U$ ，则$E_{3,2}E_{2,1}= \left( \begin{array}{ccc} 1 & 0 & 0\\ -3 & 1 & 0\\ 6 & -2 & 1 \end{array} \right)$为我们所求的矩阵。

---

附二：permutation matrix 置换矩阵，交换矩阵行列的一类初等矩阵。

• 交换行

$\left( \begin{array}{ccc} 0 & 1\\ 1 & 0 \end{array} \right)$$\left( \begin{array}{ccc} a & b\\ c & d\end{array} \right)=\left( \begin{array}{ccc} c & d\\ a & b\end{array} \right)$

• 交换列

$\left( \begin{array}{ccc} a & b\\ c & d \end{array} \right)$$\left( \begin{array}{ccc} 0 & 1\\ 1 & 0\end{array} \right)=\left( \begin{array}{ccc} b & a\\ d & c\end{array} \right)$

---

Inverses 逆变换

我们现在希望能将$U$转换为$A$。那么就要找到一个矩阵能取消这次消元，即该矩阵乘以$E_{3,2}$、$E_{2,1}$会得到identity matrix 单位矩阵。以消元矩阵的第一步为例，要使$E_{2,1}$转换为单位矩阵，则需用行二加上 3 倍的行一：

$\left( \begin{array}{ccc} 1 & 0 & 0\\ 3 & 1 & 0\\ 0 & 0 & 1 \end{array} \right)$ $\left( \begin{array}{ccc} 1 & 0 & 0\\ -3 & 1 & 0\\ 0 & 0 & 1 \end{array} \right)=\left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right)$ <=> $E^{-1}_{2,1}E_{2,1}=I$