一、向量(Vectors)
向量表示示意图:

- 有序实数组,用以表示在不同坐标轴上的投影长度
- 有行和列两种表达方式,在图形学中常以列表达
- 代表了一个有方向的长度
- 基本运算:
- 加法(满足结合律和交换律)
- 标量乘以向量(满足结合律和分配率)
- 点乘(内积,结果为标量,几何意义是 [公式] ,满足分配率和交换律,可用于判断两向量夹角,求向量长度,计算投影等)
- 叉乘(外积,结果为向量,垂直于原向量构建的平面,长度为 [公式] ,交换叉乘中两向量的位置,会得到长度相同但方向相反的向量)
- 向量归一化:p的归一化向量q与p方向相同,长度为1,可通过点乘算出
(一)向量归一化
向量长度表示:\(||\vec a||\)
单位向量:
- 长度 = 1
- 计算公式:
\[ \hat a = \frac{\vec a}{||\vec a||} \] - 可用于代表方向
(二)向量相加
向量相加示意图:
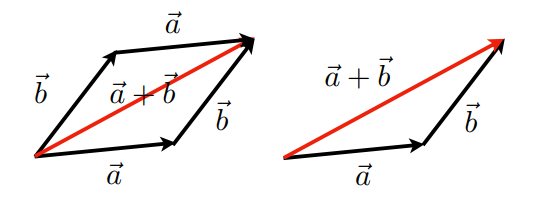
- 几何:遵守平行法则、三角法则
- 代数上:坐标相加
(三)笛卡尔积
向量相加示意图:
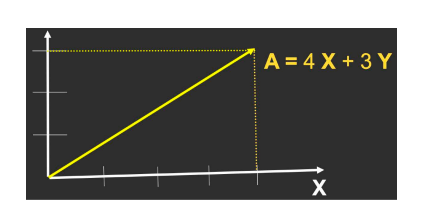
X和Y可以是任何(通常是正交的单位)向量,
\(A = {x \choose y }\) \(A^T = \left(x,y \right )\) \(||A|| = \sqrt{x_2+y_2}\)
(四)向量相乘
1. 点乘
向量点乘示意图:
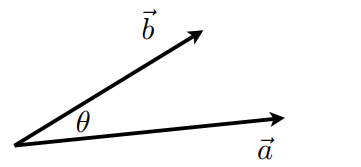
\(\vec a \cdot \vec b = \left\| \vec a \right\| \left\| \vec b \right\| \cos \theta\) \(\cos \theta = \frac{\vec a \cdot \vec b}{\left\| \vec a \right\| \left\| \vec b \right\|}\)
对于单位向量: \(\cos \theta = \hat a \cdot \hat b\)
(1)点乘性质
\(\vec a \cdot \vec b = \vec b \cdot \vec a\)
\(\vec a \cdot \left( \vec b + \vec c \right) = \vec a \cdot \vec b + \vec a \cdot \vec c\)
\(\left( k \vec a \right) \cdot \vec b = \vec a \cdot \left( k \vec b \right) = k \left( \vec a \cdot \vec b \right)\)
(2)在笛卡尔坐标系中做点积
组合相乘,然后相加。
- 二维坐标系
\[ \vec a \cdot \vec b = {x_a \choose y_a} \cdot {x_b \choose y_b} = x_aX_b+y_ay_b \] - 三维坐标系
\[ \vec a \cdot \vec b = \begin{pmatrix} x_a \\ y_a \\ z_a \end{pmatrix} \cdot \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} = x_ax_b+y_ay_b+z_az_b \]
(3)投影点积
示意图:
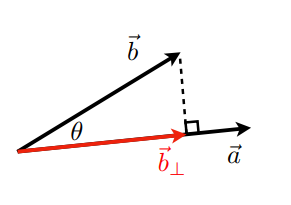
- \(\vec b_\bot\):\(\vec b\)在\(\vec a\)上的投影
- \(\vec b_\bot\)必须属于\(\vec a\)(或者属于\(\hat a\))
- \(\vec b_\bot = k \vec a\)
- 求k的值
- \(k = \left\| \vec b_\bot \right\| \cos \theta\)
- \(\vec b_\bot\)必须属于\(\vec a\)(或者属于\(\hat a\))
(4)图形学中的点乘
- 求两个向量的夹角,(例如:光源与表面夹角的余弦值)
- 求一个向量在另一个向量上的投影
应用
测量两个向量的方向
1)在一个圆中

例如,图中 \(\vec a \cdot \vec b >0\)属于前向(forward), \(\vec a \cdot \vec c <0\)属于后向(backward)
2)两个向量之间
