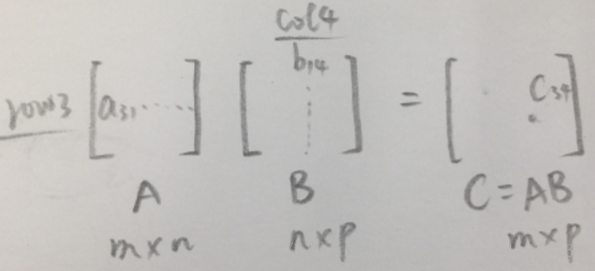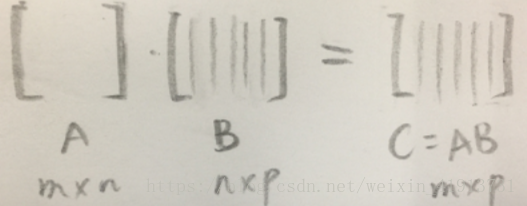麻省理工大学线性代数导论笔记 - Lecture 3 乘法与逆矩阵

学习视频来源：麻省理工公开课_线性代数导论 讲师：Gilbert Strang

http://open.163.com/special/opencourse/daishu.html

---

Lecture 3 乘法与逆矩阵

Matrix multiplication 矩阵乘法

• basic rules 一般性法则

  $C=A×B$。以$c_{3,4}$为例，$c_{3,4}$来自于$C$的行 3 列 4，其计算使用了点乘。$c_{3,4}=（row\ 3\ of\ A）·（column\ 4\ of\ B）=a_{3,1}×b_{1,4}+a_{3,2}×b_{2,4}+ ··· =\sum^n_{i=1}a_{3,i}×b_{i,4}$ 。
  
  矩阵相乘并不一定要求$A$和$B$都是square 方阵，但$B$的总行数，必须与$A$的总列数相等。

• matrix times columns 矩阵乘以列向量

  $B$可以考虑成p个单独的列向量。矩阵$A$乘以$B$的第一列，可以得到$C$的第一列。用$A$乘以$B$的每个列向量，相应的得到$C$的p个列向量。用线性组合的语言描述，即：$C$中的各列，是$A$中各列的线性组合。根据前文，$A$右乘以列向量，等价于$A$中的列进行线性组合。而$B$中的数字告诉我们，是怎样的线性组合。
  

• rows times matrix 行向量乘以矩阵

  $A$可以考虑成m个单独的行向量。矩阵$A$的第一行乘以$B$，可以得到$C$的第一行。用$A$的每个行向量乘以$B$，相应的得到$C$的m个行向量。用线性组合的语言描述，即：$C$中的各行，是$B$中各行的线性组合。根据前文，行向量左乘以$B$，等价于$B$中的行进行线性组合。而$A$中的数字告诉我们，是怎样的线性组合。
  

• columns times rows 列乘以行

  之前用一个行向量乘以一个列向量，我们可以得到一个数。假设$A$为$\left( \begin{array}{ccc} 2&7\\ 3&8\\ 4&9 \end{array} \right)$，$B$为$\left( \begin{array}{ccc} 1&6\\ 0&0 \end{array} \right)$，如果用$A$中的第一列乘以$B$中的第一行呢？我们将会得到一个矩阵：

  $\left( \begin{array}{ccc} 2\\ 3\\ 4 \end{array} \right)$$\left( \begin{array}{ccc} 1 & 6\end{array} \right)$=$\left( \begin{array}{ccc} 2&12\\ 3&18\\ 4&24 \end{array} \right)$

  能看到等号的右侧矩阵中，每一行都是$\left( \begin{array}{ccc} 1 & 6\end{array} \right)$的倍数，所有行都依赖于$\left( \begin{array}{ccc} 1 & 6\end{array} \right)$。如果画出这些行的向量，它们都是同一方向。这就是row space 行空间，即行的所有可能的线性组合。该矩阵的行空间是向量$\left( \begin{array}{ccc} 1 & 6\end{array} \right)$上的一条直线。

  同理，每一列都是$\left( \begin{array}{ccc} 2\\ 3\\ 4 \end{array} \right)$的倍数。画出列向量，也会是一个方向，其列空间也是一条直线。

  延续这个方法从第一列（行）到最后一列（行），可以得出一个结论：$AB$等于$A$各列与$B$各行乘积之和。

  $\left( \begin{array}{ccc} 2&7\\ 3&8\\ 4&9 \end{array} \right)$$\left( \begin{array}{ccc} 1&6\\ 0&0 \end{array} \right)$=$\left( \begin{array}{ccc} 2\\ 3\\ 4 \end{array} \right)$$\left( \begin{array}{ccc} 1 & 6\end{array} \right)$+$\left( \begin{array}{ccc} 7\\ 8\\ 9 \end{array} \right)$$\left( \begin{array}{ccc} 0 & 0 \end{array} \right)$

• block multiplication 分块乘法

  假设$A$和$B$都为方阵，同等大小（其实只要互相匹配，并不一定要大小相等）。分成大小匹配的四块，计算时相当于分块行乘以分块列。

  $\left( \begin{array}{ccc} A_1&A_2\\ A_3&A_4 \end{array} \right)$$\left( \begin{array}{ccc} B_1&B_2\\ B_3&B_4 \end{array} \right)$=$\left( \begin{array}{ccc} A_1B_1+A_2B_3&A_1B_2+A_2B_4\\ A_3B_1+A_4B_3&A_3B_2+A_4B_4 \end{array} \right)$

Inverse 逆（方阵）

前篇简单提到了逆变换，本段会详细地介绍矩阵的逆。

• 逆是否存在

  矩阵的逆是一个很重要的话题。方阵$A$是否可逆？如果逆矩阵存在，如何求逆？从前文我们得知，一个矩阵的逆和其本身相乘，结果为单位矩阵：$A^{-1}A=I$。注意这里的$A^{-1}$是left inverse 左逆，$A$的右边也可以存在某个逆矩阵：$AA^{-1}=I$。方阵的左逆等于右逆，如果是非方阵，则不相等（在广义逆矩阵的定义里，不仅方阵才有逆）。

  再看不可逆的情况。若$A$为$\left( \begin{array}{ccc} 1&3\\ 2&6 \end{array} \right)$，假设存在向量$X$使$AX=\vec{0}$，我们能得出$X$是非零向量$\left( \begin{array}{ccc} 3\\ -1 \end{array} \right)$$\left( \begin{array}{ccc} 1&3\\ 2&6 \end{array} \right)$$\left( \begin{array}{ccc} 3\\ -1 \end{array} \right)$=$\left( \begin{array}{ccc} 0\\ 0 \end{array} \right)$

  $X$不是$\vec{0}$向量非常重要。如果$AX=\vec{0}$，假设乘以$A$的逆，$A^{-1}AX=IX=X=\vec{0}$，和$X≠\vec{0}$矛盾，因此$A$不可逆。至此得到结论：不可逆（奇异）矩阵能通过非零向量$X$得到$\vec{0}$。

• Gauss-Jordan法求逆

  现有矩阵$A$=$\left( \begin{array}{ccc} 1&3\\ 2&7 \end{array} \right)$求逆，假设逆为$\left( \begin{array}{ccc} a&c\\ b&d \end{array} \right)$，则第一列满足$A$乘以它得到$\left( \begin{array}{ccc} 1\\ 0 \end{array} \right)$：$\left( \begin{array}{ccc} 1&3\\ 2&7 \end{array} \right)$$\left( \begin{array}{ccc} a\\ b \end{array} \right)$=$\left( \begin{array}{ccc} 1\\ 0 \end{array} \right)$，第二列满足$A$乘以它得到$\left( \begin{array}{ccc} 0\\ 1 \end{array} \right)$：$\left( \begin{array}{ccc} 1&3\\ 2&7 \end{array} \right)$$\left( \begin{array}{ccc} c\\ d \end{array} \right)$=$\left( \begin{array}{ccc} 0\\ 1 \end{array} \right)$。我们发现求逆其实和解两个方程组是一回事，不同的是这里有两个右侧向量$b$。

  现在引出Gauss-Jordan思想，在本例中，即同时解出以上两个方程组。还记得增广矩阵的情况吗，也就是同时照顾到右侧向量的情况。我们将采取消元法（Gauss的方法），使左侧变为单位阵：

  第一步，第二行减去 2 倍的第一行，得到上三角矩阵。Gauss做到这就不管了，但Jordan还会继续；第二步，第一行减去 3 倍的第二行以消去左侧矩阵第一行第二列的“3”。这时右侧的矩阵即为$A^{-1}$。

  $\left ( \begin{array}{c:c} \begin{matrix} 1&3\\ 2&7 \end{matrix}& \begin{matrix} 1&0\\ 0&1 \end{matrix} \end{array} \right )$—>$\left ( \begin{array}{c:c} \begin{matrix} 1&3\\ 0&1 \end{matrix}& \begin{matrix} 1&0\\ -2&1 \end{matrix} \end{array} \right )$—>$\left ( \begin{array}{c:c} \begin{matrix} 1&0\\ 0&1 \end{matrix}& \begin{matrix} 7&-3\\ -2&1 \end{matrix} \end{array} \right )$

  为了解释Gauss-Jordan法的原理，我们引入消元矩阵$E$，因为$A$经过消元步骤一步步得到了$I$

  $E\left ( \begin{array}{c:c} \begin{matrix} A \end{matrix}& \begin{matrix} I \end{matrix} \end{array} \right )$=$？\left ( \begin{array}{c:c} \begin{matrix} I \end{matrix}& \begin{matrix} ？\end{matrix} \end{array} \right )$

  上图可知$E$乘以$A$等于单位阵，即$E$必然是$A$的逆。而$E$乘以单位阵仍等于$E$，所以可以写成下图形式，这就是Gauss-Jordan消元。

  $E\left ( \begin{array}{c:c} \begin{matrix} A \end{matrix}& \begin{matrix} I \end{matrix} \end{array} \right )$=$\left ( \begin{array}{c:c} \begin{matrix} I \end{matrix}& \begin{matrix} A^{-1} \end{matrix} \end{array} \right )$