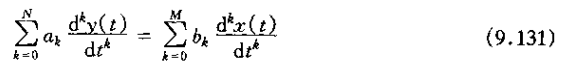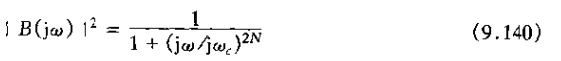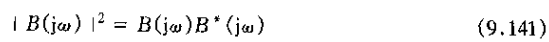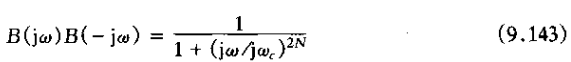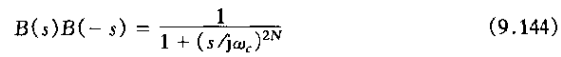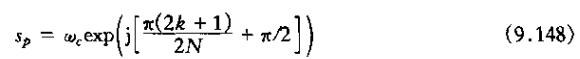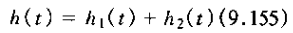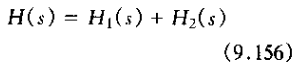注:本博客是基于奥本海姆《信号与系统》第二版编写,主要是为了自己学习的复习与加深。
一、用拉普拉斯变换分析与表征线性时不变系统
1、在拉普拉斯变换的范畴内,一般称H(s)为系统函数或转移函数。线性时不变系统的很多性质都与系统函数在s平面的特性密切有关。
一)、因果性、
1、一个因果系统的系统函数的收敛域时某半个右半平面。
2、对于一个具有有理系统函数的系统来说,系统的因果性就等效于最右边极点的右边的右半平面。
3、如果系统的单位冲激响应在t>0,h(t)=0,就说该系统是反因果的。同样,一般来说其相反的结论是不成立的;u,如果H(s)的收敛域是某左半平面,那么我们所知道的只是h(t)是左边的。然后,如果H(s)是有理的,那么收敛域位于最左边极点的左边就等效于系统是反因果的。
二)、稳定性
1、当且仅当系统函数H(s)的收敛域包括jw轴,即RE{s}=0时,一个线性时不变系统就是稳定的。
2、当且仅当H(s)的全部极点都位于s平面的左半平面时,叶即全部极点都有负实部时,一个具有有理系统函数H(s)的因果系统才是稳定的。
三)、由线性常系数微分方程表征的线性时不变系统
1、考虑如下形式的线性常系数微分方程:
在上式两边进行拉普拉斯变换,并反复应用线性和微分性质,可得
或
因此,一个由微分方程表征的系统,其系统函数总是有理的,它的零点就是如下方程的解;
而它的极点就是如下方程的解;
式(9.133)并没有包括H(s)收敛域的说明,因为该线性常系数微分方程本身没有限制收敛域。然而,如果给出系统有关稳定性和因果性的附加说明,收敛域就可以被推演出来。
三)、巴特沃思滤波器
1、一个N阶低通巴特沃思滤波器频率响应的模平方是
其中N是滤波器的阶。从式(9.140)要确定系统函数B(s),该系统函数可给出|B(jw)|2的特性。首先定义
如果将该巴特沃思滤波器的单位冲激响应限制为实值函数,那么由博里叶变换的共轭对称性质,就有
这样
注意到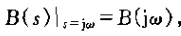
这个分母多箱子的根就是B(s)B(-s)的极点,这些极点应位于
式(9.145)对如下s=sp都满足
也即
关于B(s)B(-s)的极点,一般可以给出如下几个判断:
1)、在s平面内,半径为wc的圆上,有2N个极点在角度上呈等分割配置。
2)、极点永远不会位于jw轴上,而且当N为奇数时,在
3)、相邻极点之间的角度差是π/N弧度。
二、系统函数的代数属性与方框图表示
一)、线性时不变系统互联的系统函数
1、考虑两个系统的互联,如图9.30(a)所示。
总系统的单位冲激响应是
由拉普拉斯变换的线性性质,有
同理,两个系统的级联,如图9.30(b)所示,其单位冲激响应为
系统函数为
通过代数运算,在表示线性系统的互联时利用拉普拉斯变换,可以扩展到远比图9.30这种简单的并联和级联更为复杂的互联中去。
二)、由微分方程和有理系统函数描述的因果线性时不变系统的方框图表示
1、方框图类型可分为直接型,级联型,和并联型。
三、单边拉普拉斯变换
1、一个连续时间信号x(t)的单边拉普拉斯变换X(s)定义为
这里,积分下限时0-,以表明在积分区间内包括了几种t=0的任何冲激或高阶奇异函数。对于一个信号及其单边拉普拉斯变换,再次采用一个方便额简化符号为
比较式(9.170)和式(9.3)即可发现,单边和双边拉皮拉斯变换在定义上的不同在于积分的下限。
一)、单边拉普拉斯变换性质
二)、利用单边拉普拉斯变换求解微分方程
1、单边拉普拉斯变换的一个主要应用是求解具有非零初始条件的线性常系数微分方程。