傅立叶变换和拉普拉斯变换

欧拉公式

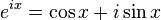
证明过程如下
首先是泰勒展开



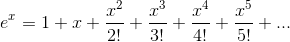
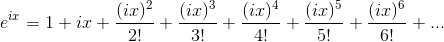
参考cosX和sinX的泰勒展开可以证明这个问题。
还有下面这个号称宇宙最美公式

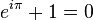
“自然底数e，自然数1和0，虚数i还有圆周率pi，它是这么简洁，这么美丽啊！”

傅立叶级数

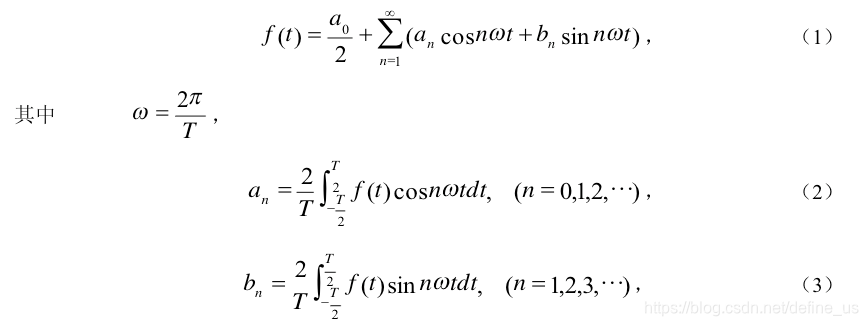
傅立叶在提出傅立叶变换时，坚持认为任何一个周期信号都可以展开成傅立叶级数。但是实际上不然，狄里赫利认为一个周期信号必须满足下面条件

1. 函数在任意有限区间内连续，或只有有限个第一类间断点（当t从左或右趋于这个间断点时，函数有有限的左极限和右极限）
2. 在一个周期内，函数有有限个极大值或极小值。
3. x(t)在单个周期内绝对可积，即
   

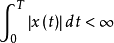
下面，我们尝试将上述式子转化为指数形式

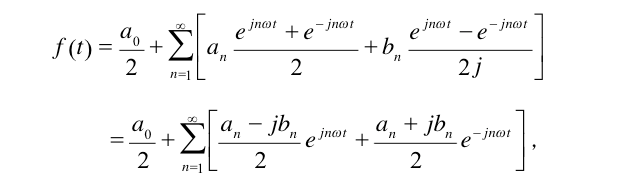
令

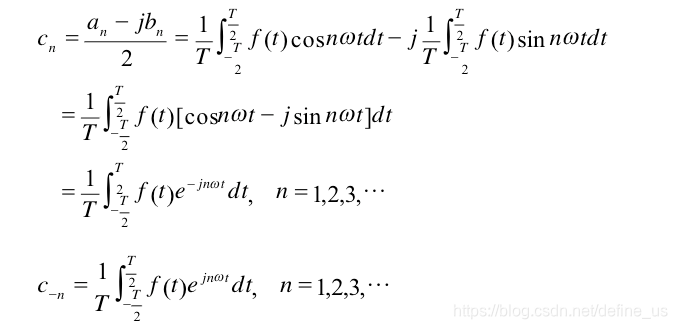
上面合并也就是

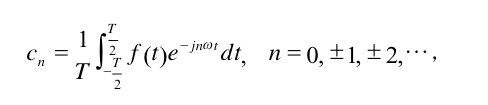
我们得到了

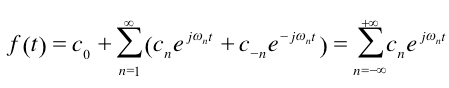
或者写成

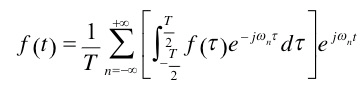
其中

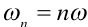
傅立叶变换

傅立叶变换必须针对一个周期函数，或者是针对一个只有一段定义域的函数（我们可以对其进行周期延拓）。但是，如果一个函数的周期是无限大呢？那么，她就是傅立叶变换。

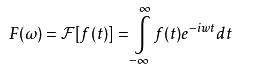
可以证明，如果是时域的信号是实信号，那么对应的傅立叶变换的是实部一定为偶函数。

进行频谱分析时，我们最关注的并非时实部和虚部。而是幅度和相位。
显然根据上面所说的狄里赫利条件，一个函数要能做傅立叶变换必须在正负无穷内绝对可积。当然，很多函数并不符合这个条件。

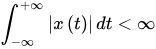
拉普拉斯变换

为了让一个并非时域绝对可积的函数进行傅立叶变换，我们将它乘以一个指数函数来进行衰减，只就是拉普拉斯变换。

离散傅立叶变换

小波变换