【信号与系统学习笔记】—— 拉普拉斯反变换+由零极点图对傅里叶变换几何求值

在开始本文的学习之前，大家需要记忆两种特殊形式的信号所对应的拉氏变换以及其对应的 ROC 区域：

1. 信号 $x(t) = e^{-at}u(t)$，其拉氏变换为： $X(s) = \frac{1}{s+ a}$，ROC为： $Re\{s\} > -a$（也就是以 $σ = -a$ 为轴右边的所有区域）
2. 信号 $x(t) = -e^{-at}u(-t)$，其拉氏变换为： $X(s) = \frac{1}{s+a}$，ROC为： $Re\{s\} < -a$（也就是以 $σ = -a$ 为轴左边的所有区域）
   通过上面的例子可以知道：不同信号的拉氏变换的表达式有可能一模一样，但是其 ROC 是不一样的。因此在表述一个信号的拉氏变换时，需要将表达式和 ROC 一起说明。这样才能完全确定一个信号。

一、拉普拉斯反变换

最实在的求拉普拉斯反变换的方法就是——将 $X(s)$ 做部分分式展开，原 $X(s)$ 就可以拆成几个有理分式的和或者是差。然后根据我们上面引言部分需要记忆的两种拉氏变换对，再结合 ROC 区域，确定出原信号的表达式。

---

听起来可能有点绕，我们直接看一个例子你就会了：

例：假设 $X(s) = \frac{1}{(s+1)(s+2)}, \quad -2<Re\{s\} < -1$
求它的拉普拉斯逆变换 $x(t)$

【第一步】：将 $X(s)$ 展开： $X(s) = \frac{1}{(s+1)(s+2)} = \frac{1}{s+1} - \frac{1}{s+2}$
【第二步】：分一个部分分式： $\frac{1}{s+1}$ 、 $\frac{1}{s+2}$ 都是引言中所提到的两种信号之一的拉氏变换。以 $\frac{1}{s+1}$ 为例：它可以是 $e^{-t}u(t)$，ROC为： $Re\{s\} > -1$；另外也有可能是 $-e^{-t}u(-t)$，ROC为： $Re\{s\} < -1$

【第三步】我们画出 $X(s)$ 的ROC：

我们可以看出是一个带状区域。

【第四步】：凑ROC。我们就看 $\frac{1}{s+1}$ 、 $\frac{1}{s+2}$的 ROC到底是哪种组合，他们的交集才是这样 [-2, -1] 的带状区域。我们发现：当 $\frac{1}{s+1}$ 的 ROC为： $Re\{s\} < -1$； $\frac{1}{s+2}$的 ROC为 ： $Re\{s\} > -2$ 的组合时，他们的交集才是这样的带状区域。

【第五步】：确定信号。已知了ROC，又知道了拉氏变换的表达式，就可以唯一确定信号了。
$x(t) = -e^{-t}u(-t) - e^{-2t}u(t)$

另外插一句确定ROC的好办法：有时候题目会说某一信号 $x(t)$ 是绝对可积之类的描述。但是，可千万别小看了“绝对可积”这个条件。他表示的含义是——这个信号的傅里叶变换存在！ 这就意味着 $x(t)$ 的ROC应该包括虚轴！！而如果恰好你的极点都是 >0 的，那么直接可以确定 ROC 平面是最左边极点的左边的。

---

二、由零极点图对傅里叶变换几何求值

这一部分的内容常常用于求解一些滤波器的幅频特性和相频特性。我们一起来看看怎么做的：

【1】首先咱们得画出零极点图。假设其极点是 $-\frac{1}{τ}$，没有零点。

【2】接下来，我们在虚轴上随便取一点，那么幅频特性就是每一个零点到虚轴这个点得向量的模值的乘积，比上所有极点到这个点向量模值的乘积，相频特性就是所有零点到该点的向量的夹角之和减去所有极点到该点的向量的夹角之和。

如上图所示，那么幅频特性就是：

相频特性为：

我们再次回到刚刚的例子：（假设其极点是 $-\frac{1}{τ}$，没有零点。）那么我们在虚轴随便取了一个点，极点到这个点的向量如下图所示：

我们可以看到，当频率从0开始逐渐增大的时候，这个向量的长度也是单调增加。（但是由于极点向量的长度是放在分母的，所以整个幅频特性的模值是单调下降的）在频率为0时，能够取得最大值。

所以在频率从0增大到正无穷时，幅频特性是从一个数开始慢慢下降，最后趋近于0.如下图所示：

在频率从0减小到负无穷时，变化是对称的。相频特性如下所示：

因此在频率为0时，角度是0.在频率是正无穷时，- $θ$ = - $\frac{π}{2}$

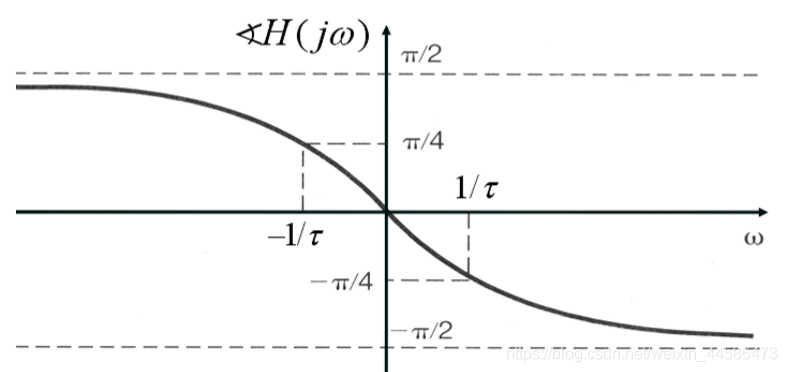
上面的是一阶系统，我们下面简单看看二阶的系统：具体的推导大家详见奥本海姆的《信号与系统》这里只给出幅频特性的大致曲线。

这样的效果我们称系统具有带通特性。

好啦！有到了本次博客结束的时候啦！本次博客我们学习了拉普拉斯反变换（尤其是部分分式展开的方法是经常要用的）另外在引言部分所提到了两组信号的拉氏变换对需要牢牢记忆。我们还研究了由零极点图对傅里叶变换几何求值。下一篇博客，我们将会探讨拉氏变换和系统性质方面的关系。See You！