傅里叶分析方法之所以在信号与LTI系统分析中如此有用,很大程度上是因为相当广泛的信号都可以表示成复指数信号的线性组合,而复指数函数是一切LTI系统的特征函数。
傅里叶变换是以复指数函数的特例和
为基底分解信号。对更一般的复指数函数
和
,也理应能以此为基底对信号进行分解。
一.拉普拉斯变换的定义
设函数,当
有定义,而且积分
![]()
s为一复数变量,成为复频率。
在 所确定的某一收敛域内收敛,则由此积分所确定的函数可以写为:

我们称上式为函数的拉普拉斯变换式,记做:

叫做
的拉氏变换。
叫做
的拉氏逆变换:

以上两式分别称为双边拉普拉斯变换和双边拉普拉斯反变换。
考虑到实际信号都是有起因信号,所以:
![]()
采用系统,相应的拉氏变换为:
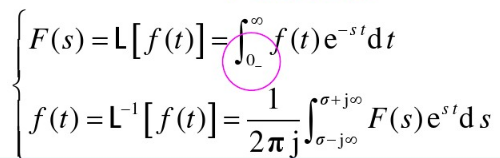
二.拉普拉斯变换的收敛域
收敛域:使存在的s的区域称为收敛域。
实际上就是拉氏变换存在的条件:

信号拉普拉斯变换的收敛域:
例:
实际上就是让
收敛,满足傅里叶变换的条件。
三.拉普拉斯变换的性质
1.线性性质

2.延时特性(时域平移)

3.尺度变换

4.复频移特性(s域平移)

5.时域微分定理


6.时域积分定理

7.s域微积分定理

8.初值定理和终值定理

9.时域卷积
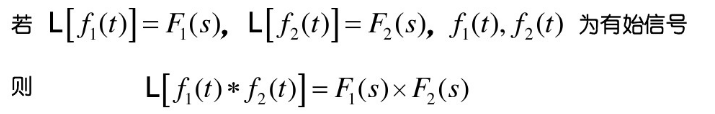
四.拉普拉斯变换的应用领域
有些情形下一个实变量函数在实数域中进行一些运算并不容易,但若将实变量函数作拉普拉斯变换,并在复数域中作各种运算,再将运算结果作拉普拉斯反变换来求得实数域中的相应结果,
在经典控制理论中,对控制系统的分析和综合,都是建立在拉普拉斯变换的基础上的。引入拉普拉斯变换的一个主要优点,是可采用传递函数代替常系数微分方程来描述系统的特性。这就为采用直观和简便的图解方法来确定控制系统的整个特性、分析控制系统的运动过程,以及提供控制系统调整的可能性。
应用拉普拉斯变换解常变量齐次微分方程,可以将微分方程化为代数方程,使问题得以解决。在工程学上,拉普拉斯变换的重大意义在于:将一个信号从时域上,转换为复频域(s域)上来表示;在线性系统,控制自动化上都有广泛的应用。
注:本文整理网上资料,包括知乎、博客等,如有侵权立刻删
