一.常数e
高等数学中的e全称为自然常数e。
1.e的由来
自然一词是指自然界的现象,是客观存在的或者说是本有的属性。比如自然数。e是人们在利息的计算中发现的一个极限的数字,因为是本身就存在。只是被人类发现了,故称之为自然常数。
2.e的计算
(1)e的精确值是没办法计算出的,因为e是无理数,是一个无限不循环小数,因此我们只能计算出他的近似值。
(2)根据高等数学中的极限公式,可以求出:当n->∞时,lim(1+1/n)^n=e
所以求e的近似值,可让n取100,1000,10000,100000等,然后利用计算机来计算。如:
3.例子
假设本金为1元,年利率为100%,
如果一年发一次利息,即一共发一次利息,那么一年后账户余额为1+1=2元。
如果半年发一次利息,即一共发两次利息,发完利息你立刻将利息存入,一年后账户余额为1+ 1/2 + (1+1/2)/2=2.25元。
现在假设每年发n次利息,则最后账户余额为:1+1/n+(1+1/n)/n+(1+1/n+(1+1/n)/n)/n+……………
如果n趋于正无穷,那么最后的结果就是e。
二.导数
导数(Derivative)是微积分中的重要基础概念。高中数学选修2-2
微积分的发明人之一是牛顿,牛顿主要还是研究物理为主,微积分不过是他发明出来研究物理的一个数学工具。
1.导数的定义
当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。
2.导数的概念
导数是函数的局部性质。通俗的讲:
(1)导数是变化率,即是曲线的切线斜率。
(2)导数是用来找到“线性近似”的数学工具。
(3)导数是线性变换。
例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
(1)什么是切线?
圆的切线我们都知道,垂直于半径就行了。一般的曲线呢?我们无法定义出一个类似“半径”的东西,然后做垂直。要知道,曲率半径是由导数定义的啊。先有了导数才有了曲率半径这种东西。
曲线上两个点确定一条割线。当两个点足够靠近的时候,割线变成了切线。
好,什么叫足够靠近?足够靠近的两个点,是一个点还是两个点?
如果是两个点,这还是割线。如果是一个点,那直线是怎么画出来的?
(2)导数的诞生
于是人们陷入了困惑。然而,“极限”思想出现了。这时候人们从另一条路去考虑切线的问题。
人们慢慢接受了用ε-δ语言,去理解“无穷小”,“无限接近”等概念。我们可以理解成这样:
一条曲线的割线,总是有斜率的。固定住一个点,让另一个点去靠近它,这时候斜率在发生变化。
但是这些斜率有一个特点,就是它们可以在两个点越来越近的时候,越来越接近一个数值。这个数值就是【导数】。
注意:切线是算出来的,不是画出来的。
3.可导函数的定义
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
对于可导的函数f(x),x↦f'(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。反之,已知导函数也可以倒过来求原来的函数,即不定积分。微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作,它们都是微积分学中最为基础的概念。
4.导数的计算:
(1)列举几个基本初等函数的导数:
(2)导数的求导法则:
导数的四则运算:
……………….①
………………②
………………③
- 求导的线性:对函数的线性组合求导,等于先对其中每个部分求导后再取线性组合(即①式)。
- 两个函数的乘积的导函数:一导乘二+一乘二导(即②式)。
- 两个函数的商的导函数也是一个分式:(子导乘母-子乘母导)除以母平方(即③式)。
- 如果有复合函数,则用链式法则求导。
(3)导数的高阶求导:
&& 直接法:由高阶导数的定义逐步求高阶导数。一般用来寻找解题方法。
&& 高阶导数的运算法则:
(二项式定理)
&& 间接法:利用已知的高阶导数公式,通过四则运算,变量代换等方法。
注意:代换后函数要便于求,尽量靠拢已知公式求出阶导数。
5.导数的应用场景
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为优化问题,通过学习,我们知道,导数是求函数最大(小)值的有力工具。导数的实际应用
三.梯度
1.梯度的定义
梯度可谓是多元函数中一个基本的名词。梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。方向指向数值增长最快的方向,大小为变化率。
在向量微积分中,标量场的梯度是一个向量场。标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
总结:在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜率。
梯度一词有时用于斜度,也就是一个曲面沿着给定方向的倾斜程度。可以通过取向量梯度和所研究的方向的点积来得到斜度。梯度的数值有时也被成为梯度。
2.梯度与导数的关系
通过梯度的定义我们发现,梯度的求解其实就是求函数偏导的问题。
梯度是矢量而某点的导数是个常量,两者应该有本质的区别,而导数的正负也反映了函数值的大小变化,而不是一直指向数值增大的方向。
在此我们通过一张图来说明解释一下两者的关系:
3.梯度的计算
梯度下降法
四.Taylor
1.泰勒公式的定义
数学中,泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数足够平滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了这个多项式和实际的函数值之间的偏差。
2.泰勒公式的应用
计算机不会计算三角函数,复杂对数函数,复杂指数函数,但是要计算这些函数怎么办?我们可以转化为计算机能够计算的且值非常近似公式,泰勒公式就是将复杂函数转化为计算机可以计算的形式。计算机无法对三角函数,对数函数,直接计算,而泰勒公式可以将所有的复杂函数转化为简单的加减乘除的近似运算,从而利用计算机进行计算,减少了人工计算的复杂度,进而在物理,化学,材料,航天.......等工程领域广泛应用。
3.泰勒公式的推导
(1)泰勒公式展开式
泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。
若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶导数,且在开区间(a,b)上具有(n+1)阶导数,则对闭区间[a,b]上任意一点x,成立下式:

其中,表示f(x)的n阶导数,等号后的多项式称为函数f(x)在x0处的泰勒展开式,剩余的Rn(x)是泰勒公式的余项,是(x-x0)n的高阶无穷小。
(2)麦克劳林公式
函数的麦克劳林展开指上面泰勒公式中x0取0的情况,即是泰勒公式的特殊形式,若f(x)在x=0处n阶连续可导,则下式成立:

其中表示f(x)的n阶导数。
当其中δ在0与x之间时,公式称为拉格朗日型余项的n阶麦克劳林公式;
当时公式称为带佩亚诺型余项的n阶麦克劳林公式。
五.gini系数
1.基尼系数的定义
基尼系数(Gini coefficient),或称洛伦茨系数。基尼系数是指国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标。基尼系数介于0-1之间,基尼系数越大,表示不平等程度越高。它是根据洛伦茨曲线找出了判断分配平等程度的指标(如下图)。基尼系数概念
2.基尼系数的计算公式
设实际收入分配曲线和收入分配绝对平等曲线之间的面积为A,实际收入分配曲线右下方的面积为B。并以A除以A+B的商表示不平等程度。这个数值被称为基尼系数或称洛伦茨系数。如果A为零,基尼系数为零,表示收入分配完全平等;如果B为零则系数为1,收入分配绝对不平等。该系数可在零和1之间取任何值。收入分配越是趋向平等,洛伦茨曲线的弧度越小,基尼系数也越小,反之,收入分配越是趋向不平等,洛伦茨曲线的弧度越大,那么基尼系数也越大。如果个人所得税能使收入均等化,那么,基尼系数即会变小。
基尼系数的计算公式为:
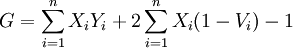
其中,X代表各组的人口比重,Y代表各组的收入比重,V代表各组累计的收入比重,i=1,2,3,…,n,n代表分组的组数。
基尼系数,按照联合国有关组织规定:
- 若低于0.2表示收入绝对平均;
- 0.2-0.3 表示比较平均;
- 0.3-0.4 表示相对合理;
- 0.4-0.5 表示收入差距较大;
- 0.5 以上表示收入差距悬殊。
经济学家们通常用基尼指数来表现一个国家和地区的财富分配状况。这个指数在零和一之间,数值越低,表明财富在社会成员之间的分配越均匀;反之亦然。
通常把0.4作为收入分配差距的“警戒线”。一般发达国家的基尼指数在0.24到0.36之间,美国偏高,为0.4。中国大陆和香港的基尼系数都超出0.4。
此外洛伦茨曲线讲的是市场总发货值的百分比与市场中由小到大厂商的累积百分比之间的关系。 洛伦茨曲线的弧度越小,基尼系数也越小。
六.信息熵
1.信息熵的定义
信息是个很抽象的概念。人们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信息量。 信息熵是对信息的量化。
2.信息熵的理解
一个事件或一个系统,准确的说是一个随机变量,它有着一定的不确定性。例如,“除东道主俄罗斯外,哪31个国家能进军2018年俄罗斯世界杯决赛圈”,这个随机变量的不确定性很高,要消除这个不确定性,就需要引入很多的信息,这些很多信息的度量就用“信息熵”表达。需要引入消除不确定性的信息量越多,则信息熵越高,反之则越低。例如“中国男足进军2018年俄罗斯世界杯决赛圈”,这个因为确定性很高,几乎不需要引入信息,因此信息熵很低。
信息熵是消除不确定性所需信息量的度量,也即未知事件可能含有的信息量。
3.信息熵的计算
根据香农(Shannon)给出的信息熵公式,对于任意一个随机变量X,它的信息熵定义如下,单位为比特(bit):
H(X)=−∑xεXP(x)logP(x))
H(X)=−∑xεXP(x)logP(x))
那么上述随机变量(谁获得冠军)的信息量是:
H=-(p1·logp1+p2·logp2+…p32·logp32)
其中,p1,p2,…,p32分别是这32强球队夺冠的概率。
给出了几个结论:一是32强球队夺冠概率相同时,H=5;二是夺冠概率不同时,H<5;三是H不可能大于5。
对于第一个结论:结果是很显然的,夺冠概率相同,即每个球队夺冠概率都是1/32,所以H=-((1/32)·log(1/32)+(1/32)·log(1/32)+…+(1/32)·log(1/32))=-log(1/32)=log(32)=5(bit)
对于第二个结论和第三个结论:使用拉格朗日乘子法进行证明,详见《求约束条件下极值的拉格朗日乘子法》。这实际上是说系统中各种随机性的概率越均等,信息熵越大,反之越小。
从香农给出的数学公式上可以看出,信息熵其实是一个随机变量信息量的数学期望。
4.信息熵的应用
信息熵的一个重要应用领域就是自然语言处理。例如,一本50万字的中文书平均有多少信息量。我们知道,常用的汉字约7000字。假如每个汉字等概率,那么大约需要约13比特(即13位二进制数,213213=8192)表示一个汉字。
应用信息熵就是,一个汉字有7000种可能性,每个可能性等概率,所以一个汉字的信息熵是:
H=-((1/7000)·log(1/7000)+(1/7000)·log(1/7000)+…(1/7000)·log(1/7000))=12.77(bit)
实际上由于前10%汉字占常用文本的95%以上,再考虑词语等上下文,每个汉字的信息熵大约是5比特左右。所以一本50万字的中文书,信息量大约是250万比特。需要注意这里的250万比特是个平均数。
再看下面两个句子:
(1)落霞与孤鹜齐飞,秋水共长天一色。
(2)落日下的晚霞与孤独的大雁一同飞翔,晚秋的江水和深远的天空连成一片。
按照信息熵的计算,第二句比第一句的信息熵要高1倍以上,你会觉得第二句比第一句水平要高,信息量更大么?在自然语言处理中出现较大的信息熵,只表示可能出现的语言字符较多,并不意味着你可以从中得到更多的信息。
所以,信息熵高,不代表你说的话,写的文字中蕴含的信息量就比别人高了。更确切的,信息熵在自然语言处理中是用来对语言文字进行数据压缩的,与语言素养无关。当然条件熵、相对熵等应该是自然语言处理中更有用的概念。
在自然语言处理中,信息熵只反映内容的随机性(不确定性)和编码情况,与内容本身无关。
七.组合数
1.组合数的定义
组合是数学的重要概念之一。从 n 个不同元素中每次取出 m 个不同元素 ,不管其顺序合成一组,称为从 n 个元素中不重复地选取 m 个元素的一个组合。所有这样的组合的种数称为组合数。
,不管其顺序合成一组,称为从 n 个元素中不重复地选取 m 个元素的一个组合。所有这样的组合的种数称为组合数。
2.排列组合的概念
排列组合是组合学最基本的概念。所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。排列组合的应用
3.组合数的计算
在线性写法中被写作C(n,m)。组合数的计算公式为:

n 元集合 A 中不重复地抽取 m 个元素作成的一个组合实质上是 A 的一个 m 元子集和。如果给集 A 编序

成为一个序集,那么 A 中抽取 m 个元素的一个组合对应于数段

到序集 A 的一个确定的严格保序映射。组合数 的常用符号还有
的常用符号还有

八.梯度下降法和牛顿法
1.常见的几种最优化方法
我们每个人都会在我们的生活或者工作中遇到各种各样的最优化问题,比如每个企业和个人都要考虑的一个问题“在一定成本下,如何使利润最大化”等。最优化方法是一种数学方法,它是研究在给定约束之下如何寻求某些因素(的量),以使某一(或某些)指标达到最优的一些学科的总称。随着学习的深入,博主越来越发现最优化方法的重要性,学习和工作中遇到的大多问题都可以建模成一种最优化模型进行求解,比如我们现在学习的机器学习算法,大部分的机器学习算法的本质都是建立优化模型,通过最优化方法对目标函数(或损失函数)进行优化,从而训练出最好的模型。常见的最优化方法有梯度下降法、牛顿法和拟牛顿法、共轭梯度法等等。
2.梯度下降法
梯度下降法是最早最简单,也是最为常用的最优化方法。梯度下降法实现简单,当目标函数是凸函数时,梯度下降法的解是全局解。一般情况下,其解不保证是全局最优解,梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以也被称为是”最速下降法“。最速下降法越接近目标值,步长越小,前进越慢。因为梯度的方向就是函数之变化最快的方向。梯度下降法及其实现
3.牛顿法
牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。
具体步骤:
首先,选择一个接近函数 f (x)零点的 x0,计算相应的 f (x0) 和切线斜率f ' (x0)(这里f ' 表示函数 f 的导数)。然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和 x 轴的交点的x坐标,也就是求如下方程的解:

我们将新求得的点的 x 坐标命名为x1,通常x1会比x0更接近方程f (x) = 0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示:
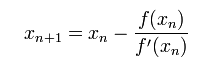
已经证明,如果f ' 是连续的,并且待求的零点x是孤立的,那么在零点x周围存在一个区域,只要初始值x0位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果f ' (x)不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。下图为一个牛顿法执行过程的例子。
由于牛顿法是基于当前位置的切线来确定下一次的位置,所以牛顿法又被很形象地称为是"切线法"。





