a## draw line
给定(x0,y0) (x1,y1)两个点,画出一条直线。 首先通过交换x,y轴使得变化较快的那个轴变为x轴,再交换x0,x1使得x1永远大于x0。令dx=x1-x0;dy=y1-y0;
从(x0,y0)开始,x轴每增加一个像素,因为y轴变化较慢所以增加的值dy/dx小于1, 把增加的值累积起来用变量error记录,每当error>0.5就令y的值增加1,同时error的值减去1. 但是这样做的缺点是需要使用0.5和dy/dx两个浮点数,所以直接两者同时乘以2dx。
void line(int x0, int y0,int x1, int y1, TGAImage &image,TGAColor color){
bool steep=false;
if(abs(y1-y0)>abs(x1-x0)){
steep=true;
std::swap(x0,y0);
std::swap(x1,y1);
}
if(x1<x0){
std::swap(x0,x1);
std::swap(y0,y1);
}
int dx=x1-x0;
int dy=y1-y0;
int derror=abs(dy)*2;
int error=0;
for(int x=x0, y=y0;x<=x1;x++){
error+=derror;
if(error>dx){
y+=dy>0?1:-1;
error-=2*dx;
}
if(steep){
image.set(y,x, color);
}else{
image.set(x,y,color);
}
}
}
-
模型导入
.obj文件的每一行要么是点,要么表示一个面v 0.296 -0.070 0.953 v -0.319 -0.065 0.946
f 1193/1240/1193 1180/1227/1180 1179/1226/1179
第一行表示一个点,使用归一化坐标,第二行表示由第1193,1180和1179个点组成的面。这些序号都是从1开始。
triangle
思路,求出三角形的bbox后,需要判断其中的每一个点是否在三角形内。 这里用到了重心坐标的概念,即如果P在三角形ABC内,则存在三个分别放在ABC点上的质量,使得P成为三角形的重心。
即P点满足
u P A → + v P B → + ( 1 − u − v ) P C → = 0 u \overrightarrow{P A}+v \overrightarrow{P B}+(1-u-v) \overrightarrow{PC}=0 uPA+vPB+(1−u−v)PC=0
现在给定P点需要求出u,v,(1-u-v),如果其中一个值小于0则说明P不在三角形内。
整理得
{ [ u v 1 ] [ C A → x C B → x P C → x ] = 0 [ u v 1 ] [ C A → y C B → y P C → y ] = 0 \left\{\begin{array}{l} {\left[\begin{array}{lll} u & v & 1 \end{array}\right]} & {\left[\begin{array}{c} \overrightarrow{CA}_{x} \\ \overrightarrow{CB}_{x} \\ \overrightarrow{P C}_{x} \end{array}\right]=0} \\ {\left[\begin{array}{lll} u & v & 1 \end{array}\right]} & {\left[\begin{array}{c} \overrightarrow{CA}_{y} \\ \overrightarrow{CB}_{y} \\ \overrightarrow{PC}_{y} \end{array}\right]=0} \end{array}\right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧[uv1][uv1]⎣⎢⎢⎡CAxCBxPCx⎦⎥⎥⎤=0⎣⎢⎢⎡CAyCByPCy⎦⎥⎥⎤=0
可以看出(u,v,1)和两个向量(ABx,ACx,PAx) and (ABy,ACy,PAy)正交,所以可以先求出两个向量的叉乘,然后除以z轴的值,得到(u,v,1),注意这里叉乘结果的z值可能为0,这种情况可以直接归为P不在三角形内。
Vec3f barycentric(Vec2i* pts,Vec2i P){
Vec3i v1(pts[1].x-pts[0].x,pts[2].x-pts[0].x,pts[0].x-P.x);
Vec3i v2(pts[1].y-pts[0].y,pts[2].y-pts[0].y,pts[0].y-P.y);
auto u=v1.cross(v2);
if(u.z==0){
return Vec3f(-1,1,1);
}else{
Vec3f v=u;
return Vec3f(v.x/v.z,v.y/v.z,1.0f-(v.x+v.y)/v.z);
}
}
void triangle(Vec2i* pts, TGAImage& image,TGAColor color){
Vec2i boxmax(0,0);
Vec2i boxmin(image.get_width()-1,image.get_height()-1);
for(int i=0;i<3;i++){
for(int j=0;j<2;j++){
if(pts[i].raw[j]>boxmax.raw[j]){
boxmax.raw[j]=pts[i].raw[j];
}
if(pts[i].raw[j]<boxmin.raw[j]){
boxmin.raw[j]=pts[i].raw[j];
}
}
}
for(int x=boxmin.x;x<=boxmax.x;x++){
for(int y=boxmin.y;y<=boxmax.y;y++){
Vec2i P(x,y);
auto b= barycentric(pts,P);
if(b.x>=0 && b.y>=0&& b.z>=0){
image.set(x,y,color);
}
}
}
}
坑点:注意u,v和x,y,z的对应关系。
Zbuffer
上面的实现的triangle没有考虑深度的问题,即使三角形A的z值比三角形B大,但是渲染时还是可能被B给覆盖,解决方法是利用一个zbuffer[image_width*imag_height],来缓存渲染过程中,三角形上每个点的z值,这样渲染结束后,zbuffer中每一个z值都是所有对应点中最大的。 三角形上某点z值的计算过程是以该点的重心坐标为权重,乘以三角形三个顶点的z坐标。
void triangle(Vec3i* pts, float* z_buffer, TGAImage& image,TGAColor color){
Vec2i boxmax(0,0);
Vec2i boxmin(image.get_width()-1,image.get_height()-1);
for(int i=0;i<3;i++){
for(int j=0;j<2;j++){
if(pts[i].raw[j]>boxmax.raw[j]){
boxmax.raw[j]=pts[i].raw[j];
}
if(pts[i].raw[j]<boxmin.raw[j]){
boxmin.raw[j]=pts[i].raw[j];
}
}
}
for(int x=boxmin.x;x<=boxmax.x;x++){
for(int y=boxmin.y;y<=boxmax.y;y++){
Vec2i P(x,y);
auto b= barycentric(pts,P);
if(b.x>=0 && b.y>=0&& b.z>=0){
float z=0;
for(int i=0;i<3;i++){
z+=b.raw[i]*pts[i].z;
}
int index=P.y*image.get_width()+P.x;
if(z_buffer[index]<z){
z_buffer[index]=z;
image.set(x,y,color);
}
}
}
}
}
projection texture
v 0.296 -0.070 0.953 v -0.319 -0.065 0.946
f 1193/1240/1193 1180/1227/1180 1179/1226/1179
第二行除了表示由第1193,1180和1179个点组成的面之外,还表示三个顶点分别对应第1240,1227,1226个uv坐标点(vt)和第1193,1189,1179个法向量点(vn)。
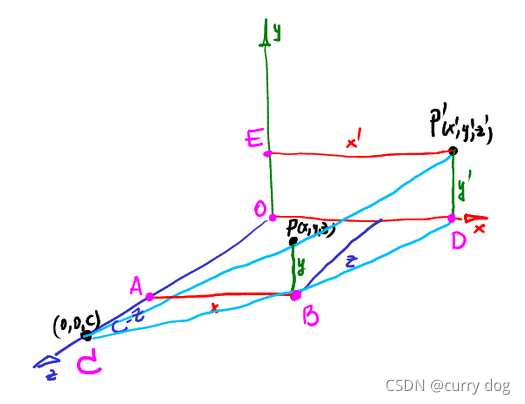
和视觉里的相机模型不同,这里原点在像平面上,假设相机坐标为(0,0,c), 那么物体上某点在像平面上的投影坐标可以用下式计算:
[ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 − 1 / c 1 ] [ x y z 1 ] = [ x y z 1 − z / c ] \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & -1 / c & 1 \end{array}\right]\left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right]=\left[\begin{array}{c} x \\ y \\ z \\ 1-z / c \end{array}\right] ⎣⎢⎢⎡10000100001−1/c0001⎦⎥⎥⎤⎣⎢⎢⎡xyz1⎦⎥⎥⎤=⎣⎢⎢⎡xyz1−z/c⎦⎥⎥⎤
计算投影矩阵的函数一般以1/c为参数,因为可以令1/c为0,这样就等于正射投影。
相机移动需要提供三个参数,一个是相机的位置eye,一个是目标点center,即新的坐标系原点,以及up向量。up向量在像平面的投影就是新的y轴。由center到eye的向量就是新的z轴方向。利用新z轴和up的叉乘可以得到新的x轴方向,最后用z和x的叉乘可以得到新y轴方向。
新坐标系下的坐标 x ′ , y ′ , z ′ x^{\prime},y^{\prime},z^{\prime} x′,y′,z′可以用下式计算
[ x y z ] = [ O x ′ O y ′ O z ′ ] + M [ x ′ y ′ z ′ ] ⇒ [ x ′ y ′ z ′ ] = M − 1 ( [ x y z ] − [ O x ′ O y ′ O z ′ ] ) \left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\left[\begin{array}{l} O_{x}^{\prime} \\ O_{y}^{\prime} \\ O_{z}^{\prime} \end{array}\right]+M\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{array}\right] \quad \Rightarrow \quad\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{array}\right]=M^{-1}\left(\left[\begin{array}{l} x \\ y \\ z \end{array}\right]-\left[\begin{array}{c} O_{x}^{\prime} \\ O_{y}^{\prime} \\ O_{z}^{\prime} \end{array}\right]\right) ⎣⎡xyz⎦⎤=⎣⎡Ox′Oy′Oz′⎦⎤+M⎣⎡x′y′z′⎦⎤⇒⎣⎡x′y′z′⎦⎤=M−1⎝⎛⎣⎡xyz⎦⎤−⎣⎡Ox′Oy′Oz′⎦⎤⎠⎞
其中M矩阵是新坐标系三个轴对应的向量组成标准正交基。 O ′ O^{\prime} O′是给定的center点的坐标。
在视角变换,投影变换之前,模型的坐标值在定义域 [ − 1 , 1 ] ∗ [ − 1 , 1 ] ∗ [ − 1 , 1 ] [-1,1]*[-1,1]*[-1,1] [−1,1]∗[−1,1]∗[−1,1] 中,需要利用viewport矩阵将转换后的定义域变为 [ x , x + w ] ∗ [ y , y + h ] ∗ [ 0 , d ] [x,x+w]*[y,y+h]*[0,d] [x,x+w]∗[y,y+h]∗[0,d],这里d一般设置为255,方便将zbuffer映射为一个图片:
[ w 2 0 0 x + w 2 0 h 2 0 y + h 2 0 0 d 2 d 2 0 0 0 1 ] \left[\begin{array}{cccc} \frac{w}{2} & 0 & 0 & x+\frac{w}{2} \\ 0 & \frac{h}{2} & 0 & y+\frac{h}{2} \\ 0 & 0 & \frac{d}{2} & \frac{d}{2} \\ 0 & 0 & 0 & 1 \end{array}\right] ⎣⎢⎢⎡2w00002h00002d0x+2wy+2h2d1⎦⎥⎥⎤
直接对法向量进行变换的结果不一定正确(当变换矩阵为正交矩阵是可以直接对法向量变换)。假设变换前法向量为[A,B,C,0](在齐次坐标系中,向量的最后一维为0), 它对应一个平面,对平面上任何点(x,y,z)都有
[ A B C 0 ] × [ x y z 1 ] = 0 \left[\begin{array}{llll} A & B & C & 0 \end{array}\right] \times\left[\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right]=0 [ABC0]×⎣⎢⎢⎡xyz1⎦⎥⎥⎤=0
在上式中间插入单位矩阵 M − 1 M M^{-1}M M−1M得到
( [ A B C 0 ] × M − 1 ) × ( M × [ x y z 1 ] ) = 0 \left(\left[\begin{array}{llll} A & B & C & 0 \end{array}\right] \times M^{-1}\right) \times\left(M \times\left[\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right]\right)=0 ([ABC0]×M−1)×⎝⎜⎜⎛M×⎣⎢⎢⎡xyz1⎦⎥⎥⎤⎠⎟⎟⎞=0
整理得
( ( M ⊤ ) − 1 × [ A B C 0 ] ) ⊤ × ( M × [ x y z 1 ] ) = 0 \left(\left(M^{\top}\right)^{-1} \times\left[\begin{array}{l} A \\ B \\ C \\ 0 \end{array}\right]\right)^{\top} \times\left(M \times\left[\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right]\right)=0 ⎝⎜⎜⎛(M⊤)−1×⎣⎢⎢⎡ABC0⎦⎥⎥⎤⎠⎟⎟⎞⊤×⎝⎜⎜⎛M×⎣⎢⎢⎡xyz1⎦⎥⎥⎤⎠⎟⎟⎞=0
可以发现右边正好是变换后的(x,y,z)点。所以应该对法向量进行的变换是 ( M ⊤ ) − 1 \left(M^{\top}\right)^{-1} (M⊤)−1
- 注意:我们真正关心的重心坐标是根据三维空间中的顶点得到的,而不是根据投影到屏幕上的点得到的,但是对三角形进行采样时必须使用屏幕坐标,可以通过修正算法将屏幕上的重心坐标变成三维空间中的重心坐标:
z P = 1 a z A + b z B + c z C I P = ( a I A z A + b I B z B + c I C z C ) / 1 z P \begin{gathered} z_{P}=\frac{1}{\frac{a}{z_{A}}+\frac{b}{z_{B}}+\frac{c}{z_{C}}} \\ I_{P}=\left(a \frac{I_{A}}{z_{A}}+b \frac{I_{B}}{z_{B}}+c \frac{I_{C}}{z_{C}}\right) / \frac{1}{z_{P}} \end{gathered} zP=zAa+zBb+zCc1IP=(azAIA+bzBIB+czCIC)/zP1
其中a,b,c是根据屏幕上的点得到的重心坐标,z是三维空间的深度,I是某个属性值
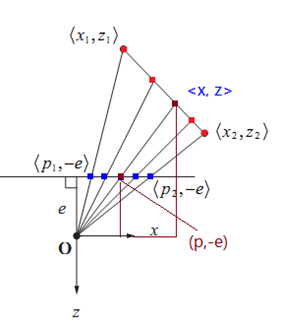
这个原理是,假设三维空间点(x,y,z)的投影点为 ( P x , P y , 0 ) (P_{x},P_{y},0) (Px,Py,0),根据投影矩阵可得
x = ( P x C − P x z ) / C x=(P_{x} C-P_{x} z)/C x=(PxC−Pxz)/C 同理可得y的表示方法,代入三维空间中的平面方程可以发现 1 / z 1/z 1/z可以用 P x P_{x} Px, P y P_{y} Py线性表示,所以在投影平面的插值也可以应用到 1 / z 1/z 1/z上
这里的光照模型比较简单,由漫反射diffuse和全反射specular组成,前者用法向量n和入射光线l的内积表示,而后者由反射光线r的z值表示,这里的z轴指的就是由相机指向原点的轴,所以要求以上所有的方向向量全部都是经过了变换之后的:
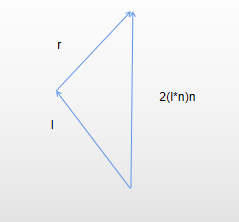
这里入射光线是远离物体的。
alpha 是当前待绘制颜色和缓冲区颜色的混合系数,alpha越接近1越不透明。
不翻转的话,屏幕的y轴向下,物体坐标系的y轴往物体上方 纹理图本身的y轴向下
不管模型坐标系中,x指向左边还是右边,y轴指向上面还是下面,只要把该轴作为up向量,那么它在屏幕中都指向上方。深度测试优先显示z值大即离相机近的点。
-
实现
着色器分为两个部分,vertex和fragment,前者负责计算三角形顶点的坐标,以及获取对应的uv坐标,每个面对应的所有uv坐标缓存在shader中,方便fragment使用。 fragment负责根据当前内部点的重心坐标获取颜色信息。两者每次都只负责处理一个点。struct MyShader : public IShader{ explicit MyShader(Model*m){ M=ViewPort*Projection*ModelView; invertTransposeM=M.invert_transpose(); model=m; } Vec4f vertex(int fid,int nthVertex) override{ Vec4f vert=proj<4>(model->vert(fid,nthVertex),1.0f); originPts.set_col(nthVertex,vert); vert=ViewPort*Projection*ModelView*vert; varying_uv.set_col(nthVertex,model->uv(fid,nthVertex)); return vert; } bool fragment(Vec3f bar,TGAColor& color) override{ Vec2f uv=varying_uv*bar; Vec3f n= proj<3,float>(invertTransposeM*proj<4,float>(model->normal(uv)),0).normalize(); Vec3f l=proj<3,float>(M*proj<4,float>(light_dir),0).normalize(); float diff=std::max(0.f, n*l); Vec3f r= (n*(n*l*2.f) - l).normalize().normalize(); float spec=pow(std::max(0.f,r.z),model->specular(uv)); auto c=model->diffuse(uv); for(int i=0;i<3;i++){ color.raw[i]=std::min<float>(5+c.raw[i]*(diff+spec),255); } return true; } };求矩阵的逆,需要分解为求矩阵的伴随矩阵adjugate和求行列式,而求伴随矩阵相当于求每个元素的余子式cofactor,而求余子式又需要求出低阶的行列式。所以整个过程可以看成是cofactor函数和det函数的递归调用,这里用模板的特化来终止递归。
template<size_t DimCols,size_t DimRows,typename T> class mat; template<size_t DIM,typename T> struct dt { static T det(const mat<DIM,DIM,T>& src) { T ret=0; for (size_t i=DIM; i--; ret += src[0][i]*src.cofactor(0,i)); return ret; } }; template<typename T> struct dt<1,T> { static T det(const mat<1,1,T>& src) { return src[0][0]; } }; mat<DimRow-1,DimCol-1,T> get_minor(int row, int col) const{ mat<DimRow-1,DimCol-1,T> ret; for(int i=0;i<DimRow-1;i++){ for(int j=0;j<DimCol-1;j++){ ret[i][j]= rows_[i>=row?i+1:i][j>=col?j+1:j]; } } return ret; } T cofactor(int row,int col) const{ return (get_minor(row,col).det())*((row+col)%2?-1:1); } T det() const{ return dt<DimCol,T>::det(*this); } mat<DimRow,DimCol,T> adjugate(){ mat<DimRow,DimCol,T> ret; for(int i=0;i<DimRow;i++){ for(int j=0;j<DimCol;j++){ ret[i][j]= cofactor(i,j); } } return ret; }坑点:法向量贴图在读取时要注意变换成[-1,1], 在做深度测试时要对z值进行裁剪z= std::max(0, std::min(255, int(z+.5)));

-
tangent space
之前的法向量贴图是建立在对象空间上的,如果想把纹理用到其它模型上就不行了,而建立在切线空间上的法向量贴图可以用在不同的模型上。
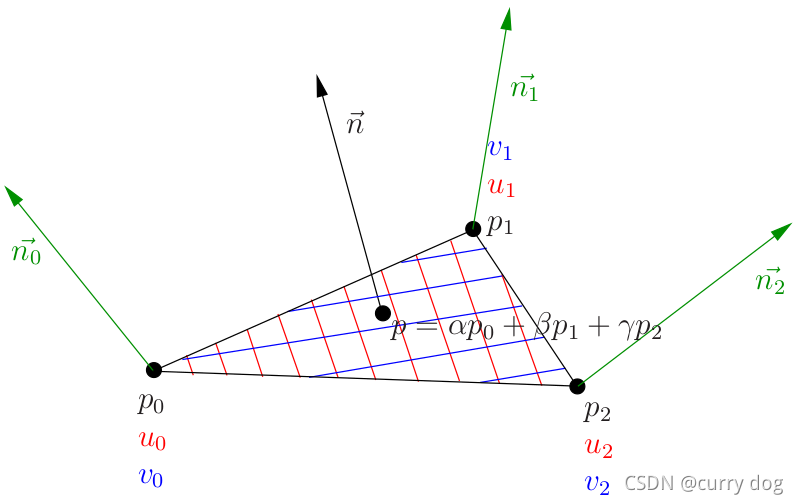
有了切线坐标系后,从法向量纹理图中读取的就是在切线坐标系中的坐标值。 在切线坐标系中,z的值永远大于0并且在[0.1]之间,其它两轴在[-1,1]之间,用(normal + 1) / 2*255 转换成RGB格式保存到文件中,可以看出由于z大于0所以轴对应的blue通道总是大于255/2,所以切线纹理图像中出现大片蓝色。
三角形上每一个点都有自己的切向量空间,它的x轴(T)就是当前点u变化最快的方向,y轴(B)是纹理坐标v变化最快的方向,z轴(N)可以是插值得到的法向量方向。
以求T为例,假设u是顶点坐标的线性函数Ax+By+Cz+D那么其变化最快的方向就是梯度(A,B,C), 它的解法为:
{ p 0 p 1 → ⋅ ( A B C ) = f 1 − f 0 p 0 p 2 → ⋅ ( A B C ) = f 2 − f 0 n → ⋅ ( A B C ) = 0 \left\{\begin{array}{rl} \overrightarrow{p_{0} p_{1}} & \cdot(A & B & C) & =f_{1}-f_{0} \\ \overrightarrow{p_{0} p_{2}} & \cdot(A & B & C) & =f_{2}-f_{0} \\ \overrightarrow{n} & \cdot (A & B & C) & =0 \end{array}\right. ⎩⎨⎧p0p1p0p2n⋅(A⋅(A⋅(ABBBC)C)C)=f1−f0=f2−f0=0
实际上这样求出来的三个轴不一定正交,所以可以先求出u的梯度作为T,然后和v的梯度叉乘得到N轴,最后NxT得到B轴.
沿着任意方向变化时的导数,可以看出梯度方向时,变化最快
D u f ( x , y ) = f x ( x , y ) cos θ + f y ( x , y ) sin θ D_{u} f(x, y)=f_{x}(x, y) \cos \theta+f_{y}(x, y) \sin \theta Duf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ
bool fragment(Vec3f bar,TGAColor& color) override{
Vec2f uv=varying_uv*bar;
Vec3f n=(tri_normals*bar).normalize();
mat<3,3,float> A;
A[0]=tri_vertexes.get_col(1)-tri_vertexes.get_col(0);
A[1]=tri_vertexes.get_col(2)-tri_vertexes.get_col(0);
A[2]=n;
A=A.invert();
Vec3f bu(varying_uv[0][1]-varying_uv[0][0],varying_uv[0][2]-varying_uv[0][0],0);
Vec3f bv(varying_uv[1][1]-varying_uv[1][0],varying_uv[1][2]-varying_uv[1][0],0);
auto T=(A*bu).normalize();
auto B=(A*bv).normalize();
mat<3,3,float> cord;
cord.set_col(0,T);
cord.set_col(1,B);
cord.set_col(2,n);
auto read_n=model->normal(uv);
n=(cord*read_n).normalize();
float diff=std::max(0.f, n*light_dir);
Vec3f r= (n*(n*light_dir*2.f) - light_dir).normalize();
float spec=pow(std::max(0.f,r.z),model->specular(uv));
auto c=model->diffuse(uv);
for(int i=0;i<3;i++){
color.raw[i]=std::min<float>(c.raw[i]*(diff+spec),255);
// color.raw[i]=std::min<float>((diff+spec)*255,255);
}
return true;
}
};
上面所有的向量和顶点都统一只经过了projection和modelview。

shadow
这里引入了视锥的概念,并且相机点为原点。原因是我们想在三维空间内找到一个感兴趣的空间,这个空间内的点可以尽可能的填充屏幕。
视锥有近平面n和远平面f,近平面相当于像平面, 所以近平面上所有点的齐次坐标在经过透视投影后不变,远平面的中心点(0,0,f,1)经过透视投影后不变。 这两个性质保证这是一个过原点的视锥。
所以可以得到投影矩阵
n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 \begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -n f \\ 0 & 0 & 1 & 0 \end{array} n0000n0000n+f100−nf0
然后视锥被压缩成一个长方体[l,r][b,t][f,n],然后可以用正交投影装换成正方体[-1,1][-1,1][-1,1]
M ortho = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] M_{\text {ortho }}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right] Mortho =⎣⎢⎢⎡r−l20000t−b20000n−f200001⎦⎥⎥⎤⎣⎢⎢⎡100001000010−2r+l−2t+b−2n+f1⎦⎥⎥⎤
模拟阴影的思路是将相机移动到光源方向(C1坐标系),渲染然后计算shadow_buffer, 在正常渲染时(C2坐标系),把当前点变换到C1坐标系,然后比较它的z值和shadow_buffer中的z值,如果小于说明该点在光源方向被遮挡。 已知屏幕上的点(带z值),因为齐次坐标的尺度不变性,可以通过乘以变换矩阵的逆矩阵得到空间点的准确坐标。
-
精度问题
经过变换后的空间称为NDC(除以第四维w),变换前为viewspace,如果NDC中近平面为0,远平面为1,用浮点数来保存NDC中的深度值时,1附近保存了大量的远点,而浮点数靠近1时的精度反而不如靠近0的精度,所以一般令近平面为1,远平面为0.
另一方面,在像素平面上,同一块面积,能包含的远点比近点要多得多,所以像素点移动一格可能对应两个隔得非常远的远点。 因此远点的贴图一般会用高斯卷积核进行模糊。在把C2中的坐标转到光源坐标并利用深度测试来判断是否遮挡时,可以把当前点的z值加上一个常数,以减少z-fighting的情况。 -
透视修正
前面只修复了z值,并没有修复重心坐标。 前面得到z的导数是线性插值,又
因为其它变换前的属性和z值成线性关系:
a m + b z = c a m^{}+b z^{}=c am+bz=c
所以属性值除以z也是线性插值
a m c z + b c = 1 z \frac{a m^{}}{c z^{}}+\frac{b}{c}=\frac{1}{z^{}} czam+cb=z1
因此已知三个顶点投影前的z值,以及属性值,可以求得中间某点经过修正后的属性值:
u v n = Z n ( 1 − u − v Z 1 u v 1 + u Z 2 u v 2 + v Z 3 u v 3 ) u v_{n}=Z_{n}\left(\frac{1-u-v}{Z_{1}} u v_{1}+\frac{u}{Z_{2}} u v_{2}+\frac{v}{Z_{3}} u v_{3}\right) uvn=Zn(Z11−u−vuv1+Z2uuv2+Z3vuv3)
其中 Z n = 1 1 − u − v Z 1 + u Z 2 + v Z 3 Z_{n}=\frac{1}{\frac{1-u-v}{Z_{1}}+\frac{u}{Z_{2}}+\frac{v}{Z_{3}}} Zn=Z11−u−v+Z2u+Z3v1
struct MyShader : public IShader{
Mat4f otherM;
Mat4f shadowM;
float * shadowBuffer;
explicit MyShader(Model*m,float * buffer,Mat4f otherTransM):IShader(m),otherM(otherTransM)
,shadowBuffer(buffer){
M=Projection*ModelView;
invertTransposeM=M.invert_transpose();
shadowM=otherM*(M.invert());
}
Vec4f vertex(int fid,int nthVertex) override{
Vec4f vert=proj<4>(model->vert(fid,nthVertex),1.0f);
originPts.set_col(nthVertex,vert);
vert=M*vert;
varying_uv.set_col(nthVertex,model->uv(fid,nthVertex));
tri_vertexes.set_col(nthVertex, vert/vert[3]);
tri_normals.set_col(nthVertex, proj<3,float>(invertTransposeM* proj<4,float>(model->normal(fid,nthVertex),0.0f)));
return ViewPort*vert;
}
bool fragment(Vec3f bar,TGAColor& color) override{
Vec2f uv=varying_uv*bar;
Vec3f n=(tri_normals*bar).normalize();
mat<3,3,float> A;
A[0]= proj<3,float>(tri_vertexes.get_col(1)-tri_vertexes.get_col(0));
A[1]=proj<3,float>(tri_vertexes.get_col(2)-tri_vertexes.get_col(0));
A[2]=n;
A=A.invert();
Vec3f bu(varying_uv[0][1]-varying_uv[0][0],varying_uv[0][2]-varying_uv[0][0],0);
Vec3f bv(varying_uv[1][1]-varying_uv[1][0],varying_uv[1][2]-varying_uv[1][0],0);
auto T=(A*bu).normalize();
auto B=(A*bv).normalize();
mat<3,3,float> cord;
cord.set_col(0,T);
cord.set_col(1,B);
cord.set_col(2,n);
auto read_n=model->normal(uv);
n=(cord*read_n).normalize();
float diff=std::max(0.f, n*light_dir);
Vec3f r= (n*(n*light_dir*2.f) - light_dir).normalize();
float spec=pow(std::max(0.f,r.z),model->specular(uv)+0.0001);
auto c=model->diffuse(uv);
auto p=tri_vertexes*bar;
auto s_p=shadowM* p;
s_p= s_p/s_p[3];
float shadow=1.0f;
int idx = int(s_p[0]) + int(s_p[1])*width;
if(idx>=0&&idx<width*height&&shadowBuffer[idx]>s_p[2]+0.01){
shadow-=0.8;
}
for(int i=0;i<3;i++){
color.raw[i]=std::min<float>(1.3*c.raw[i]*shadow*(diff+spec),255);
}
return true;
}
};

- 环境光
绘制环境光的方法是在一个半球面上均匀地采样点,对于每个光源点,用一张与纹理图大小相等的图来保存纹理图上点的是否可见的信息。最后把所有的图求平均。 这里要注意的是,在球面上均匀采样是指,单位面积采样点数量相同,但是球面上单位面元为 P A = p ( v ) d A = 1 4 π d A P_{A}=p(v) d A=\frac{1}{4 \pi} d A PA=p(v)dA=4π1dA 和theta角相关,所以如果直接对theta和phi角采样会得到错误采样。积分坐标变换后微元要乘以一个积分后坐标对积分前坐标的雅克比式,用来表示单位面积。
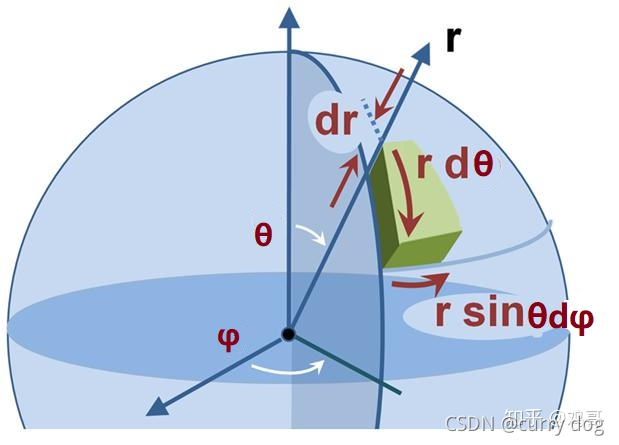 在球面上采样的正确方法
在球面上采样的正确方法
{ θ = arccos ( 1 − 2 ξ x ) ϕ = 2 π ξ y \left\{\begin{array}{l}\theta=\arccos \left(1-2 \xi_{x}\right) \\ \phi=2 \pi \xi_{y}\end{array}\right. { θ=arccos(1−2ξx)ϕ=2πξy
其中x,y都是0,1上均匀分布的变量
Geometry
Implicit
给出点之间的关系 f ( x , y , z ) = 0 f(x, y, z)=0 f(x,y,z)=0,并不给出实际的点。隐式的好处是方便判断一个点是否在表面内。
-
algebraic surface
就用不同的曲面方程来表示 -
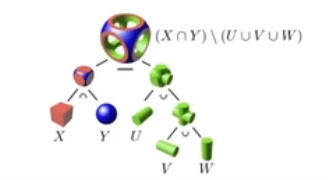
constructive solid geometry
通过一系列基本几何以及他们之间的布尔运算来定义几何。
-
signed distance function
空间中任何一个点的值定义为它到几何表面的距离,如果在表面外就是正数,如果在表面内就是负数。那既然已经可以用正负号来决定表面了为什么还需要距离呢,答案是方便进行插值,比如给定形状A和运动后的形状B,可以通过插值得到中间状态的形状。
TSDF
用于RGBD图的三维重建
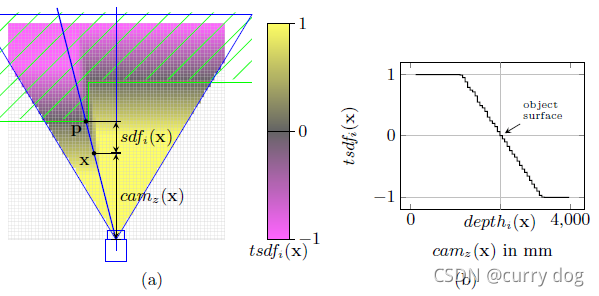
把场景分成n个体素,对于体素的每一个顶点x,按照当前相机位姿计算深度,并和它在图片中的投影点p的深度相减,就得到了x和表面的距离sdf(x),截断后变成了TSDF.
对多张图片计算tsdf并融合。 对于每一个体素,知道了8个顶点的tsdf值后,找到值为0的等值面作为最后输出的mesh。

-
level sets
ψ ( x , t ) \psi(\mathrm{x}, t) ψ(x,t)是一个函数,x是N维向量。 γ ( t ) \gamma(t) γ(t)是固定t,并且令 ψ ( x , t ) = 0 \psi(\mathrm{x}, t)=0 ψ(x,t)=0时得到的N-1维流型,也叫做level set。 考虑level set上的一个点x(t),有
ψ ( x ( t ) , t ) = C \psi(\mathbf{x}(t), t)=C ψ(x(t),t)=C
The particle speed ∂ x / ∂ t \partial \mathbf{x} / \partial t ∂x/∂t in the direction n \mathbf{n} n normal to γ ( t ) \gamma(t) γ(t) is given by the speed function F F F. Thus,
∂ x ∂ t ⋅ n = F \frac{\partial \mathbf{x}}{\partial t} \cdot \mathbf{n}=F ∂t∂x⋅n=F
where the normal vector n \mathbf{n} n is given by n = ∇ ψ / ∣ ∇ ψ ∣ . \mathbf{n}=\nabla \psi /|\nabla \psi| . n=∇ψ/∣∇ψ∣. By the chain rule we get,
ψ t + ∂ x ∂ t ⋅ ∇ ψ = 0 \psi_{t}+\frac{\partial \mathbf{x}}{\partial t} \cdot \nabla \psi=0 ψt+∂t∂x⋅∇ψ=0
and substitution yields
ψ t + F ∣ ∇ ψ ∣ = 0 \psi_{t}+F|\nabla \psi|=0 ψt+F∣∇ψ∣=0
上述构成一个hamilton jacobi equation,其中F是每一个点的变化速度,可以用曲率表示(用来平滑曲面),也可以通过学习得到。This equation can be solved using the stable, entropy-satisfying nite dierence schemes, borrowed from the literature on hyperbolic conservation laws
Explicit
所有的点都给出,或者通过 parameter mapping
比如uv空间中定义一些点,这些点可以通过函数映射到空间中。显示表示的好处是方便采样,但是判断一个点是否在表面内外就变得困难
-
point cloud
-
polygon mesh
-
subdivision, NURBS
bezier曲线的思想就是对初始集合中每一对前后点按照比例t进行线性插值,然后得到下一个集合,以此类推,直到最后只剩下唯一的点,得到的曲线是t的函数
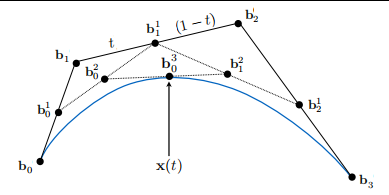
如果直接用公式来计算bezier曲线的话,那么如果有n+1个控制点就得到n阶多项式
b n ( t ) = ∑ j = 0 n b j B j n ( t ) \mathbf{b}^{n}(t)=\sum_{j=0}^{n} \mathbf{b}_{j} B_{j}^{n}(t) bn(t)=∑j=0nbjBjn(t)
其中 B i n ( t ) = ( n i ) t i ( 1 − t ) n − i B_{i}^{n}(t)=\left(\begin{array}{l} n \\ i \end{array}\right) t^{i}(1-t)^{n-i} Bin(t)=(ni)ti(1−t)n−i 可以看出多项式在t=0的值和b0相等,在t=1时的值和bn相等
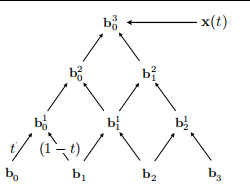
从上图可以看出,组合数C(2,3)等于于b2到达 b 0 3 b_{0}^{3} b03的路径数。bezier曲线还有一个性质是得到的曲线在控制点组成的凸包内,所以如果控制点在一条直线上,那么曲线也必须在同一条直线上。
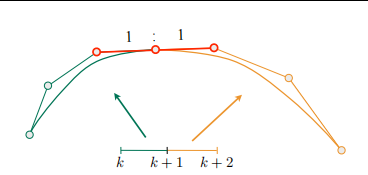
对于分段bezier,一般去四个控制点为一段,所以每一段是3次多项式,前一段的最后一个控制点等于下一段第0个控制点。可以证明b0和b1点的切线(方向和大小)为 b ′ ( 0 ) = 3 ( b 1 − b 0 ) ; b ′ ( 1 ) = 3 ( b 3 − b 2 ) \mathbf{b}^{\prime}(0)=3\left(\mathbf{b}_{1}-\mathbf{b}_{0}\right) ; \quad \mathbf{b}^{\prime}(1)=3\left(\mathbf{b}_{3}-\mathbf{b}_{2}\right) b′(0)=3(b1−b0);b′(1)=3(b3−b2), 所以如果想让段与段之间的交接点的切线连续的话必须满足 a n = b 0 = 1 2 ( a n − 1 + b 1 ) \mathbf{a}_{n}=\mathbf{b}_{0}=\frac{1}{2}\left(\mathbf{a}_{n-1}+\mathbf{b}_{1}\right) an=b0=21(an−1+b1)
对于曲面来说,一个曲面由4x4个控制点表示,首先在水平方向对t采样得到4条样条曲线,然后固定不同的t值,利用四条曲线上对应的四个点对v进行采样从而得到垂直方向的曲线。
B样条的改进之处是某个控制点的改变只会影响某一范围内的样条曲线。
曲面细分和简化
- 细分
loop subvision
以每个三角形边的中点作为新顶点,并且用周围老顶点的加权平均更新新节点的坐标,
对于老节点,用自身和邻居老节点更新更新坐标。
catmull-clark subvision
能应用于任何mesh,比如四边形mesh
在每一面的中点和1/2边处增加新顶点。
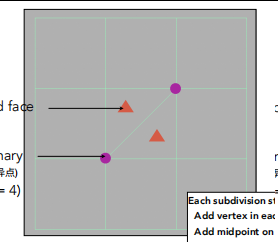
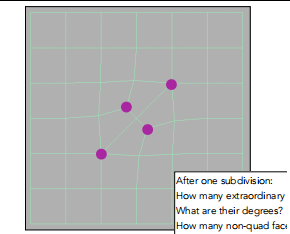
上图本来有两个三角形,但是经过一次迭代后变成了6个四边形。
- 简化
每次选择一条边,然后把这条边坍缩成一个点。
坍缩后点移动到离坍缩之前相关面最近的位置

USTC homework1
坑点
必须setMouseTracking(true); 才能在不按下鼠标的情况下追踪鼠标移动事件。