1. 微分算子法适用于求常系数线性非齐次微分方程的特解
(A)思想是将求导运算看成线性算符。右边非齐次项仍然是函数,就等价于求一个算符的逆的问题,同时在辅助特征值与特征函数理论,可以求解非齐次项是多项式,指数(三角函数通过欧拉公式化为指数)的形式。
(B)计算中通常结合位移定理以及级数,因式分解,短除法等方法使用。
(C)算子法的优点是能快速得到非齐次部分的特解而不需要特殊记忆特解的形式进行待定系数运算。这种方法能快速得到整个微分方程的通解。
注意: 算子法的题目比较简单无脑,所以近年来直接考通解的题目已经很少,逐渐变为在边界条件下求解的问题,这样算子法的优势就不如后面介绍的拉普拉斯变换方法。
2. 拉普拉斯变换适用于求解带初值条件的常系数线性非齐次微分方程
注意:常用的单边拉普拉斯变换求解的微分方程定义域只能在[0,+无穷)上
(A)拉普拉斯变换的思想是通过一个积分变换,将方程左右两边同时进行变换,使得微分方程变成一个代数方程,求解这个代数方程在做一个反变换,就能得到原方程的解。
(B)拉普拉斯变换的左边,形式与算子法很像,但会多出一个系数部分,为了完成非齐次项的拉普拉斯变换,需要记住常用函数的变换公式。最后还需要反变换回去。
(C)拉普拉斯变换法的优点在于能将题目所给的初值条件直接融入到等式中,而不需要最后再来待定系数。这种方法在某些问题上具有奇效。
例子:
2020考研数学真题
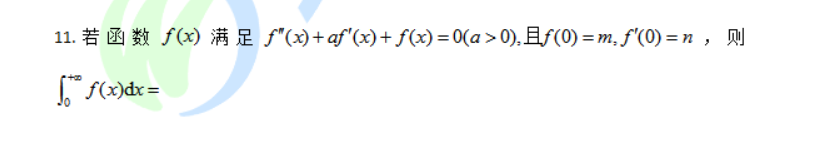
来看拉普拉斯变换的定义等式

显然,要计算的就是F(0)
根据拉普拉斯变化, s^2 F(s) - sn - m + a(sF(s) - m) + F(s) = 0
F(0) = m + am
2016考研数学真题
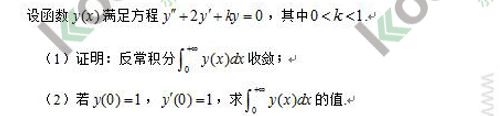
p^2 Y - p - 1 + 2(pY-1)+ kY = 0
令p=0, 答案就是Y(0) = 3/k
注意: 对这类问题拉普拉斯变换有奇效是因为巧妙的回避了反变换问题,仅在s域就解决了问题,如果要进行反变化,并不一定特别快速。但优点是反变换之后得到的就是原初值问题的解,而不需要在解线性方程确定系数。
3. 格林函数与卷积法
1. 格林函数方法的思想是非齐次项可以通过叠加原理分解为一连串的冲击响应,只要求解系统的冲击响应,那么整个响应可以通过冲击响应与输入函数卷积得到。格林函数方法可以直接给出方程的形式上的积分解。这点也可以从拉普拉斯变换看出来,两个拉普拉斯变化的乘积,返回到时域就是卷积。
2. 直接求解系统的冲击响应并不是一件容易的事,而且格林函数的定义其实严格说来也依赖于初值条件。所以这个问题可以又转化为拉普拉斯变换。
3. 可以这么理解,格林函数实际给出了方程的通解的形式,这种形式在特定问题下往往很有用。


(1) y = x -1, 这是可以直接观察出来或者用微分算子法快速求出来.
所以方程的通解是Ae(-x) +x-1
(2)构造一个方程的特解如下(空降)
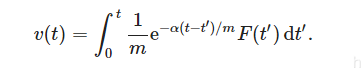
然后证明这是一个周期函数
注意:实际问题中格林函数的坑(因果性)





