傅里叶变换到拉普拉斯变换及收敛域分析

傅里叶变换得满足狄利赫里条件

狄利赫里条件为：
在这里插入图片描述

傅里叶变换有一个很大局限性，那就是信号必须满足狄利赫里条件才行，特别是那个绝对可积的条件，一下子就拦截掉了一大批函数。比如函数 f(t)=t^2 就无法进行傅里叶变换。这点难度当然拿不到聪明的数学家们，他们想到了一个绝佳的主意：把不满足绝对的可积的函数乘以一个快速衰减的函数，这样在趋于无穷时原函数也衰减到零了，从而满足绝对可积。换种说法，其就是一个信号 $x\left( t \right)$ 与 $e^{-\sigma t}$ 相乘后的傅里叶变换

拉普拉斯变换解决了不满足绝对可积条件的连续信号，变换到频率域的问题，同时也对“频率”的定义进行了扩充。
所以拉普拉斯变换与连续时间傅里叶变换的关系是：
拉普拉斯变换将频率从实数推广为复数，因而傅里叶变换变成了拉普拉斯变换的一个特例。
当s为纯虚数时，x(t)的拉普拉斯变换，即为x(t)的傅里叶变换。

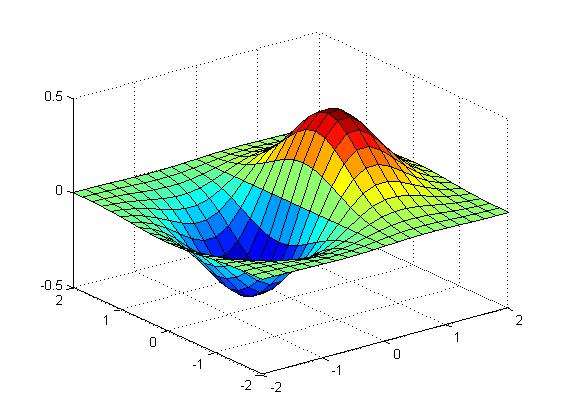
从幅度谱图像上看，拉普拉斯的函数是一个复平面函数，是一个面。是三维的

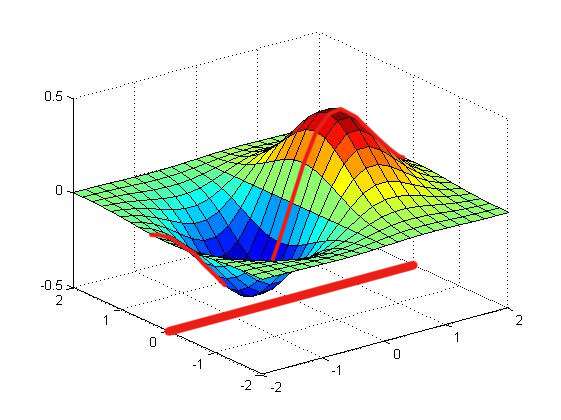
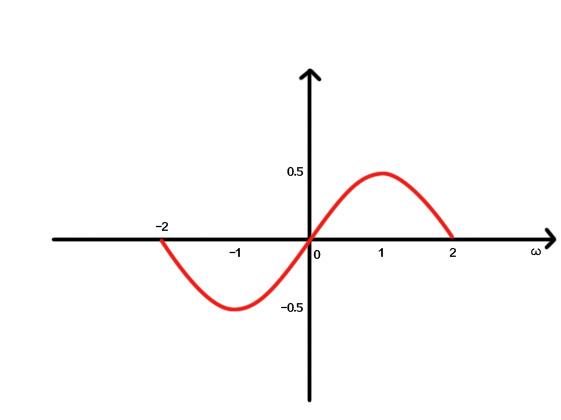
而傅里叶变换，是它的一个特例，就像这个平面中的一根线，即一个截面。是二维的

https://www.zhihu.com/question/22085329/answer/103926934

我们知道 $s=\sigma +jw$ ，s平面的横坐标便是复数s的实部 $\sigma$ ，纵坐标是虚部 $jw$ 。

注意上图，由无数条一竖竖直线组成，那其中的一竖直线代表什么意思呢？

我们先在其中取一竖固定的直线，此时 $\sigma$ 为一固定值，而 $jw$ 则从 $-\infty$ 到 $+\infty$ 变化。

$X\left( jw \right)= \int_{-\infty }^{+\infty } x\left( t \right) e^{-\sigma t} e^{jwt} dt$

当 $\sigma$ 为某一实数，信号 $x\left( t \right) e^{-\sigma t}$ 为一确定信号，从而也确定了 $X\left( jw \right)$ ，此时s平面中 $jw$ 与 $X\left( jw \right)$ 中的 $jw$ 是相对应的，即s平面中的一竖直线对应某一种确定信号的傅里叶变换！

再来总结一下s平面：横坐标 $\sigma$ 确定了某一信号，从而确定某一傅里叶变换。而纵坐标 $jw$ 与傅里叶变换 $X\left( jw \right)$ 的定义域jw相对应。

假设有一右边信号 $x\left( t \right)$ ，让该信号做拉普拉斯变换， $x\left( t \right)$ 先乘以 $e^{-\sigma t}$ 得到信号 $x\left( t \right) e^{-\sigma t}$ ，想一下，此时当 $\sigma <0$ 时，往右看， $e^{-\sigma t}$ 成增长趋势， $x\left( t \right) e^{-\sigma t}$ 并不是收敛函数。

因此，并不是所有的 $\sigma$ 都使 $x\left( t \right) e^{-\sigma t}$ 收敛。

所以，得出了收敛域的定义：在收敛域中，存在 $\forall \sigma$ ，使得 $x\left( t \right) e^{-\sigma t}$ 为收敛函数，从而 $X\left( jw \right)= \int_{-\infty }^{+\infty } x\left( t \right) e^{-\sigma t} e^{jwt} dt$ 。收敛。

下图 $x\left( t \right)$ 为一右边信号，使 $\sigma$ 等于某一实数 $\sigma_{o}$ ，使得 $x\left( t \right) e^{\sigma_{o} t}$ 为收敛函数，如图：

此时，当 $\sigma >\sigma _{o}$ 时， $e^{-\sigma t}$ 衰减速度更快，从而可知 $x\left( t \right) e^{-\sigma t}$ 也一定收敛。

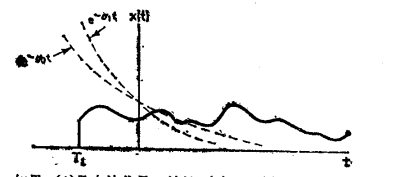
所以可以得到拉普拉斯收敛的一个性质

如果 $x\left( t \right)$ 是双边信号呢，我们可以把 $x\left( t \right)$ 分解成一左边信号 $x_{1} \left( t \right)$ 和右边信号 $x_{2} \left( t \right)$

$x\left( t \right)$ = $x_{1} \left( t \right)$ + $x_{2} \left( t \right)$ 。当 $x\left( t \right)$ 收敛时，也一定有 $x_{1} \left( t \right)$ 和 $x_{2} \left( t \right)$ 同时收敛，所以可知 $x\left( t \right)$ 的收敛域为 $x_{1} \left( t \right)$ 与 $x_{2} \left( t \right)$ 两者收敛域的重叠部分

傅里叶变换到拉普拉斯变换及收敛域分析

猜你喜欢