有关傅里叶变换、拉普拉斯变换、数字图像处理的卷积与卷积定理

本文用于学习中的记录，会在复习的过程中不断修订。

---

一.卷积

---

实值函数 $f_1(t)$和 $f_2(t)$在（ $-\infty,+\infty$）内有定义，积分 $\int_{-\infty}^{+\infty}f_1(τ)\, f_2(t-τ)dτ$为 $f_1(t)$与 $f_2(t)$的卷积

记作 $\bm{f_1(t)*f_2(t)=\int_{-\infty}^{+\infty}f_1(τ)\, f_2(t-τ)dτ}$

卷积满足交换律、结合律、分配率，实质就是在计算积分。

经典例题：
$f(t)=t^2u(t)$， $g(t)=\left\{\begin{aligned} 1,\qquad & |t|\leq1,\\0,\qquad&|t|>1. &\end{aligned}\right.$
求卷积：

函数图像：

当 $t<-1时$， $g(t)=0,f(t)*g(t)=0$
当 $-1<t<1时$， $f(t)*g(t)=\int_{-1}^{t}1*(t-τ)^2dτ=\frac{1}{3}(t+1)^3$
当t>1时，函数图像为：

虽然 $g(t)=0$，但积分值中依然包括 $f(t)*g(t)=\int_{-1}^{1}1*(t-τ)^2dτ=\frac{1}{3}(6t^2+2)$的部分。

故 $f(t)*g(t)=\left\{\begin{aligned}0,\,\,\,\quad\quad\qquad&t<-1\\ \frac{1}{3}(t+1)^3,\quad&-1<t<1\\\frac{1}{3}(6t^2+2),&\quad t>1\end{aligned}\right.$

---

二.卷积定理

---

由卷积与傅里叶变换得：

$\mathscr{F}[f_1(t)*f_2(t)]=\int_{-\infty}^{+\infty}f_1(t)*f_2(t)\,e^{-jwt}dt=F_1(w)·F_2(w)$

由卷积与拉普拉斯变换得：

$\mathscr{L}[f_1(t)*f_2(t)]=\int_{0}^{+\infty}f_1(t)*f_2(t)\,e^{-st}dt=F_1(w)·F_2(w)$

化简下来实际是在求二重积分

想更直观地了解拉氏变换可参考这篇：拉普拉斯变换【直观解释】—复变函数与积分变换学习笔记

---

三.卷积在数字图像处理中的应用

---

信号有很多种类，有连续的，离散的，一维的，多维的，图像就属于二维信号，可以分割成很多的像素点，并有RGB三原色通道。

只要稍稍接触点计算机视觉、图像处理的，就肯定离不开卷积。

在最开始的定义式 $\bm {h(x,y)=f_1(x,y)*f_2(x,y)=\int_{-\infty}^{+\infty}f_1(x,y)\, f_2(x-τ,y-τ)dτ}$ 中

如果 $f_1(x,y)$和 $h(x,y)$表示图像，则卷积 就变成了对像素点的加权计算，冲激响应 $f_2(x,y)$就可以看成是一个卷积模板。对图像中每一个像素点[x,y]输出响应 值h(x,y)是通过平移卷积模板到像素点[x,y] 处,计算模板与像素点[x,y]邻域加权得到的 ，其中各加权值就是卷积模板中的对应值 。 在图像处理中的卷积 都是针对某像素的邻域进行的，它实现了一种邻域运算 ，即某个像素点 的结果不 仅仅与本像素点灰度有 关，而且与其邻域点的值有关。其实质就是对图像邻域像素的加权 求和得到输出像素值，其中的权矩阵称为卷积核(所有卷积核的行、列数都是奇数 )，也就是图像滤波器 。

图中中间那个3*3矩阵就是卷积核（或叫做计算模板），即式中的 $f_2(x,y)$，通过与input中的原始二维数组进行计算，计算过程如动图所示

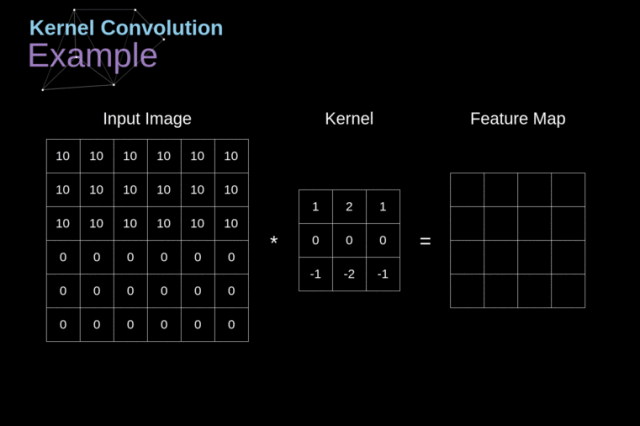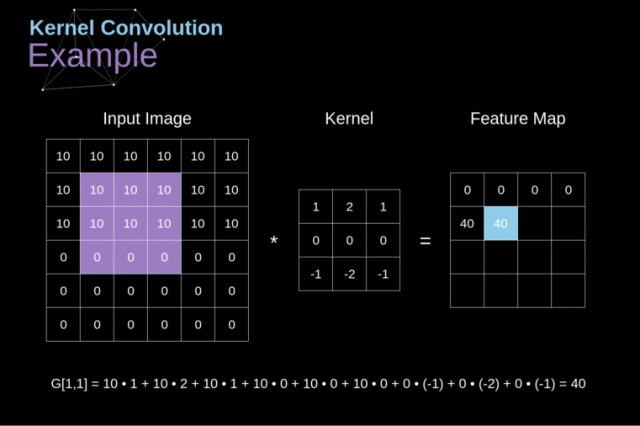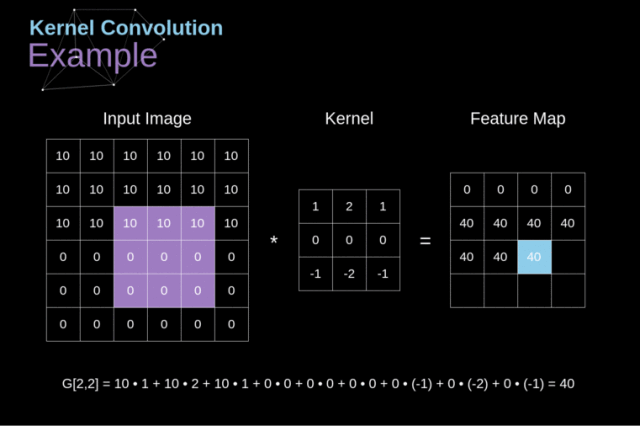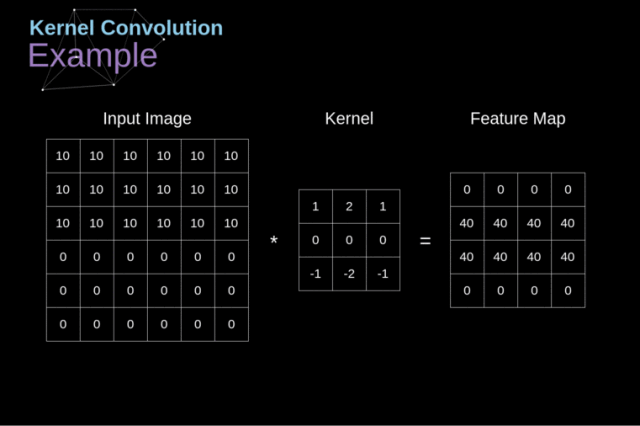
就得到了卷积的结果。

选取不同的卷积核，会有不同的滤波效果，比如高通低通，对应滤波出来的效果就是锐化和平滑。

在Python Opencv中

def zi_image(src):
    kernel1 = np.array([[1, 0, -1], [1, 0, -1], [1, 0, -1]], np.float32)
    src = cv.filter2D(src, -1, kernel1)
    cv.imshow("sharpening", src)
    cv.imwrite('filter.jpg', src, [int(cv.IMWRITE_JPEG_QUALITY), 100])

卷积可由cv.filter2D函数来实现，不同的卷积核得到的效果自然不同。

下面随便卷两个试试：