02. 改善深层神经网络 —— week1 超参数调试、正则化以及优化

内容涉及超参数调优，如何构建数据，以及如何确保优化算法快速运行，从而使学习算法在合理的时间内完成自我学习。

1.1 训练、验证、测试集

应用型机器学习是一个高度迭代的过程。创建高质量的训练集，验证集和测试集可以提高迭代的速度。我们通常将训练数据划分为三部分：

• 训练集：用训练集对算法或模型进行训练过程。
• （交叉）验证集：交叉验证，选择模型。
• 测试集：选定模型后，在测试集进行评估，获得模型运行的无偏估计。

数据划分

小数据时代

在小数据量的时代，如：100、1000、10000的数据量大小，可以将data做以下划分：

• 无验证集的情况：70% / 30%；
• 有验证集的情况：60% / 20% / 20%；

通常在小数据量时代，以上比例的划分是非常合理的。

大数据时代

大数据时代，数据量如百万级别，验证集和测试集占数据总量的比例会趋向于变得更小。

验证集的目的是为了验证不同的算法哪种更加有效，所以验证集只要足够大能够验证大约2-10种算法哪种更好就足够了，不需要使用20%的数据作为验证集。如百万数据中抽取1万的数据作为验证集就可以了。

测试集的主要目的是评估模型的效果，如在单个分类器中，往往在百万级别的数据中，我们选择其中10000条数据足以评估单个模型的效果。

• 100万数据量：98% / 1% / 1%；
• 超百万数据量：99.5% / 0.25% / 0.25%（或者99.5% / 0.4% / 0.1%）

Note.
建议验证集和测试集来自于同一个分布，这样可以使得机器学习算法变得更快；
如果不需要用无偏估计来评估模型的性能，则可以不需要测试集。

1.2 偏差、方差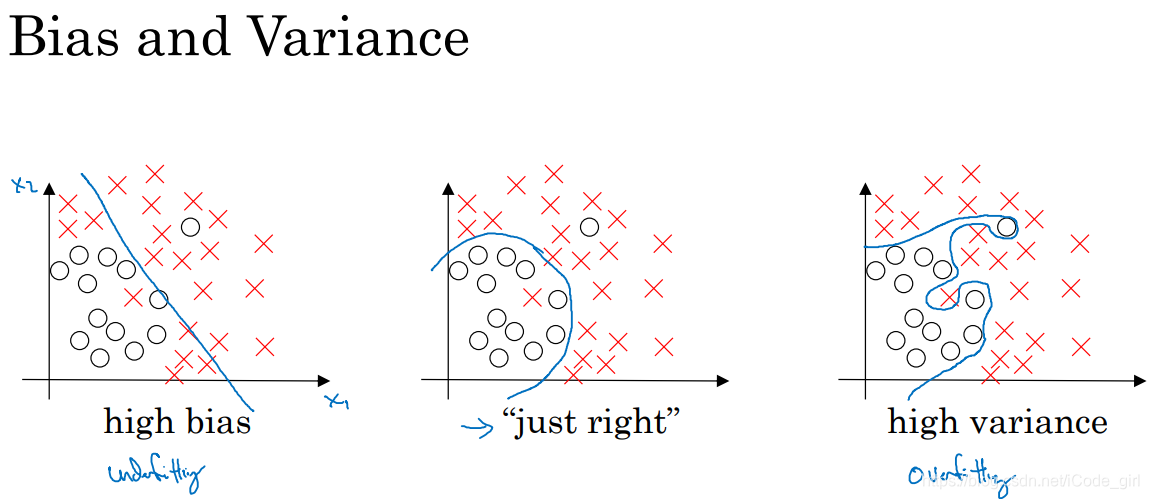

如图为只有两个特征的二维数据集三种拟合情况。欠拟合（高偏差），适度拟合，过拟合（高方差）。

多维数据集中，绘制数据和可视化分割边界无法实现，此时分析偏差和方差的关键数据为训练集误差和验证集误差。

例如：

验证集误差高对应高方差，训练集误差高对应高偏差。

最优误差通常也称为贝叶斯误差。

分类器高偏差和高方差时举例：

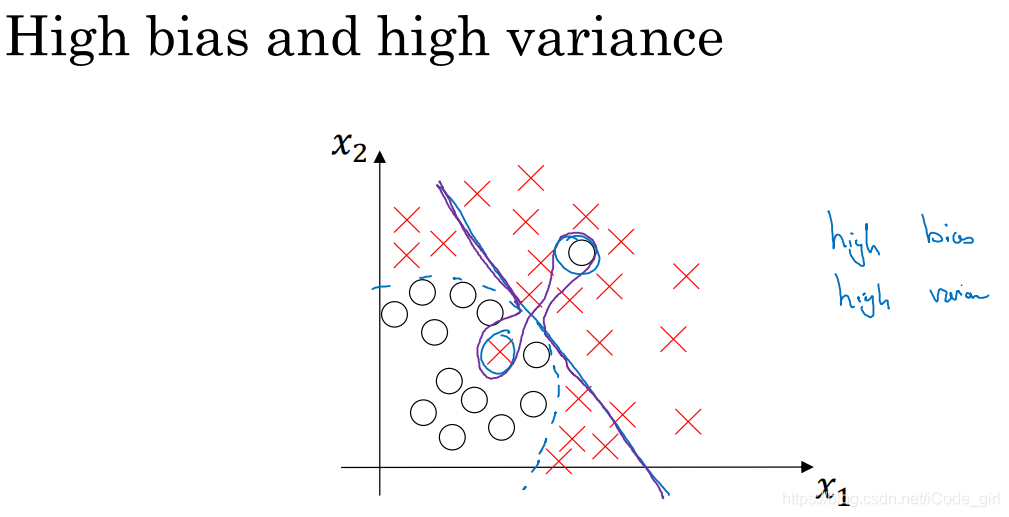
偏差高是因为它几乎是一条线性分类器，并未拟合数据，蓝色的二次曲线能够很好地拟合数据，曲线中间部分灵活性非常高，过度拟合了两个错误样本，有些数据区域偏差高，有些数据区域方差高。二维数据集这种分类函数很奇怪，高维数据集时出现可能性高一点。

1.3 机器学习基础

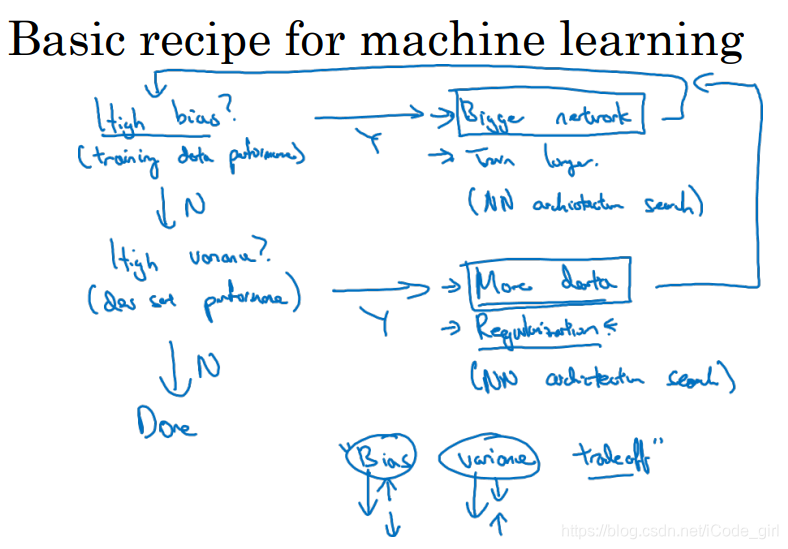
初始模型训练完成后，首先估计算法的偏差，如果偏差很高，甚至无法拟合数据集，那么重新选择一个新网络，比如含有更多隐层或者隐藏单元的网络，或者花费更多时间训练算法，或者尝试更先进的优化算法。不断尝试上述方法，直到解决偏差问题，可以拟合数据。然后通过验证集估计算法的方差，如果方差高，最好的解决办法时采用更多的数据，也可以通过正则化减少过拟合。如果能找到更合适的神经网络框架，可以同时减少方差和偏差。
不断尝试以上，直到找到一个低偏差、低方差的框架，done。

在当前的深度学习和大数据时代，只要持续训练一个更大的网络结构，准备更多数据，正则适度，通常可以在不过多影响偏差的同时减少方差。这是深度学习对监督式学习大有裨益的一个重要原因，也是我们不用太过关注如何平衡偏差和方差的一个重要原因。

1.4 正则化

解决过拟合（高方差）可以通过正则化或者获取更多数据来解决。
利用正则化来解决High variance 的问题，正则化是在 Cost function 中加入一项正则化项，惩罚模型的复杂度。

Logistic regression

加入正则化项的代价函数：

$J(w,b)=\dfrac{1}{m}\sum\limits_{i=1}^{m}l(\hat y^{(i)},y^{(i)})+\dfrac{\lambda}{2m}||w||_{2}^{2}$

上式为逻辑回归的L2正则化。

L2正则化： $\dfrac{\lambda}{2m}||w||_{2}^{2} = \dfrac{\lambda}{2m}\sum\limits_{j=1}^{n_{x}} w_{j}^{2}=\dfrac{\lambda}{2m}w^{T}w$

L1正则化： $\dfrac{\lambda}{2m}||w||_{1}=\dfrac{\lambda}{2m}\sum\limits_{j=1}^{n_{x}}|w_{j}|$

其中 $\lambda$ 为正则化因子。

L1正则化会使模型变得稀疏，却没有降低太多存储内存。训练网络时，越来越倾向于使用 L2 正则化。

注意：lambda 在python中属于保留字，所以在编程的时候，用“lambd”代表这里的正则化因子 $\lambda$ 。

Neural network

加入正则化项的代价函数：

$J(w^{[1]},b^{[1]},\cdots,w^{[L]},b^{[L]})=\dfrac{1}{m}\sum\limits_{i=1}^{m}l(\hat y^{(i)},y^{(i)})+\dfrac{\lambda}{2m}\sum\limits_{l=1}^{L}||w^{[l]}||_{F}^{2}$

其中 $||w^{[l]}||_{F}^{2}=\sum\limits_{i=1}^{n^{[l-1]}}\sum\limits_{j=1}^{n^{[l]}}(w_{ij}^{[l]})^{2}$，因为 w 的大小为 $(n^{[l-1]},n^{[l]})$ ，该矩阵范数被称为“Frobenius norm”

Weight decay

在加入正则化项后，梯度变为：

$dW^{[l]} = (form\_backprop)+\dfrac{\lambda}{m}W^{[l]}$

则梯度更新公式变为：

$W^{[l]}:= W^{[l]}-\alpha dW^{[l]}$

代入可得：

$W^{[l]}:= W^{[l]}-\alpha [ (form\_backprop)+\dfrac{\lambda}{m}W^{[l]}]\\ = W^{[l]}-\alpha\dfrac{\lambda}{m}W^{[l]} -\alpha(form\_backprop)\\=(1-\dfrac{\alpha\lambda}{m})W^{[l]}-\alpha(form\_backprop)$

其中， $(1-\dfrac{\alpha\lambda}{m})$ 为一个 <1 的项，会给原来的 $W^{[l]}$一个衰减的参数，所以L2范数正则化也被称为“权重衰减（Weight decay）”。

1.5 为什么正则化可以减少过拟合

$J(w^{[1]},b^{[1]},\cdots,w^{[L]},b^{[L]})=\dfrac{1}{m}\sum\limits_{i=1}^{m}l(\hat y^{(i)},y^{(i)})+\dfrac{\lambda}{2m}\sum\limits_{l=1}^{L}||w^{[l]}||_{F}^{2}$

正则项可以避免数据权值矩阵过大， $\lambda$增大时， $w$会减小，可以消除或减少许多隐藏单元的影响，简化网络，过拟合更不容易发生。

假设下图的神经网络结构属于过拟合状态：

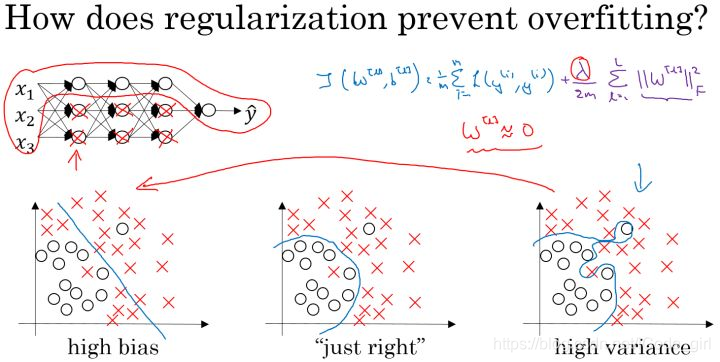
对于神经网络的 Cost function：

$J(w^{[1]},b^{[1]},\cdots,w^{[L]},b^{[L]})=\dfrac{1}{m}\sum\limits_{i=1}^{m}l(\hat y^{(i)},y^{(i)})+\dfrac{\lambda}{2m}\sum\limits_{l=1}^{L}||w^{[l]}||_{F}^{2}$

加入正则化项，直观上理解，正则化因子 \lambda 设置的足够大的情况下，为了使代价函数最小化，权重矩阵 W 就会被设置为接近于0的值。则相当于消除了很多神经元的影响，那么图中的大的神经网络就会变成一个较小的网络。

当然上面这种解释是一种直观上的理解，但是实际上隐藏层的神经元依然存在，但是他们的影响变小了，便不会导致过拟合。

数学解释：

假设神经元中使用的激活函数为 g(z)=\tanh(z) ，在加入正则化项后：

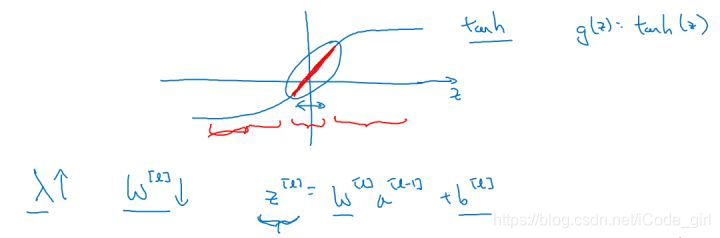
当 $\lambda$ 增大，导致 $W^{[l]}$ 减小， $Z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$ 便会减小，由上图可知，在 $z$ 较小的区域里， $\tanh(z)$ 函数近似线性，所以每层的函数就近似线性函数，整个网络就成为一个简单的近似线性的网络，从而不会发生过拟合。

1.6 Dropout 正则化

Dropout（随机失活）就是在神经网络的Dropout层，为每个神经元结点设置一个随机消除的概率，保留下来的神经元组成一个节点较少，规模较小的网络，进行训练。

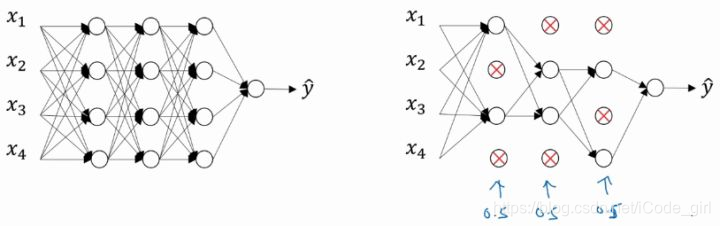
实现Dropout的方法：反向随机失活（Inverted dropout）

首先假设对 layer 3 进行dropout：

keep_prob = 0.8  # 设置神经元保留概率
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob
a3 = np.multiply(a3, d3)
a3 /= keep_prob

这里解释下为什么要有最后一步：a3 /= keep_prob

依照例子中的 keep_prob = 0.8 ，那么有大约20%的神经元被删除，也就是说 $a^{[3]}$ 中有20%的元素被归零，在下一层的计算中 $Z^{[4]}=W^{[4]}\cdot a^{[3]}+b^{[4]}$ ，为了不影响 $Z^{[4]}$ 的期望值，需要 $W^{[4]}\cdot a^{[3]}$的部分除以一个keep_prob。

Inverted dropout 通过对“a3 /= keep_prob”,则保证无论 keep_prob 设置为多少，都不会对 $Z^{[4]}$ 的期望值产生影响。

Notation： 在测试阶段不要用dropout，因为那样会使得预测结果变得随机。

对于每个样本，梯度下降的每次循环，要删除的节点集合都是重新随机的么。这里有点疑惑。

1.7 dropout 理解

以单个神经元为例，单个神经元的工作就是接收输入，并产生一些有意义的输出，加入了Dropout以后，输入的特征都是有可能会被随机清除的，所以该神经元不会再特别依赖于任何一个输入特征，也就是说不会给任何一个输入设置太大的权重。所以通过传播过程，dropout将产生和L2范数相同的收缩权重的效果。

对于不同的层，设置的keep_prob也不同，一般来说神经元较少的层，会设 keep_prob = 1.0，神经元多的层，则会将keep_prob设置的较小。

Dropout 缺点：

dropout的一大缺点就是其使得 Cost function不能再被明确的定义，以为每次迭代都会随机消除一些神经元结点，所以我们无法绘制出每次迭代 J(W,b) 下降的图，如下：

使用Dropout：

• 关闭dropout功能，即设置 keep_prob = 1.0；
• 运行代码，确保 J(W，b) 函数单调递减；
• 再打开 dropout 。

1.8 其它正则化方法

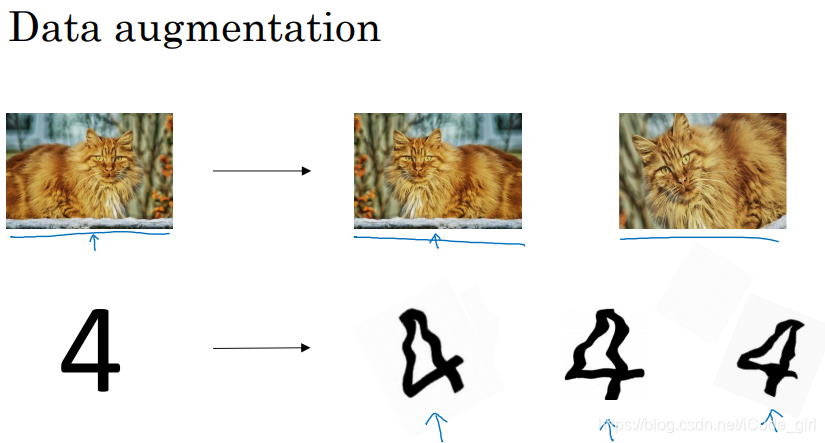
Data augmentation：

获取更多训练数据代价太高时，可以对已有样本做一些处理，得到一些假数据，扩增算法数据，进而正则化数据集。

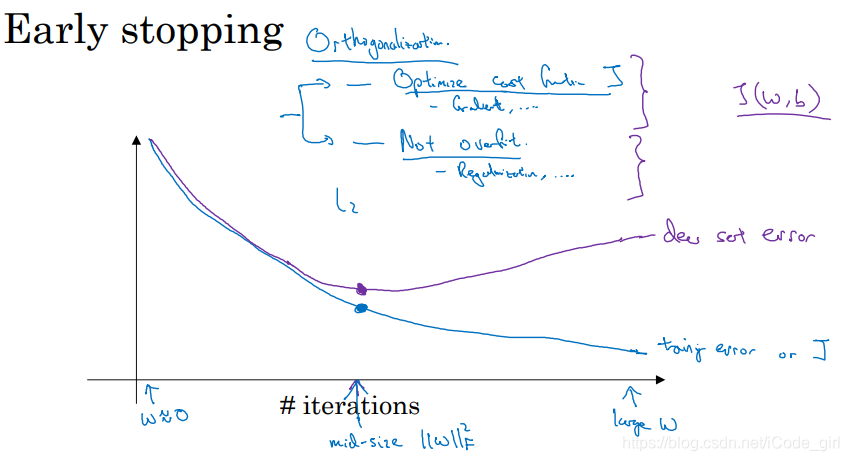
Early stopping：

运行梯度下降时，绘制代价函数J的优化过程，在交叉验证集的误差上升之前的点停止迭代，避免过拟合。

这种方法的缺点是无法同时解决bias和variance之间的最优。

优点是只运行一次梯度下降，就可以找出 $w$的较小值，中间值和较大值。

1.9 正则化输入

• 归一化输入可以提高训练神经网络的速度。
• 归一化输入两个步骤：零均值化和归一化方差。

下图为对二维数据集做归一化的过程，最后数据集两个维度的方差都等于1。

Note：
训练集和测试集应该用相同的 $\mu$和 $\sigma^2$进行归一化，其中 $\mu$和 $\sigma^2$是由训练集计算得来的。

为什么对数据集归一化

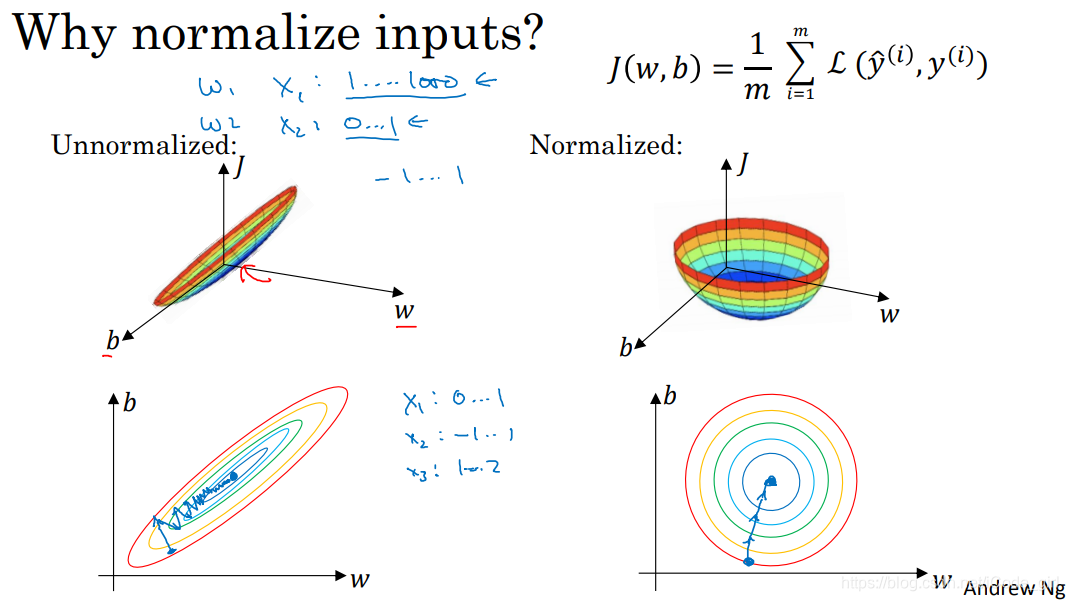
如果使用非归一化特征，代价函数就会如左上图，非常细长狭窄，运行梯度下降时必须使用一个非常小的学习率，因为根据起始位置可能需要多次迭代过程才能找到最小值。对数据进行归一化，代价函数会更加对称，运行梯度下降算法时，无论从哪个位置开始，都能更直接的找到最小值，可以使用较大步长。特征在相似范围内，代价函数更容易优化。

1.10 梯度消失与梯度爆炸

在梯度函数上出现的以指数级递增或者递减的情况就分别称为梯度爆炸或者梯度消失。

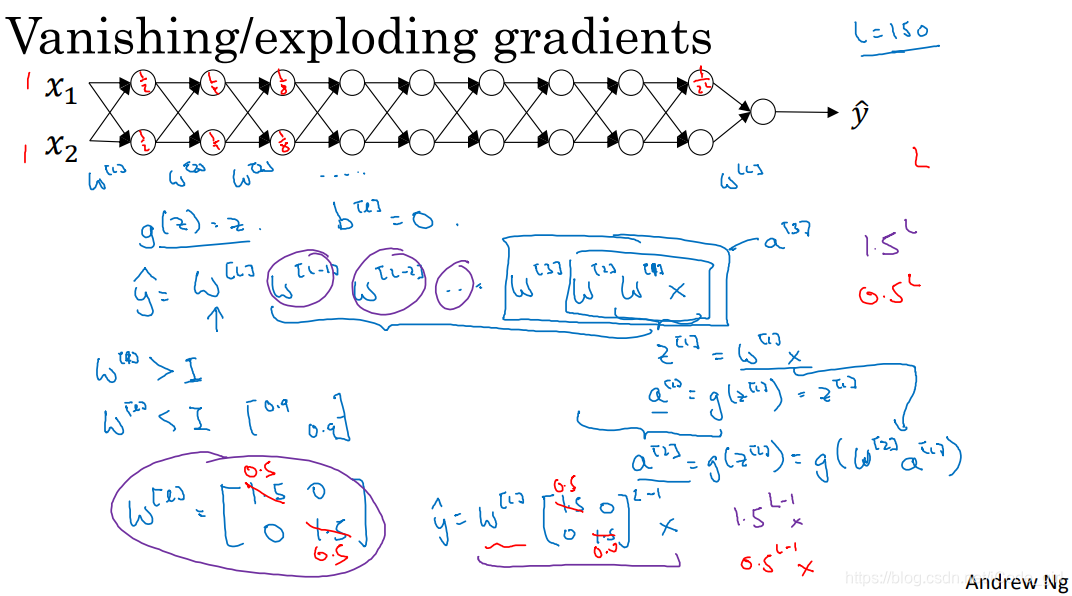
假设激活函数 $g(z)=z$（线性激活函数）， $b^{[l]}=0$，则 $\hat{y}=w^{[L]}*w^{[L-1]}*w^{[L-2]}......*w^{[3]}*w^{[2]}*w^{[1]}*x$，假设 $w^{[l]}$相等，忽略 $w^{[L]}$维度区别，则 $\hat{y}={w^{[l]}}^{(l-1)}*x$。训练深度神经网络时，L值比较大，如果 $w$值比1大，最后呈会指数爆炸增长，比1小会呈指数减小。

上面的情况对于导数也是同样的道理，所以在计算梯度时，根据情况的不同，梯度函数会以指数级递增或者递减，导致训练导数难度上升，梯度下降算法的步长会变得非常非常小，需要训练的时间将会非常长。

1.11 神经网络的权重初始化

以单个神经元举例：

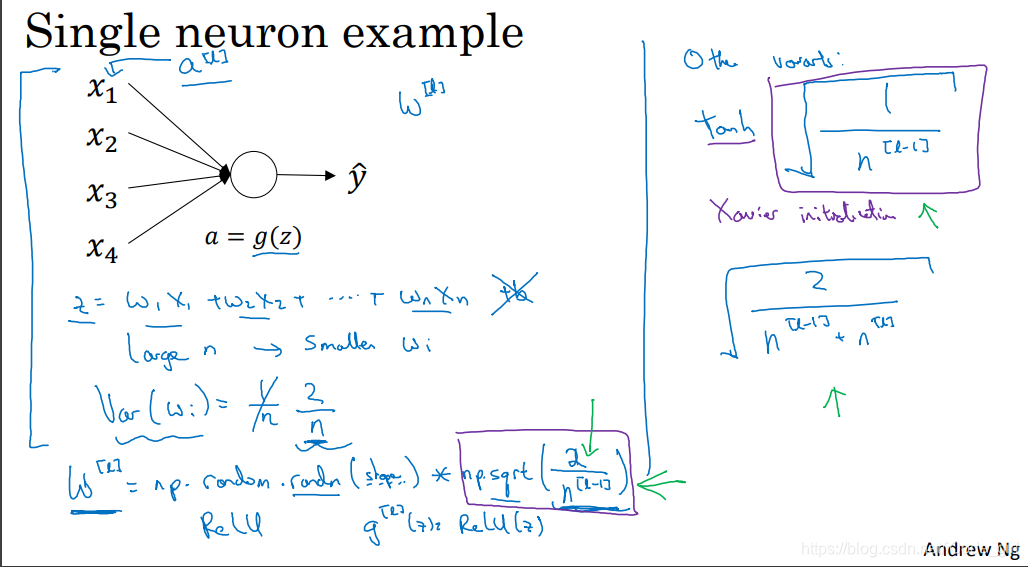
为了预防 $z$值过大或过小， $n$越大，我们希望 $w^{[i]}$越小。其中一种初始化方法就是使 $w^{[i]}=1/n$，（ $n$表示神经元的输入特征数量）。

W[l] = np.random.randn(W[l].shape[0],W[l].shape[1])* np.sqrt(1/n[l-1])

这么做是因为，如果激活函数的输入 x 近似设置成均值为0，标准方差1的情况，输出 z 也会调整到相似的范围内。虽然没有解决梯度消失和爆炸的问题，但其在一定程度上确实减缓了梯度消失和爆炸的速度。

不同激活函数的 Xavier initialization：

• 激活函数使用Relu： $Var(w_{i})=\dfrac{2}{n}$；
• 激活函数使用tanh： $Var(w_{i})=\dfrac{1}{n}$；
• 其中n是输入的神经元个数，也就是 $n^{[l-1]}$ 。

1.12 梯度的数值逼近

执行梯度检验时我们使用双边误差，而不使用单边误差，因为它不够准确。
使用双边误差判断函数 $g(\theta)$是否正确实现了函数 $f$的偏导。

1.13 梯度检验

检验backprop的实施是否正确。

连接参数：

因为我们的神经网络中含有大量的参数： $W^{[1]},b^{[1]},\cdots,W^{[L]},b^{[L]}$ ，为了做梯度检验，需要将这些参数全部连接起来，reshape成一个大的向量 $\theta$ 。

同时对 $dW^{[1]},db^{[1]},\cdots,dW^{[L]},db^{[L]}$执行同样的操作：

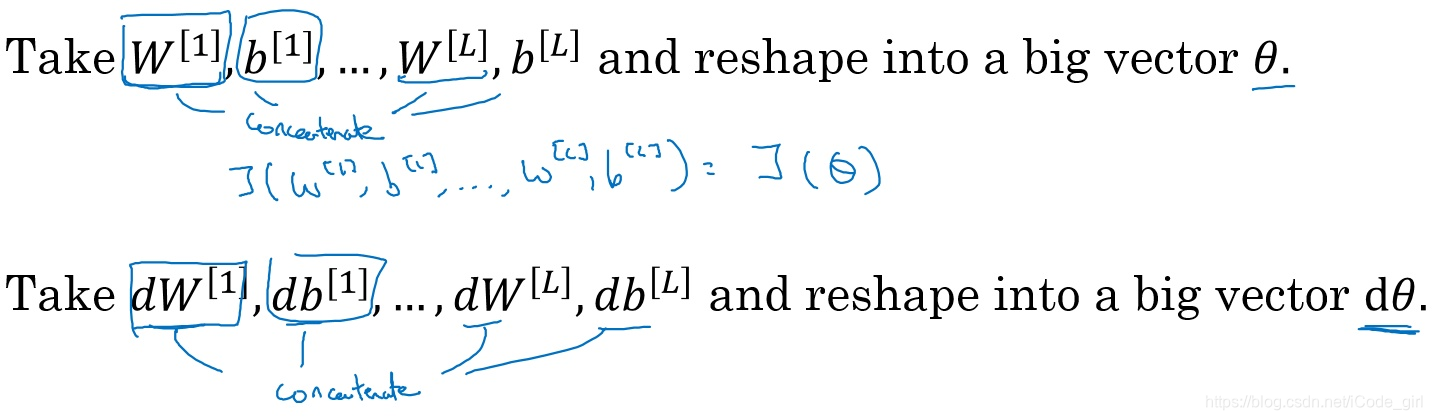
进行梯度检验：

进行如下图的梯度检验：

对每个 $\theta$组成元素，使用双边误差计算 $d\theta_{approx}$。

判断 $d\theta_{approx}\approx d\theta$ 是否接近。

判断公式：

$\dfrac {||d\theta_{approx}-d\theta||_{2}}{||d\theta_{approx}||_{2}+||d\theta||_{2}}$

其中， $“ ||\cdot ||_{2} ”$表示欧几里得范数，它是误差平方之和，然后求平方根，得到的欧氏距离。

1.14 实现梯度检验的Notes

• 不要在训练中使用梯度检验，它只用于调试，使用完毕关闭dbug的功能。
• 如果算法的梯度检验失败，要检查所有项，找出错误，也就是说要找出哪个 $d\theta_{approx}[i]$与 $d\theta[i]$的值相差比较大；
• 实施梯度检验时，如果使用正则化，注意要包括正则项。
• 梯度检验不能与dropout同时使用。因为每次迭代过程中，dropout会随机消除隐层单元的不同子集，难以计算dropout在梯度下降上的代价函数J。
• 在随机初始化过程中运行梯度检验，然后训练网络，w和b会有一段时间远离0，反复训练网络后，重新运行梯度检验。

参考资料

[1] 笔记连载 https://blog.csdn.net/koala_tree/article/details/78125697
[2] 吴恩达网易云深度学习课程

以上内容全部来自参考资料。
有些地方其实没太理解，在编程作业里好好体会吧。