02. 改善深层神经网络 —— week1 超参数调试、正则化以及优化（编程作业）

1 初始化参数

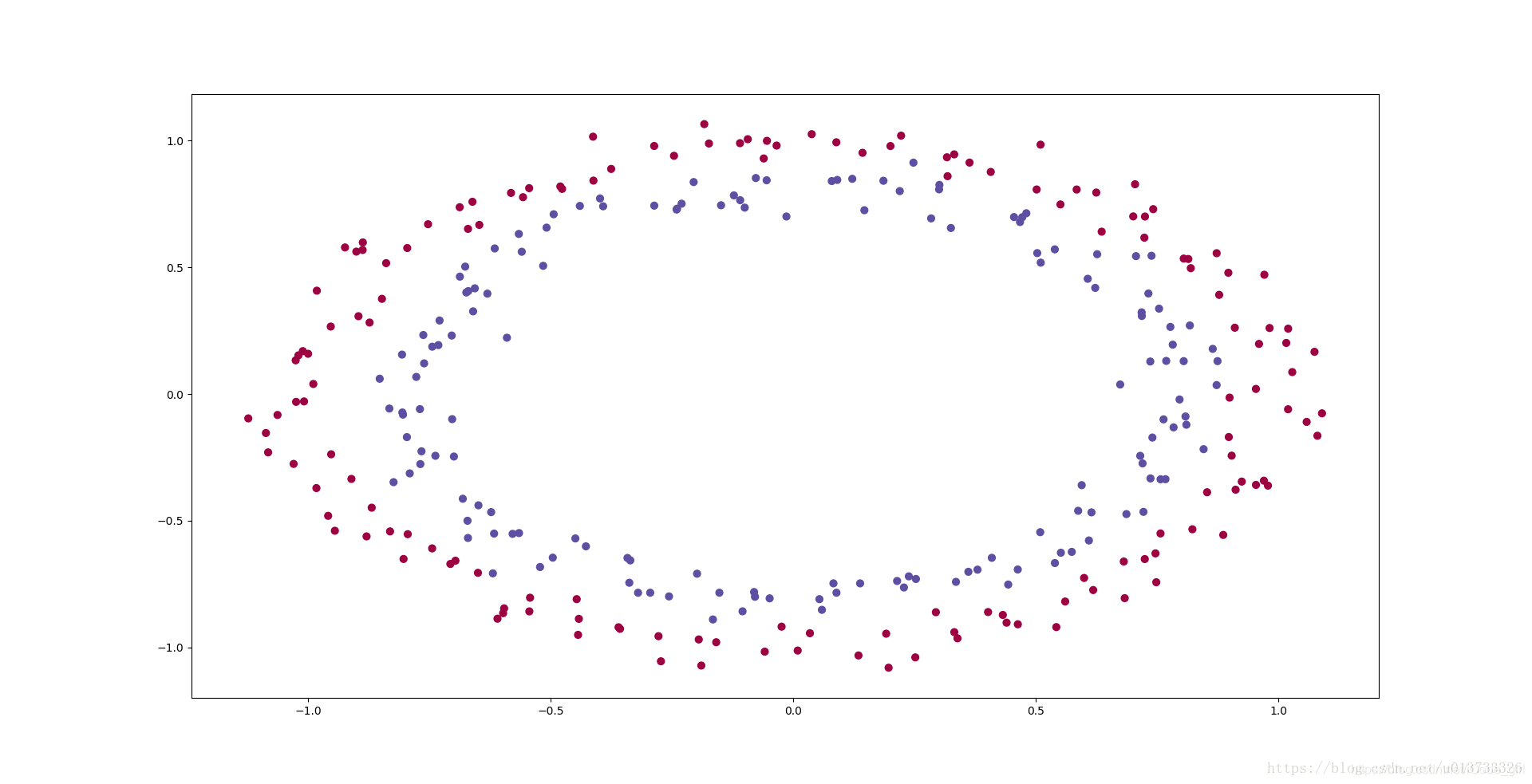
尝试了三种初始化方法，比较分类和代价函数变化。

全部初始化为0

parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l - 1]))

算法性能差，运行过程中成本没有真正降低。


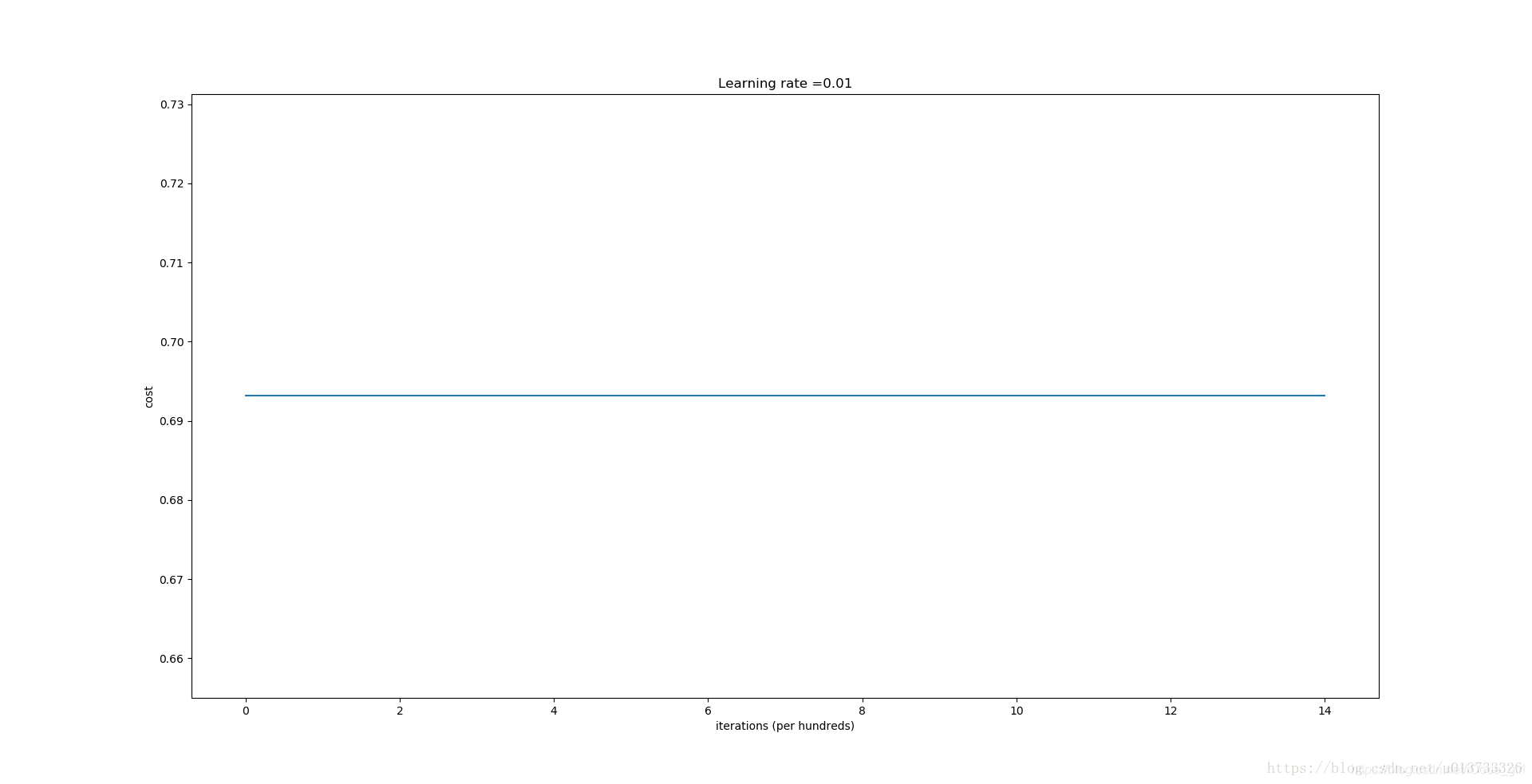
分类失败，该模型预测每个都为0。通常来说，零初始化都会导致神经网络无法打破对称性，最终导致的结果就是无论网络有多少层，最终只能得到和Logistic函数相同的效果。

w初始化为大的随机值，b为0

parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * 10

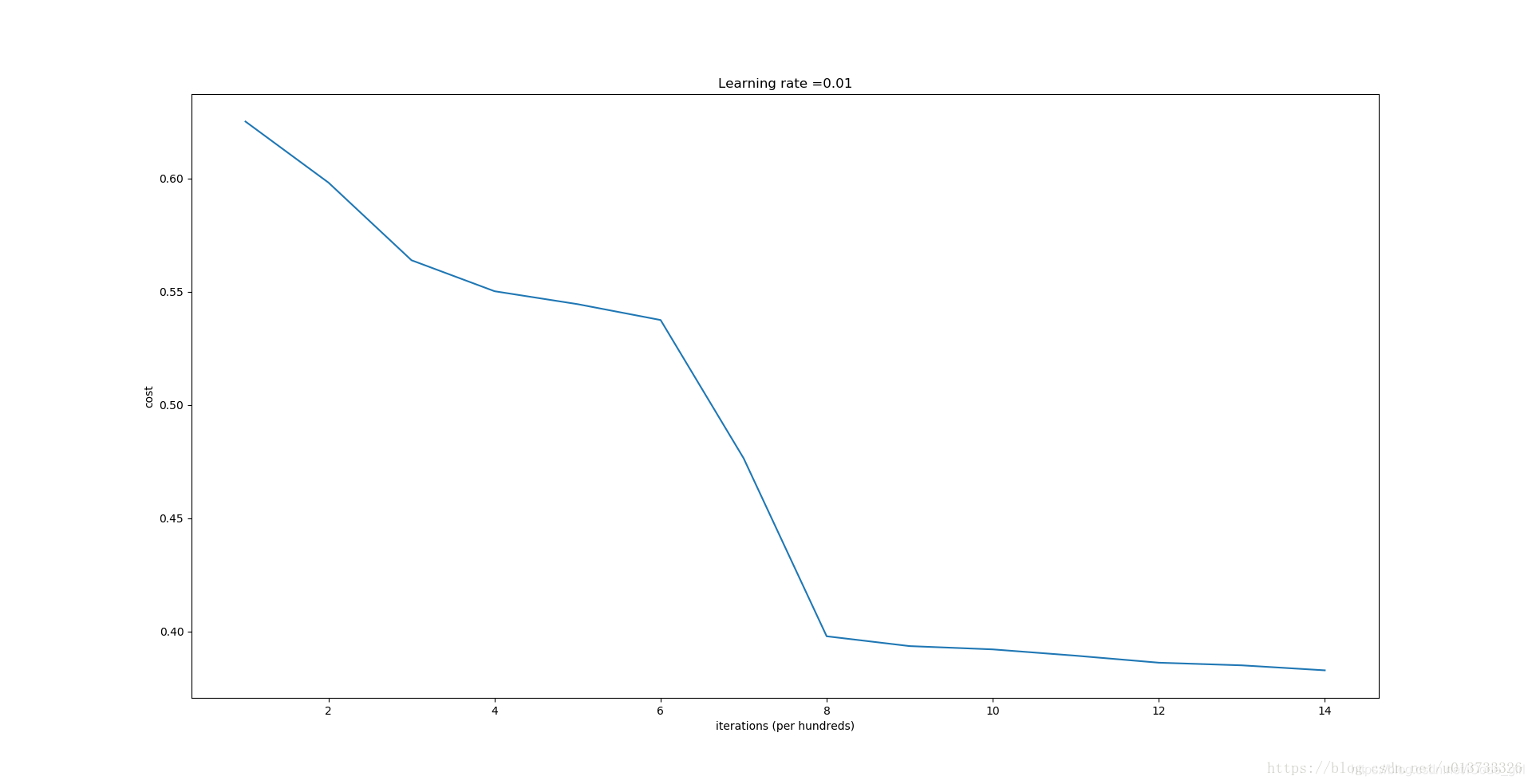
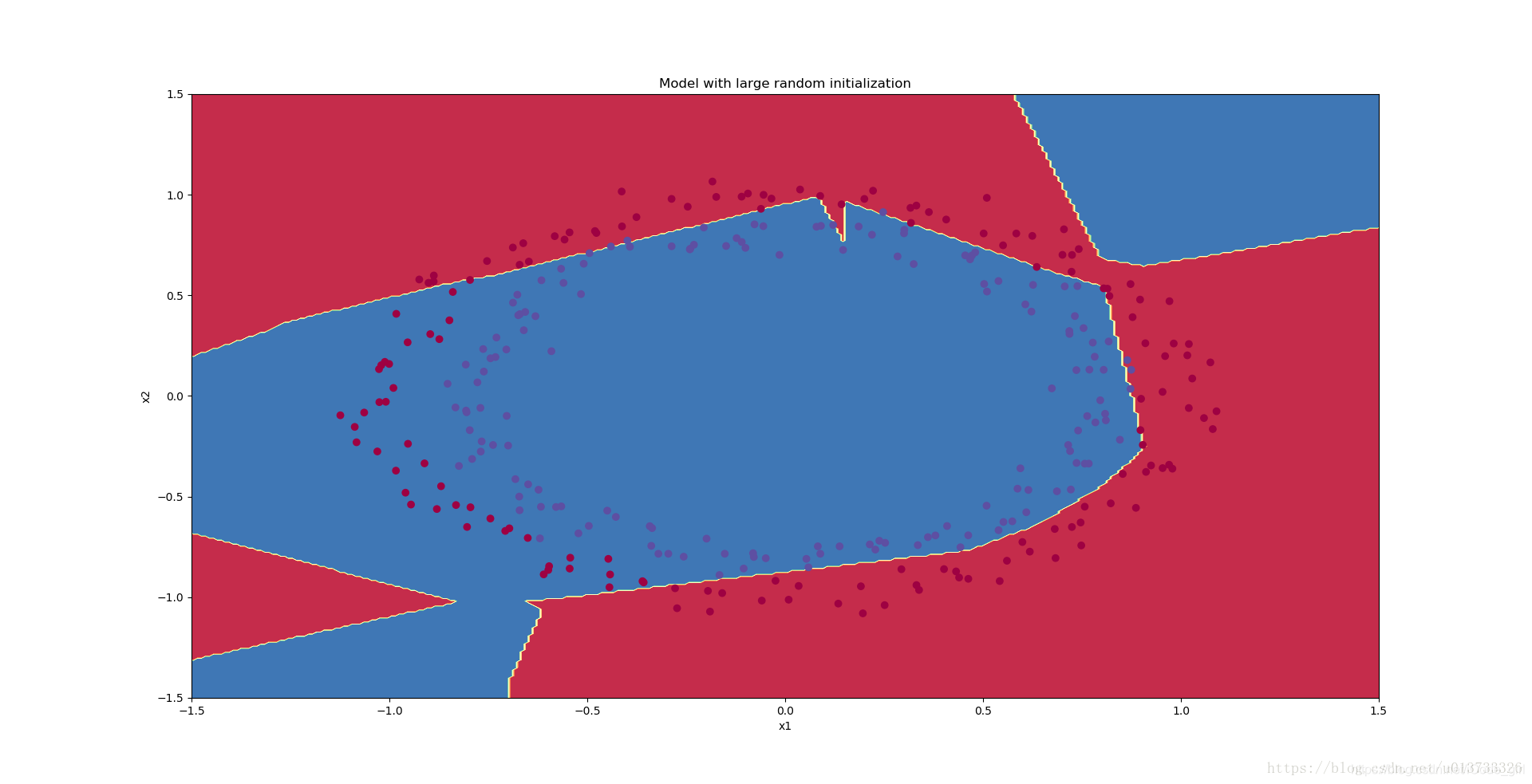
误差开始很高，这是因为由于具有较大的随机权重，最后一个激活(sigmoid)输出的结果非常接近于0或1，而当它出现错误时，它会导致非常高的损失。如果没有很好地初始化参数，会导致梯度消失、爆炸，也会减慢优化算法。如果我们对这个网络进行更长时间的训练，我们将看到更好的结果，但是使用过大的随机数初始化会减慢优化的速度。

使用公式 $\sqrt{\frac{2}{上一层的维度}}$抑制

parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2 / layers_dims[l - 1])

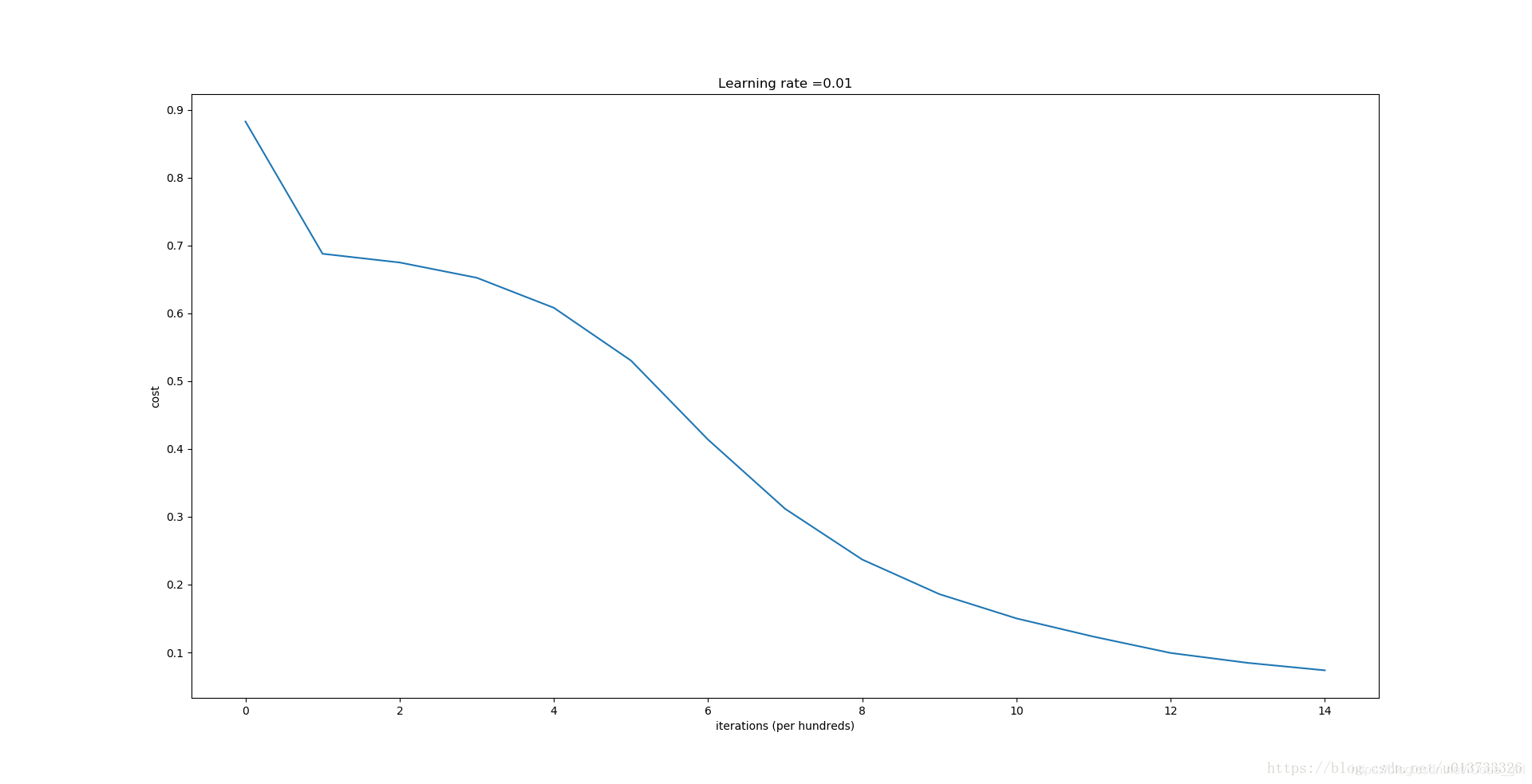
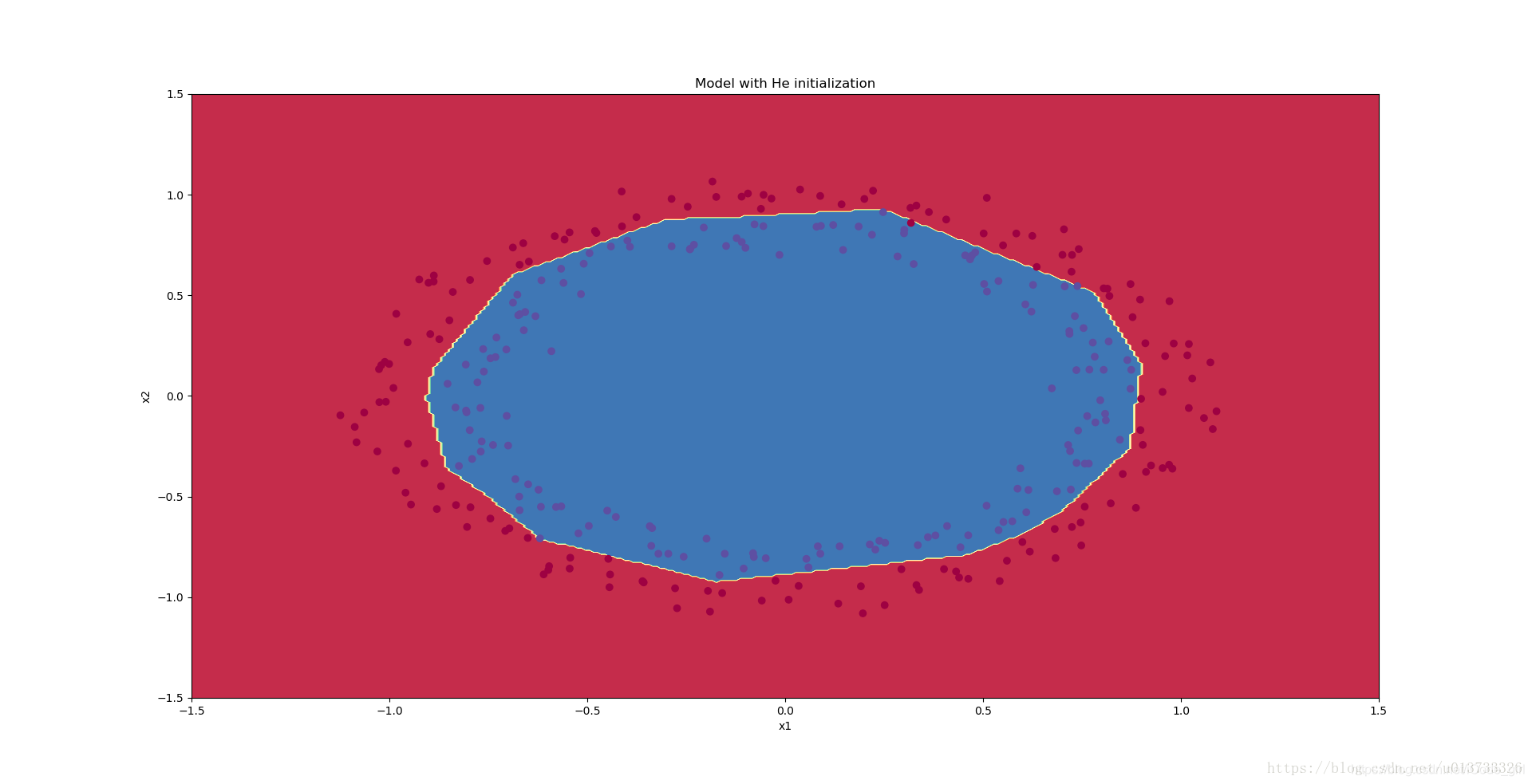
初始化的模型将蓝色和红色的点在少量的迭代中很好地分离出来

recap：

• 不同的初始化方法可能导致性能最终不同；
• 随机初始化有助于打破对称，使得不同隐藏层的单元可以学习到不同的参数；
• 初始化时，初始值不宜过大；
• He初始化搭配ReLU激活函数常常可以得到不错的效果。

2. 正则化模型

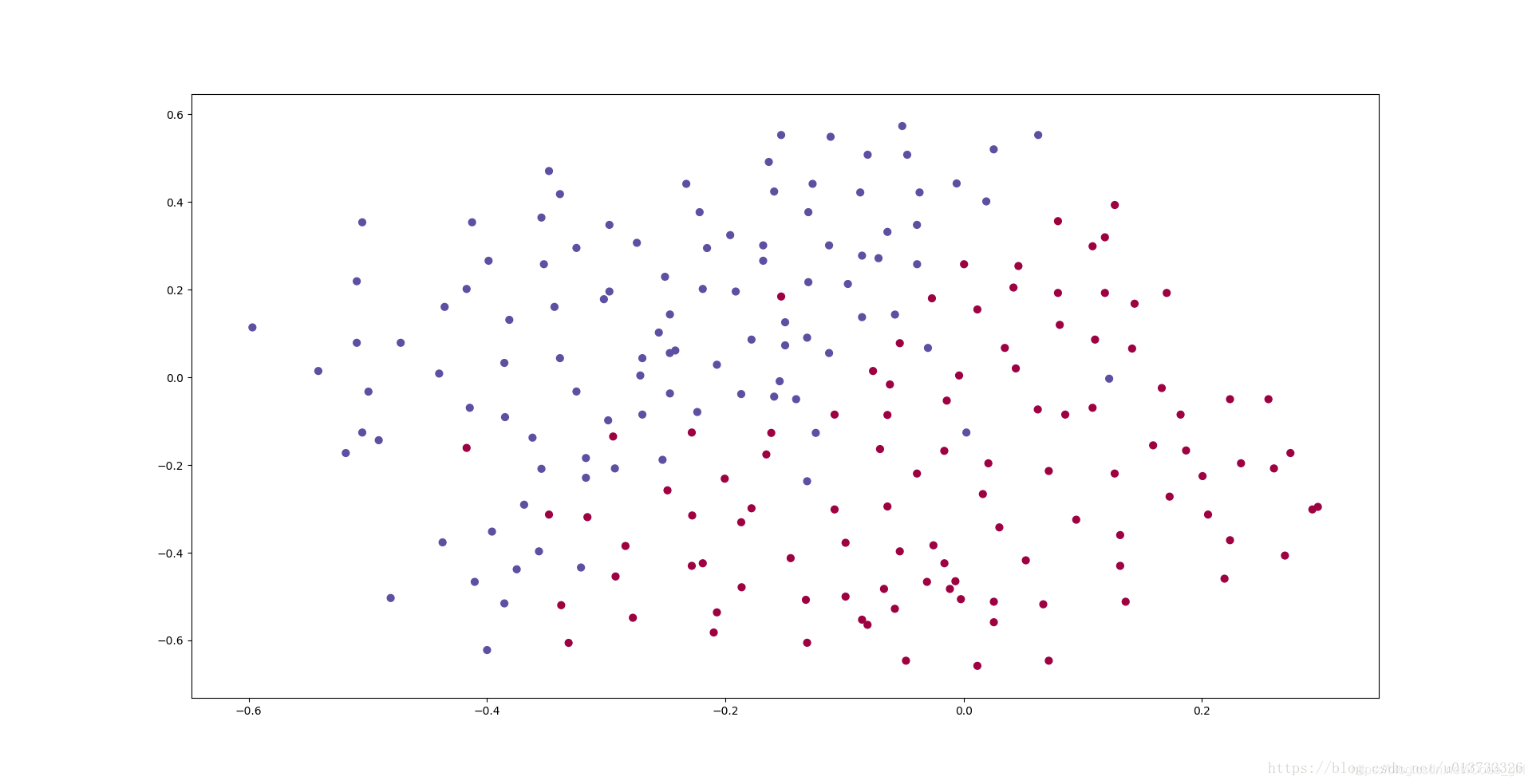
使用三种方式分类，并比较结果。

模型代码

def model(X,Y,learning_rate=0.3,num_iterations=30000,print_cost=True,is_plot=True,lambd=0,keep_prob=1):
    grads = {}
    costs = []
    m = X.shape[1]
    layers_dims = [X.shape[0],20,3,1]

    #初始化参数
    parameters = reg_utils.initialize_parameters(layers_dims)

    #开始学习
    for i in range(0, num_iterations):
        #前向传播
        ##是否随机删除节点
        if keep_prob == 1:
            ###不随机删除节点
            a3, cache = reg_utils.forward_propagation(X,parameters)
        elif keep_prob < 1:
            ###随机删除节点
            a3 , cache = forward_propagation_with_dropout(X,parameters,keep_prob)
        else:
            print("keep_prob参数错误！程序退出。")
            exit

        #计算成本
        ## 是否使用二范数
        if lambd == 0:
            ###不使用L2正则化
            cost = reg_utils.compute_cost(a3,Y)
        else:
            ###使用L2正则化
            cost = compute_cost_with_regularization(a3,Y,parameters,lambd)

        #反向传播
        ##可以同时使用L2正则化和随机删除节点，但是本次实验不同时使用。
        assert(lambd == 0  or keep_prob ==1)

        ##两个参数的使用情况
        if (lambd == 0 and keep_prob == 1):
            ### 不使用L2正则化和不使用随机删除节点
            grads = reg_utils.backward_propagation(X,Y,cache)
        elif lambd != 0:
            ### 使用L2正则化，不使用随机删除节点
            grads = backward_propagation_with_regularization(X, Y, cache, lambd)
        elif keep_prob < 1:
            ### 使用随机删除节点，不使用L2正则化
            grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)

        #更新参数
        parameters = reg_utils.update_parameters(parameters, grads, learning_rate)

        #记录并打印成本
        if i % 1000 == 0:
            ## 记录成本
            costs.append(cost)
            if (print_cost and i % 10000 == 0):
                #打印成本
                print("第" + str(i) + "次迭代，成本值为：" + str(cost))

    #是否绘制成本曲线图
    if is_plot:
        plt.plot(costs)
        plt.ylabel('cost')
        plt.xlabel('iterations (x1,000)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()

    #返回学习后的参数
    return parameters

不使用正则化

parameters = model(train_X, train_Y,is_plot=True)
print("训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("测试集:")
predictions_test = reg_utils.predict(test_X, test_Y, parameters)
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
reg_utils.plot_decision_boundary(lambda x: reg_utils.predict_dec(parameters, x.T), train_X, train_Y)

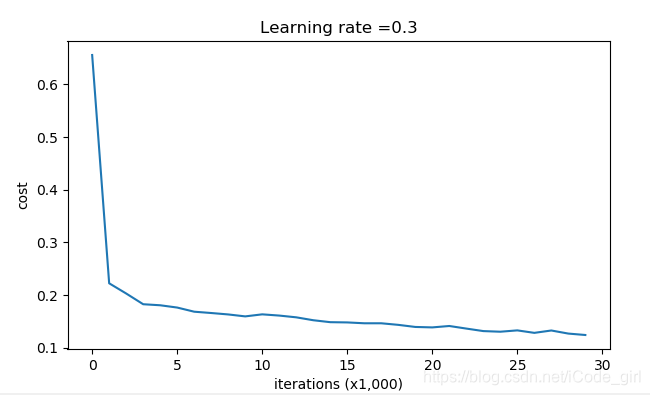
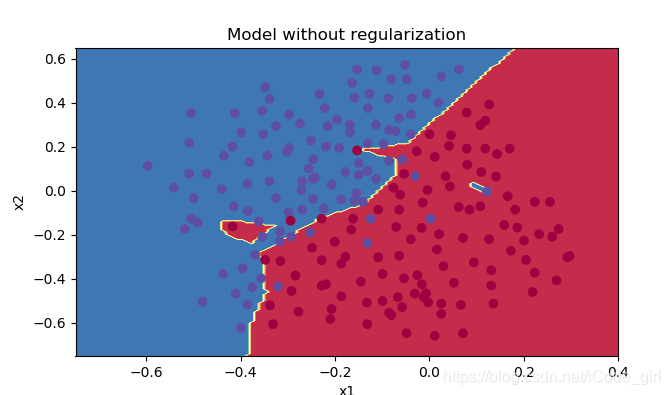
使用正则化

L2正则化

避免过度拟合的标准方法称为L2正则化，它包括适当修改你的成本函数，我们从原来的成本函数(1)到现在的函数(2)：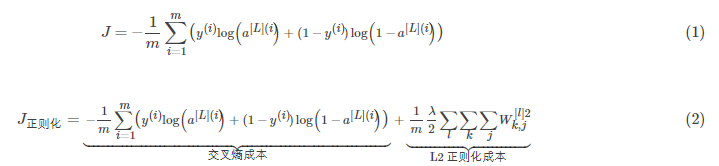
计算 $∑_k∑_jW^{[l]2}_{k,j}$的代码为：

np.sum(np.square(Wl))

相关函数

def compute_cost_with_regularization(A3,Y,parameters,lambd):
    """
    实现公式2的L2正则化计算成本

    参数：
        A3 - 正向传播的输出结果，维度为（输出节点数量，训练/测试的数量）
        Y - 标签向量，与数据一一对应，维度为(输出节点数量，训练/测试的数量)
        parameters - 包含模型学习后的参数的字典
    返回：
        cost - 使用公式2计算出来的正则化损失的值

    """
    m = Y.shape[1]
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    W3 = parameters["W3"]

    cross_entropy_cost = reg_utils.compute_cost(A3,Y)

    L2_regularization_cost = lambd * (np.sum(np.square(W1)) + np.sum(np.square(W2))  + np.sum(np.square(W3))) / (2 * m)

    cost = cross_entropy_cost + L2_regularization_cost

    return cost
#当然，因为改变了成本函数，我们也必须改变向后传播的函数， 所有的梯度都必须根据这个新的成本值来计算。

def backward_propagation_with_regularization(X, Y, cache, lambd):
    """
    实现我们添加了L2正则化的模型的后向传播。

    参数：
        X - 输入数据集，维度为（输入节点数量，数据集里面的数量）
        Y - 标签，维度为（输出节点数量，数据集里面的数量）
        cache - 来自forward_propagation（）的cache输出
        lambda - regularization超参数，实数

    返回：
        gradients - 一个包含了每个参数、激活值和预激活值变量的梯度的字典
    """

    m = X.shape[1]

    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache

    dZ3 = A3 - Y

    dW3 = (1 / m) * np.dot(dZ3,A2.T) + ((lambd * W3) / m )
    db3 = (1 / m) * np.sum(dZ3,axis=1,keepdims=True)

    dA2 = np.dot(W3.T,dZ3)
    dZ2 = np.multiply(dA2,np.int64(A2 > 0))
    dW2 = (1 / m) * np.dot(dZ2,A1.T) + ((lambd * W2) / m)
    db2 = (1 / m) * np.sum(dZ2,axis=1,keepdims=True)

    dA1 = np.dot(W2.T,dZ2)
    dZ1 = np.multiply(dA1,np.int64(A1 > 0))
    dW1 = (1 / m) * np.dot(dZ1,X.T) + ((lambd * W1) / m)
    db1 = (1 / m) * np.sum(dZ1,axis=1,keepdims=True)

    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}

    return gradients

结果：

parameters = model(train_X, train_Y, lambd=0.7,is_plot=True)
print("使用正则化，训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("使用正则化，测试集:")
predictions_test = reg_utils.predict(test_X, test_Y, parameters)
plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
reg_utils.plot_decision_boundary(lambda x: reg_utils.predict_dec(parameters, x.T), train_X, train_Y)

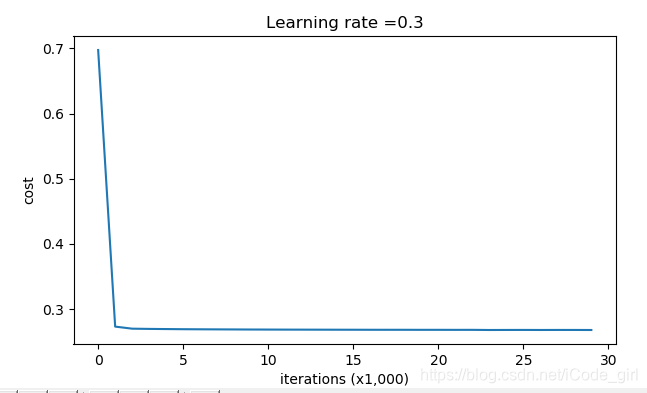
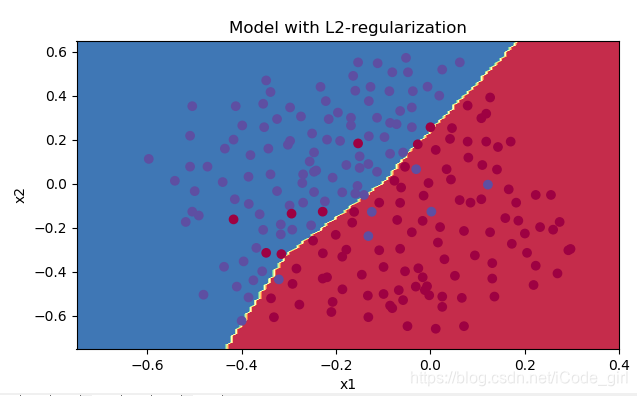
  λ的值是可以使用开发集调整的超参数。L2正则化会使决策边界更加平滑。如果λ太大，也可能会“过度平滑”，从而导致模型高偏差。
  
  L2正则化实际上在做什么？L2正则化依赖于较小权重的模型比具有较大权重的模型更简单这样的假设，因此，通过削减成本函数中权重的平方值，可以将所有权重值逐渐改变到到较小的值。权值数值高的话会有更平滑的模型，其中输入变化时输出变化更慢，但是你需要花费更多的时间。
  
L2正则化对以下内容有影响：

• 成本计算：正则化的计算需要添加到成本函数中
• 反向传播功能：在权重矩阵方面，梯度计算时也要依据正则化来做出相应的计算
• 重量变小（“重量衰减”)：权重被逐渐改变到较小的值。

dropout 正则化

Dropout的原理就是每次迭代过程中随机将其中的一些节点失效。当我们关闭一些节点时，我们实际上修改了我们的模型。背后的想法是，在每次迭代时，我们都会训练一个只使用一部分神经元的不同模型。随着迭代次数的增加，我们的模型的节点会对其他特定节点的激活变得不那么敏感，因为其他节点可能在任何时候会失效。
下面我们将关闭第一层和第三层的一些节点，我们需要做以下四步：

• 初始化一个和 $A^{[1]}$相同的随机矩阵 $D^{[1]}$。
• 如果 $D^{[1]}$低于 (keep_prob)的值我们就把它设置为0，如果高于(keep_prob)的值我们就设置为1。
• 把 $A^{[1]}$ 更新为 $A^{[1]}∗D^{[1]}$。 (我们已经关闭了一些节点)。我们可以使用 $D^{[1]}$作为掩码。我们做矩阵相乘的时候，关闭的那些节点（值为0）就会不参与计算，因为0乘以任何值都为0。
• 使用 $A^{[1]}$除以 keep_prob。这样做的话我们通过缩放就在计算成本的时候仍然具有相同的期望值，这叫做反向dropout。

def forward_propagation_with_dropout(X,parameters,keep_prob=0.5):
    """
    实现具有随机舍弃节点的前向传播。
    LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.

    参数：
        X  - 输入数据集，维度为（2，示例数）
        parameters - 包含参数“W1”，“b1”，“W2”，“b2”，“W3”，“b3”的python字典：
            W1  - 权重矩阵，维度为（20,2）
            b1  - 偏向量，维度为（20,1）
            W2  - 权重矩阵，维度为（3,20）
            b2  - 偏向量，维度为（3,1）
            W3  - 权重矩阵，维度为（1,3）
            b3  - 偏向量，维度为（1,1）
        keep_prob  - 随机删除的概率，实数
    返回：
        A3  - 最后的激活值，维度为（1,1），正向传播的输出
        cache - 存储了一些用于计算反向传播的数值的元组
    """
    np.random.seed(1)

    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]

    #LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    Z1 = np.dot(W1,X) + b1
    A1 = reg_utils.relu(Z1)

    #下面的步骤1-4对应于上述的步骤1-4。
    D1 = np.random.rand(A1.shape[0],A1.shape[1])    #步骤1：初始化矩阵D1 = np.random.rand(..., ...)
    D1 = D1 < keep_prob                             #步骤2：将D1的值转换为0或1（使​​用keep_prob作为阈值）
    A1 = A1 * D1                                    #步骤3：舍弃A1的一些节点（将它的值变为0或False）
    A1 = A1 / keep_prob                             #步骤4：缩放未舍弃的节点(不为0)的值
    """
    #不理解的同学运行一下下面代码就知道了。
    import numpy as np
    np.random.seed(1)
    A1 = np.random.randn(1,3)

    D1 = np.random.rand(A1.shape[0],A1.shape[1])
    keep_prob=0.5
    D1 = D1 < keep_prob
    print(D1)

    A1 = 0.01
    A1 = A1 * D1
    A1 = A1 / keep_prob
    print(A1)
    """

    Z2 = np.dot(W2,A1) + b2
    A2 = reg_utils.relu(Z2)

    #下面的步骤1-4对应于上述的步骤1-4。
    D2 = np.random.rand(A2.shape[0],A2.shape[1])    #步骤1：初始化矩阵D2 = np.random.rand(..., ...)
    D2 = D2 < keep_prob                             #步骤2：将D2的值转换为0或1（使​​用keep_prob作为阈值）
    A2 = A2 * D2                                    #步骤3：舍弃A1的一些节点（将它的值变为0或False）
    A2 = A2 / keep_prob                             #步骤4：缩放未舍弃的节点(不为0)的值

    Z3 = np.dot(W3, A2) + b3
    A3 = reg_utils.sigmoid(Z3)

    cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)

    return A3, cache
def backward_propagation_with_dropout(X,Y,cache,keep_prob):
    """
    实现我们随机删除的模型的后向传播。
    参数：
        X  - 输入数据集，维度为（2，示例数）
        Y  - 标签，维度为（输出节点数量，示例数量）
        cache - 来自forward_propagation_with_dropout（）的cache输出
        keep_prob  - 随机删除的概率，实数

    返回：
        gradients - 一个关于每个参数、激活值和预激活变量的梯度值的字典
    """
    m = X.shape[1]
    (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache

    dZ3 = A3 - Y
    dW3 = (1 / m) * np.dot(dZ3,A2.T)
    db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
    dA2 = np.dot(W3.T, dZ3)

    dA2 = dA2 * D2          # 步骤1：使用正向传播期间相同的节点，舍弃那些关闭的节点（因为任何数乘以0或者False都为0或者False）
    dA2 = dA2 / keep_prob   # 步骤2：缩放未舍弃的节点(不为0)的值

    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = 1. / m * np.dot(dZ2, A1.T)
    db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)

    dA1 = np.dot(W2.T, dZ2)

    dA1 = dA1 * D1          # 步骤1：使用正向传播期间相同的节点，舍弃那些关闭的节点（因为任何数乘以0或者False都为0或者False）
    dA1 = dA1 / keep_prob   # 步骤2：缩放未舍弃的节点(不为0)的值

    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1. / m * np.dot(dZ1, X.T)
    db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)

    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}

    return gradients

结果：

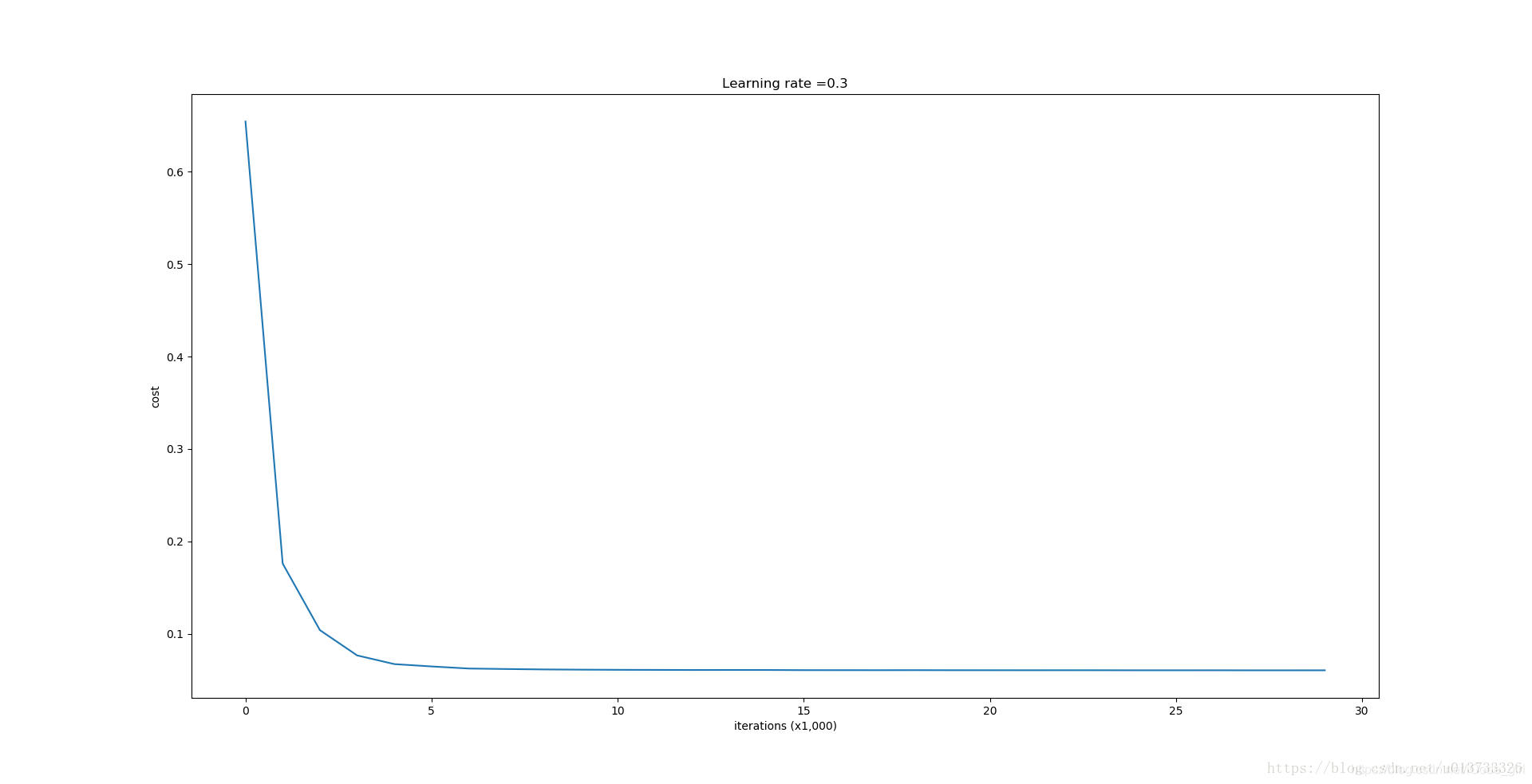
parameters = model(train_X, train_Y, keep_prob=0.86, learning_rate=0.3,is_plot=True)
print("使用随机删除节点，训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("使用随机删除节点，测试集:")
reg_utils.predictions_test = reg_utils.predict(test_X, test_Y, parameters)

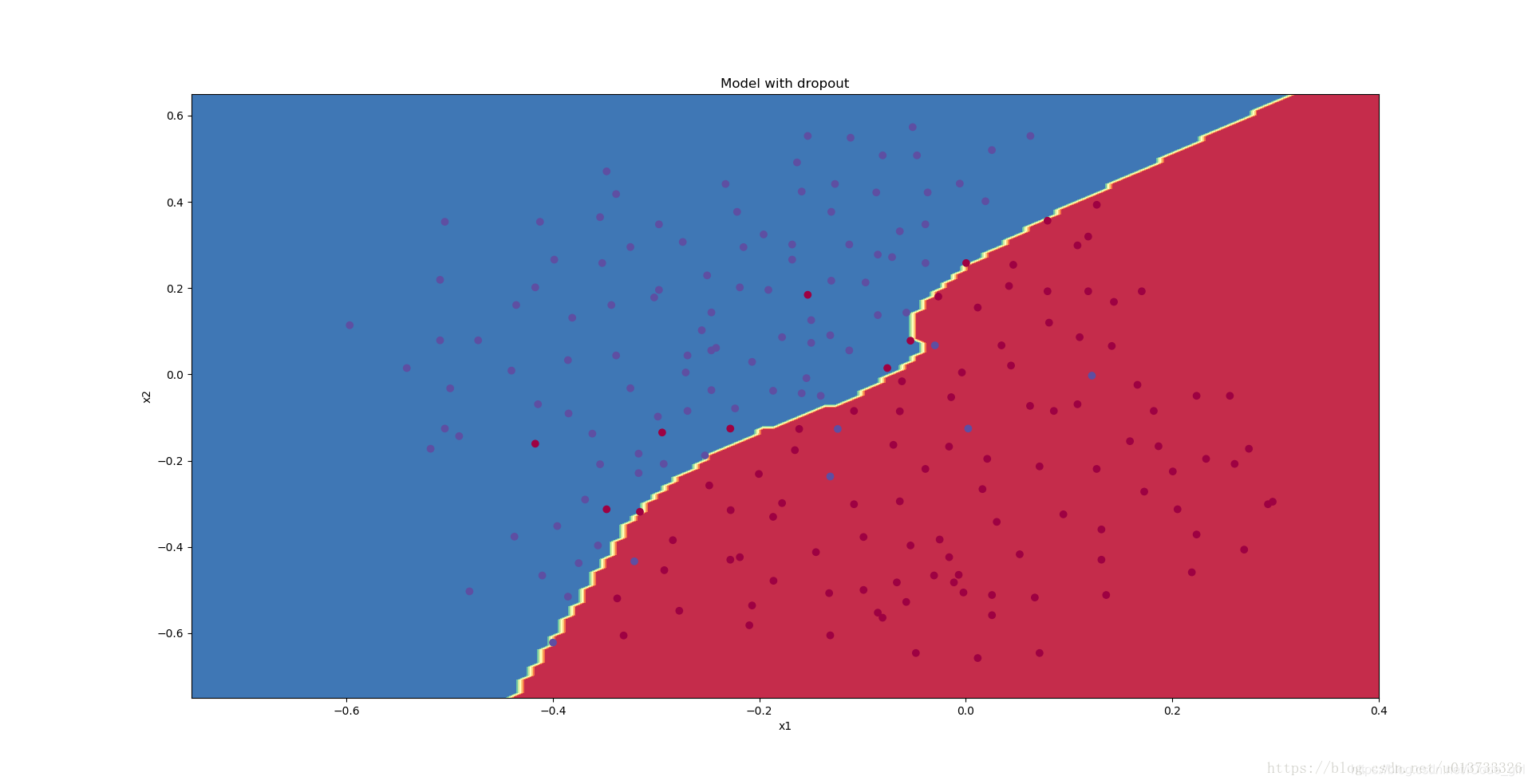
plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75, 0.40])
axes.set_ylim([-0.75, 0.65])
reg_utils.plot_decision_boundary(lambda x: reg_utils.predict_dec(parameters, x.T), train_X, train_Y)

3. 梯度校验

def forward_propagation_n(X,Y,parameters):
    """
    实现图中的前向传播（并计算成本）。

    参数：
        X - 训练集为m个例子
        Y -  m个示例的标签
        parameters - 包含参数“W1”，“b1”，“W2”，“b2”，“W3”，“b3”的python字典：
            W1  - 权重矩阵，维度为（5,4）
            b1  - 偏向量，维度为（5,1）
            W2  - 权重矩阵，维度为（3,5）
            b2  - 偏向量，维度为（3,1）
            W3  - 权重矩阵，维度为（1,3）
            b3  - 偏向量，维度为（1,1）

    返回：
        cost - 成本函数（logistic）
    """
    m = X.shape[1]
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]

    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    Z1 = np.dot(W1,X) + b1
    A1 = gc_utils.relu(Z1)

    Z2 = np.dot(W2,A1) + b2
    A2 = gc_utils.relu(Z2)

    Z3 = np.dot(W3,A2) + b3
    A3 = gc_utils.sigmoid(Z3)

    #计算成本
    logprobs = np.multiply(-np.log(A3), Y) + np.multiply(-np.log(1 - A3), 1 - Y)
    cost = (1 / m) * np.sum(logprobs)

    cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)

    return cost, cache

def backward_propagation_n(X,Y,cache):
    """
    实现图中所示的反向传播。

    参数：
        X - 输入数据点（输入节点数量，1）
        Y - 标签
        cache - 来自forward_propagation_n（）的cache输出

    返回：
        gradients - 一个字典，其中包含与每个参数、激活和激活前变量相关的成本梯度。
    """
    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache

    dZ3 = A3 - Y
    dW3 = (1. / m) * np.dot(dZ3,A2.T)
    dW3 = 1. / m * np.dot(dZ3, A2.T)
    db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)

    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    #dW2 = 1. / m * np.dot(dZ2, A1.T) * 2  # Should not multiply by 2
    dW2 = 1. / m * np.dot(dZ2, A1.T)
    db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)

    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1. / m * np.dot(dZ1, X.T)
    #db1 = 4. / m * np.sum(dZ1, axis=1, keepdims=True) # Should not multiply by 4
    db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)

    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
                 "dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
                 "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}

    return gradients

梯度校验：

def gradient_check_n(parameters,gradients,X,Y,epsilon=1e-7):
    """
    检查backward_propagation_n是否正确计算forward_propagation_n输出的成本梯度

    参数：
        parameters - 包含参数“W1”，“b1”，“W2”，“b2”，“W3”，“b3”的python字典：
        grad_output_propagation_n的输出包含与参数相关的成本梯度。
        x  - 输入数据点，维度为（输入节点数量，1）
        y  - 标签
        epsilon  - 计算输入的微小偏移以计算近似梯度

    返回：
        difference - 近似梯度和后向传播梯度之间的差异
    """
    #初始化参数
    parameters_values , keys = gc_utils.dictionary_to_vector(parameters) #keys用不到
    grad = gc_utils.gradients_to_vector(gradients)
    num_parameters = parameters_values.shape[0]
    J_plus = np.zeros((num_parameters,1))
    J_minus = np.zeros((num_parameters,1))
    gradapprox = np.zeros((num_parameters,1))

    #计算gradapprox
    for i in range(num_parameters):
        #计算J_plus [i]。输入：“parameters_values，epsilon”。输出=“J_plus [i]”
        thetaplus = np.copy(parameters_values)                                                  # Step 1
        thetaplus[i][0] = thetaplus[i][0] + epsilon                                             # Step 2
        J_plus[i], cache = forward_propagation_n(X,Y,gc_utils.vector_to_dictionary(thetaplus))  # Step 3 ，cache用不到

        #计算J_minus [i]。输入：“parameters_values，epsilon”。输出=“J_minus [i]”。
        thetaminus = np.copy(parameters_values)                                                 # Step 1
        thetaminus[i][0] = thetaminus[i][0] - epsilon                                           # Step 2        
        J_minus[i], cache = forward_propagation_n(X,Y,gc_utils.vector_to_dictionary(thetaminus))# Step 3 ，cache用不到

        #计算gradapprox[i]
        gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)

    #通过计算差异比较gradapprox和后向传播梯度。
    numerator = np.linalg.norm(grad - gradapprox)                                     # Step 1'
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)                   # Step 2'
    difference = numerator / denominator                                              # Step 3'

    if difference < 1e-7:
        print("梯度检查：梯度正常!")
    else:
        print("梯度检查：梯度超出阈值!")

    return difference

参考资料

以上内容全部参考自吴恩达深度学习编程作业中文笔记连载：https://blog.csdn.net/u013733326/article/details/79847918