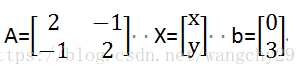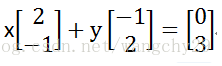麻省理工线性代数第一讲

麻省理工线性代数第一讲

本文主要发表个人学习麻省理工线性代数公开课的学习心得。

---

课程第一讲，讲师花费了接近40分钟的时间，我觉得其实主要就是想说明三点：

1. 方程组的几何意义
2. 方程组的矩阵向量表示形式
3. 方程组解存在问题

几何意义

2x - y = 0
-x + 2y = 3
考虑上述方程组，在几何上方程组的解即为直线2x-y=0和直线-x+2y=3的交点。
2x - y = 0
-x + 2y - z = -1
0x - 3y + 4z= 4
而如果是上述方程组，则可以理解为三个平面在三维空间上的交点。

矩阵向量表示

方程组的系数可以看成一个矩阵A，成为系数矩阵，未知数可以看成列向量X，方程组右侧常数值看成一个列向量b，则AX=b。如下：
2x - y = 0
-x + 2y = 3
则：

如果将其写成这样则可以理解为求解一组列向量，使其满足AX=b.
如果写成下图这样，

将系数矩阵按列拆分，每一列是一个列向量，依次成为列向量1，2。则可以理解为寻找一个列向量1和列向量2的线性组合，使其满足结果为b。结合上文的几何意义来看，就是要在二维空间看，哪对x和y可以让x倍的向量1与y倍的向量2的和为b。

解存在问题

对于上述方程组的向量b，我们很容易看出x=1,y=2满足条件，但是如果只考虑AX=b，是否对任意的b，我们都能寻找到一个满足条件的X呢？
是否存在一个满足条件的解，从几何意义上看，上述二元方程组的解是否存在则意味着每个方程组对应的直线否交于一点，对三元方程组来说，则是每个方程组对应的平面是否交于一点。
从向量的角度来看，就是是否存在一个由系数矩阵拆分出来的列向量组的线性组合使得结果满足b。如果组成系数矩阵的列向量相互独立且列向量数目不少于空间维度，则可以生成空间内任意的b，即对任意b，方程组有解。