参考资料:
网易公开课:http://open.163.com/special/opencourse/daishu.html 麻省理工公开课:线性代数
一、矩阵乘法
假设:$A$为$m\times n$矩阵,$B$为$n\times p$矩阵,$AB=C$,$C$为$m\times p$矩阵
(1)逐个元素$C_{ij}$求解公式
$$C_{ij}=\sum_{k=1}^{n}A_{ik}B_{kj}$$
(2)逐列求解$C_{:,j}$:$C$每一列$C_{:,j}$为$A$的列的线性组合,组合系数由$B$的每一列决定
(3)逐行求解$C_{i,:}$:$C$每一行$C_{i,:}$为$B$的行的线性组合,组合系数由$A$的每一行决定
(4)整列乘以整行:先分别将矩阵$A$的各列($m\times 1$)与矩阵$B$的各行($1\times p$)相乘得到$m\times p$的秩1矩阵,再求和
$$C=\sum_{k=1}^{n}A_{\color{red}:,k}B_{k,\color{red}:}$$
(5)分块乘法
![]()
二、矩阵的逆(矩阵可逆或非奇异时存在):
假设$A$为方阵,相应的逆矩阵为$A^{-1}$
(1)性质:$A^{-1}A=I=AA^{-1}$
(2)高斯-约旦消元法(求解逆矩阵:$A^{-1}[A~|~I]=[A^{-1}A~|~A^{-1}I]=[I~|~A^{-1}]$)
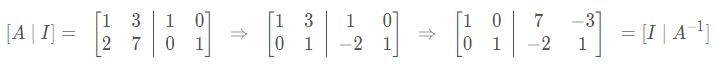
注:将左侧的矩阵$A$变换为单位矩阵$I$,则右侧的单位矩阵$I$会变为逆矩阵$A^{-1}$
(3)奇异矩阵(不可逆):存在非零向量$\mathbf{x}$使得$A\mathbf{x}=0$,即奇异矩阵可以通过各列的非零线性组合得到零向量