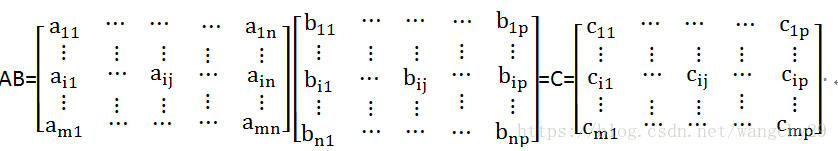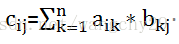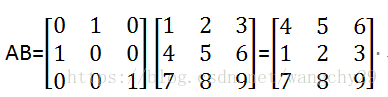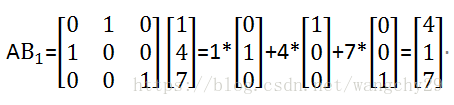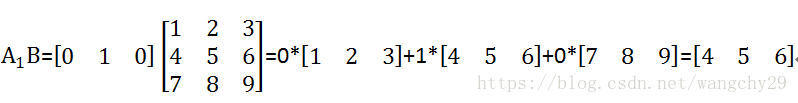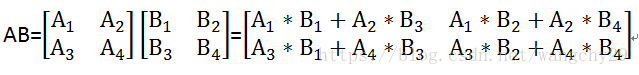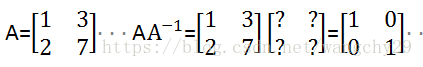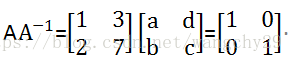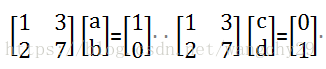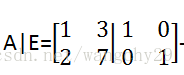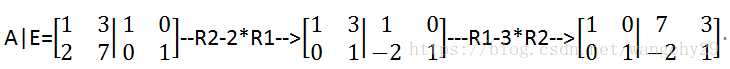麻省理工线性代数第三讲

课程第三讲的核心内容主要包括两部分：

1. 矩阵乘法
2. 逆矩阵

矩阵乘法##

首先矩阵A可以与B相乘的条件是A的列数等于B的行数，即当A为mn矩阵，B为sp矩阵时，只有n=p才能计算AB，下面用A为mn矩阵，B为np矩阵讲解矩阵相乘的运算。

1. 元素法
   
   如上图A，B，C均用元素来表示，则Cij的计算公式为：
   
   如
   其中C21=a21b11+a22b21+a23*b31=2
2. 列向量
   这种方法类似第二讲中所讲，根据左行右列，将矩阵B按列拆分成P个列向量，依次乘在A的右边形成第一列、第二列……第p列。
   同样对于上述矩阵，将B拆分成3个列向量，这里只考虑第一个列向量
   
   后面两个列向量同理。
3. 行向量
   这种方法同样类似第二讲中所讲，根据左行右列，将矩阵A按行拆分成m个行向量，乘在B的左边，分别形成结果的第一行，第二行……第m行。以A的一个行向量为例。
   
4. 矩阵分块
   矩阵分块的方法就是将AB矩阵分别分块成若干矩阵，再进行相乘，当然分块后相乘的矩阵必须满足相乘的条件。
   如图:
   
   其中Ai*Bj的运算可用上面三种方法，当然对矩阵的分块并非只有一种，视情况而定。

逆矩阵

可逆矩阵的条件：第二讲已经介绍**存在一组初等变换矩阵使得该组矩阵乘方阵A可与得到单位矩阵时，矩阵A可逆，称A为可逆矩阵，而不满足条件的矩阵称为奇异矩阵。**注：可逆矩阵一定是方阵。
这讲讲师补充到不存在不为零的X使得AX=0的矩阵A可逆。
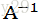
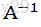
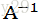
可逆矩阵A的逆为而且A=A=E
此时证明为何可逆矩阵必定不存在一个非零向量X使得AX=0，假设存在一个非零向量X，满足AX=0，在等式左端乘上A的逆矩阵，则根据上述矩阵与逆矩阵的特征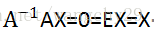，，而X不是零向量，因此矛盾，假设不成立。
如何求逆矩阵？？本讲主要介绍两种方法。

1. 设未知数解方程组

第一种方法是最简单粗暴的方法，设未知数解方程组。
假设：

此时只需要为将方阵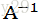的每个元素设成未知数，解方程组即可。

2. 高斯-若尔当方法

同样求解上述矩阵A的逆，相当于求解两个方程组，如下图：

这种方法可以同时求解两个方程：

方法就是将A和E放在一起考虑，组合成一个增广矩阵，然后通过矩阵变换将矩阵A变成E，而直线后面的矩阵就是要求得逆矩阵。

经检验所得矩阵确实为A的逆矩阵。