自然语言处理基础之信息熵，交叉熵，相对熵

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/weixin_40449129/article/details/90264500

本文主要介绍信息论基本相关知识，这些知识在机器学习中的相关算法的基础，是学习机器学习及深度学习的基础知识。本文具体介绍信息熵、交叉熵及相对熵，需要深入了解信息论知识，请参考《信息论基础》。

1）信息熵（Information Entropy）

       信息熵来源于克劳德·爱尔伍德·香农的信息论，在介绍信息熵之前，我们先来了解信息量的概念。
       人类交流可以理解信息的交流。你接收的任何一条信息，都包含一定的信息量，只是每条信息对应的信息量可能会有不同。比如国兵取得奥运会金牌，国足取得世界杯总冠军等都包含一些信息量，但它们包含的信息量不同。由于国足取得世界杯总冠军这个事件的概率很小，需要确认这个事件，你需要了解很多的信息，所以国足包含的信息量更大。因此，信息量是用来确定一件事情所需要的信息量的大小，某事件发生的概率小，则该事件的信息量大，信息量与事件发生的概率成反比（1）。
       如果我们有两个不相关的事件 x 和 y，那么观察两个事件同时发生时获得的信息量应该等于观察到事件各自发生时获得的信息之和。
                                           $I(x,y) = I(x) + I(y)$（2）
       因为两个事件是独立不相关的，因此必须满足 $p(x,y)=p(x)p(y)$ （3）
       根据以上三个要求，香农构造自信息函数 $I(X)$为：
                                           $I(x) = log(\frac{1}{p(x)}) =-logp(x)$
        $I(x)$ 自信息 (self-information)函数图像如下：

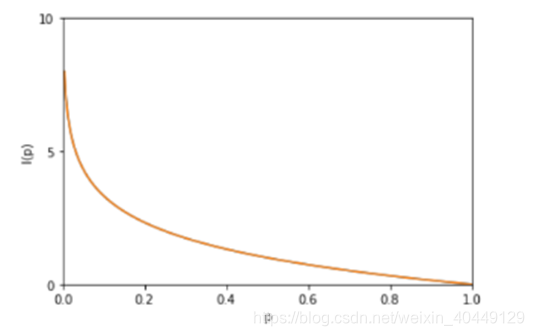
       对随机变量的信息量求期望即为信息熵（Information Entropy）,它是表示随机变量不确定的度量，是对所有可能发生的事件产生的信息量的期望。
                      $H(x) = -\sum_{x}p(x)log(p(x))=-\sum_{i=1}^{n}p(x_i)log(p(x_i))$
       随机变量的取值个数越多，状态数也就越多，信息熵就越大，混乱程度就越大。当随机分布为均匀分布时，熵最大， $且 0≤H(X)≤logn$。如事件满足伯努利分布时，熵的函数图像如下，当概率都为0.5时，熵最大，等于1：

2）相对熵（Relative Entropy）/KL散度（Kullback-Leibler Divergence）

       相对熵用于衡量两个概率分布之间的差异。假设 p(x)、q(x) 是 离散随机变量 X 中取值的两个概率分布，则 p 对 q 的相对熵为：
                                           $D_K(p||q)=\sum_{x}p(x)log\frac{p(x)}{q(x)}=E_plog\frac{p(x)}{q(x)}$

• $D_K(p||q)≥0 ，证明如下（利用Jensen不等式证明）$

• 相对熵具有不对称性， $D_K(p||q) 不等于D_K(p||q)$，因此便有了Average KL，公式如下：
                                      $AKL(p||q) =\frac{D_K(p||q) + D_K(q||p)}{2}$

• p(x) 和 q(x) 两个分布越相近，相对熵越小，当p(x) 和 q(x) 两个分布相同，相对熵等于0。因此，

3）交叉熵（Cross Entropy）

       交叉熵同样也用于描述两个概率分布之间的差异。假设样本集A其背后的真实分布为 p(x) ， 我们假设样本集A的分布为q(x) 。如果用真实分布 p(x) 来衡量识别别一个样本所需要编码长度的期望（平均编码长度），即p(x)的信息熵：
                      $H(p) = -\sum_{x}p(x)log(p(x))$
       如果使用假设的分布 q(x) 来表示来自真实分布 p(x) 的平均编码长度，即用q(x)来表示p(x)的分布：
                      $H(p,q) = -\sum_{x}p(x)log(q(x))$
以上即为交叉熵的定义。
       下面我们对交叉熵的公式进行简单变换：
                      $H(p,q) =H(p(x))+D_k(p||q)$
推导过程如下：

       在机器学习中，我们是不知道数据的真实分布，因此我们希望在训练数据上模型学到的分布 P(model) 和真实数据的分布 P(real) 越接近越好，所以我们可以使其相对熵最小，因此交叉熵被用于逻辑回归的Sigmoid和深度学习Softmax函数作为损失函数是有一定道理的。

（欢迎转载，转载请注明出处。）