封面镇楼

目录
一、熵
对于离散型随机变量,当它服从均匀分布时,熵有极大值。取某一个值的概率为1,取其他所有值的概率为0时,熵有极小值(此时随机变量退化成确定的变量)。对于离散型随机变量,假设概率质量函数为p(x),熵是如下多元函数 :
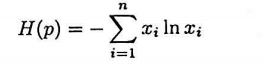
伯努利分布的熵为:
![]()
对于连续型随机变量,假设概率密度函数为p(x),熵(也称为微Differential Entropy分熵 )定义为:

性质: 对于离散型随机变量,当他服从均匀分布时,熵有极大值。取某一个值的概率为1,其他所有值的概率为0时,熵有极小值
二、联合熵
联合熵(Joint Entropy)是熵对多维概率分布的推广,它描述了一组随机变量的不确定性。以二维随机向量为例,有两个离散型随机变量X和Y,它们的联合概率质量函数为p(x),联合熵定义为:

推广到多个随机变量,有:

对于连续型随机向量(X,Y),假设联合概率密度函数为p(x,y),其联合熵为二重积分

对于n维连续型随机变量x,假设联合概率密度函数为p(x), 其联合熵为二重积分:
![]()
三、相对熵(KL散度)
相对熵(Relative Entropy)也称为KL散度(Kullback-Leibler Divergence),用于衡量两个概率分布之间的差异。其值越大,则两个概率分布的差异越大;当两个概率分布完全相等时相对熵值为0。对于两个离散型概率分布p和g,它们之间的相对熵定义为:

其中p(x)和q(x)为两个概率分布的概率质量函数。
两个伯努利分布之间的相对熵:

对于两个连续概率分布p和q,他们的相对熵:

性质一:相对熵非负,对于任意两个概率分布p和q,下面不等式成立,下式也称Gibbs不等式:
![]()
性质二:当且仅当两个概率分布相等,相对熵取得最小值0。
性质三:相对熵不具有对称性,即:
![]()
四、交叉熵
交叉熵是数学期望,也用于衡量两个概率分布之间的差异,其值越大,两个概率分布差异越大;其值越小,两个概率分布差异越小。对于离散型随机变量:

对于两个连续型随机变量,加啥概率密度函数分别为p(x)和q(x),交叉熵定义为:

性质一: 如果两个概率分布完全相等,则交叉熵退化成熵。
性质二:交叉熵不是距离,不具有对称性,也不满足三角不等式。
性质三:当两个概率分布相等时,交叉熵有极小值。
性质四:交叉熵与相对熵的关系。交叉熵与相对熵都反映了两个概率分布的差异程度,下面推导他们的关系:

因此相对熵等于交叉熵与熵之差,如果p(x)已知,则其熵H(p)为常数。在机器学习中通常以概率分布p(x)为目标,拟合出一个概率分布q(x)。此时H(p)是常量,所以通常直接优化H(p,q)就可以了。
五、JS散度
Jensen-Shannon散度定义于两个概率分布上,根据KL散度构造,同样描述了两个概率分布的差异,且具有对称性。JS散度定义如下:
![]()
其中概率分布m为p和q的均值:
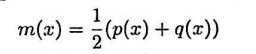
性质一:JS散度是非负的,JS散度越大,两个概率分布之间的差异越大。
性质二:JS散度具有对称性
性质三:当且仅当两个概率分布相等时,JS散度等于0

![]()
六、互信息
互信息定义了两个概随机变量的依赖程度。它可以看成是一个随机变量中包含的关于另一个随机变量的信息量,或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。对于两个离散型随机变量X和Y,他们的互信息:

其中p(x,y)为X和Y的联合概率,p(x)和q(x)分别为X和Y的边缘概率。互信息反映了联合概率p(x,y)与边缘概率乘积的差异程度。如果两个随机变量独立,则p(x,y) = p(x)*p(y),因此他们越接近于相互独立,则p(x,y)和 p(x)*p(y)的值越接近。换句换说互信息越接近于0,两个随机变量越独立。
对于两个连续随机变量X和Y,他们的互信息定义如下:

性质一:互信息是非负的;互信息越大,两个概率分布之间的依赖程度越强;两个概率分布互相独立时,互信息等于0。
性质二:与熵的关系。推导过程省略,直接说结论。
![]()
两个随机变量的联合熵等于它们各自的熵减去互信息,这与集合运算的规律类似,互信息可以看作两个随机变量信息量的重叠部分,如下图所示。图中两个椭圆区域分别为两个随机变量的熵H(X)和H(Y),它们重叠的部分为这两个随机变量之间的互信息I(X,Y),两个圆的并集为它们的联合熵H(X,Y)。

七、条件熵
条件熵是给定X的条件下Y的条件概率p(y|x)的熵H(Y|X=x)对X的数学期望,对离散型概率分布,公式为:

其中p(x,y)为X和Y的联合概率, p(x)为X的边缘概率,条件熵与联合熵的公式非常相似,只是对数函数多了一个分母,这里约定0*ln0 / 0 = 0 且 0*lnc / 0 = 0, c>0.
条件熵的直观含义是根据随机变量X的取值x将整个数据集划分成多个子集,每个子集内的x相等,计算这些子集的熵,然后用p(x)作为权重系数,对子集的熵进行加权平均。
性质:根据条件熵与联合熵的定义,有:

因此 的条件熵H(YIX)是它们的联合熵H(X,Y)与熵H(X)的差值。
下图形象反映了熵、条件熵、联合熵和互信息的关系

八、总结
