量子傅里叶变换
一开始看到这个题目我是这样的:
然后我开始了有关傅里叶变换的学习,我从某站上面截了一张图:顺便附上某站的链接,视觉上很享受。
形象展示傅里叶变换


一.傅里叶级数
在开始这一个部分的讲述时,先了解两个傅里叶级数的推导所涉及的两个关键。
1.三角函数系的正交性
在高中的时候,我们涉及到过两个向量的点乘,当它们的点乘为0,这两个向量垂直(正交);在学习了线性代数之后,向量的正交性被推广到了n维;在学了一点量子力学之后,线性代数中常用的实数向量变为了复数向量(矢量),从而引入了希尔伯特空间;而到了现在,当看到了三角函数系这一个名词,可能首先会想到系列这个词,的确,三角函数系就是一系列的正余弦函数:
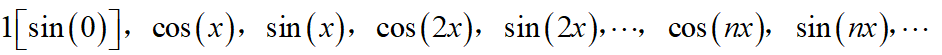
这样一个序列的函数的正交性是指其中的任意两个不同的函数的乘积在给定闭区域[- π \pi π, π \pi π]的积分为0,这是类似于量子计算中的正交归一基的,比如: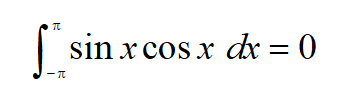
了解了三角函数系的正交性之后,再来了解一下欧拉公式。
2.欧拉公式
欧拉公式是把复指数函数和三角函数联系到一起的一个公式,如果学过电路分析,你会知道正弦的相量表示法,看到里面是怎样将复数与三角函数联系在一起的;学过高等数学,你会知道在解一个二阶的常系数微分方程时如何将复值函数的解转换为实值函数的解,这是一个神奇的公式,在我看来,虚数的出现就已经够神奇了,据说起初是为了解一个一元三次方程然后解出了一个根号下有负数的情形,后来笛卡尔给出了虚数这个名词,意为不存在的数,直到很久以后虚数这个名词才被接受。扯的有点远了,欧拉公式很神奇(尽管我不是学数学的,但简洁的东西是真的看着舒坦),看一看下面这个式子:
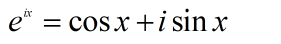
转换一下:
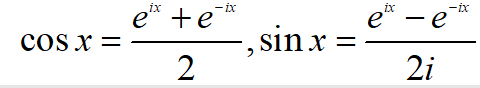
当x= π \pi π时,可以得到一个显得更简洁的式子:
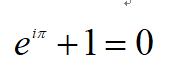
当然,用起来可能就没那么简单了。
更新:与欧拉公式有联系的那些数学知识:
- 棣莫弗定理
我这里终点强调这个定理的乘方形式,即:
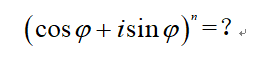
棣莫弗定理告诉我们:
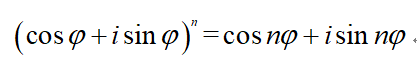
表现为指数形式就是:
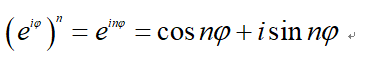
这可以通过数学归纳法进行证明. - 泰勒展开
通过对泰勒公式和级数的学习,我们可以知道如下展开式:
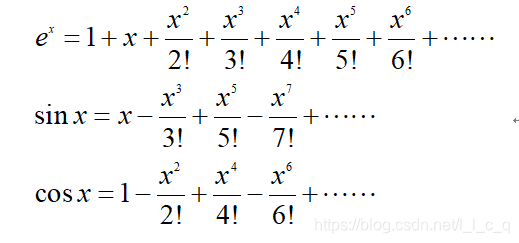
上面的x是属于实数R的,可是如果x可以在复数C中取呢?然后我们可以得到:
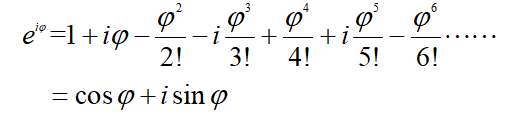
现在,我们大概知道欧拉公式怎么来的了。
3.傅里叶级数
对于一个函数f(x),若有:
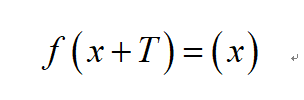
则该函数总可以用一系列以T为周期的正弦函数组成的无穷级数来表示,即:
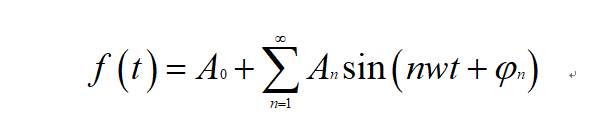
从上面的式子,我们可以看到,这是一个以T=2 π \pi π/w为周期的函数,现在,我们将其拆开得到:
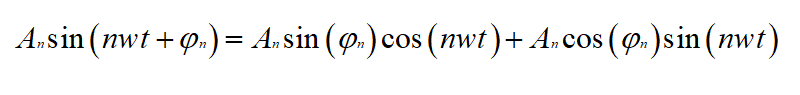
接下来,我们令w= π \pi π/l,(即T=2l),A0=a0,an=An sin \sin sin φ \varphi φn,bn=An cos \cos cos φ \varphi φn,t=x得到:
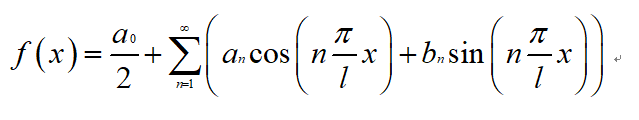
然后我们给定区间[-l,l],将上式等号两边同时在这个范围积分,由于三角函数系的正交性,可以得到:
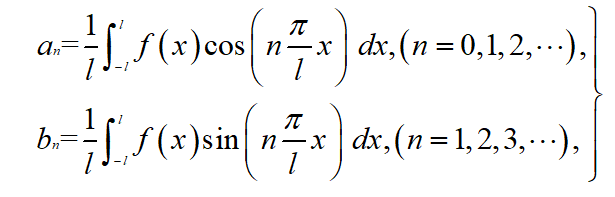
这只是实数形式的,接下来使用欧拉公式将其转换为复数形式的,则上面的f(x)的傅里叶级数为:
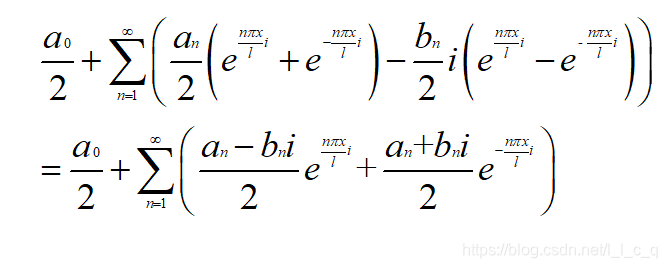
现在令c0=a0/2,cn=(an-bni )/2,c-n=(an+bni )/2,从而傅里叶级数的复数形式可以简单地表示为:
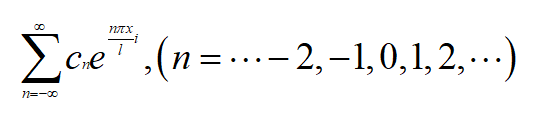
到这里已经差不多了,至于周期函数的傅里叶级数的收敛性质,如有兴趣可以去书上看一下。
在之后,我会开始介绍傅里叶变换。
二.傅里叶变换
1.时域和频域
如果是第一次接触这个名词,一定会和我刚开始学习一样分不清傅里叶级数和傅里叶变换实际上,他们两个合在一起就是傅里叶分析,傅里叶分析将时域和频域贯穿,现在先简单理解一下,当我们看视频时,随着屏幕下方的进度条的移动,屏幕的画面不断变换,这就是时域,而频域就是随着频率发生变化一个频率的幅值会随之变化,原谅一个初学者的知识浅薄,难以用更好的语言去描述频域。但我想到了大学物理里面的振动方程和波动方程,一个振动方程描述了一个质点的位置随着时间变化而发生变化,能够体现相位的变化情况,一个波动方程描述了多个质点的震动情况,但是无法得知相位的变化情况,简单来说,振动方程的y-t图可以看作时域,y-x图可以近似看作频域(如果把x当作频率的话),一个更好的例子就是音乐,这个例子也是我通过看某一篇文章知道的。
这是时域:

这是频域(瞧瞧上面跳动的音符在不同频率的位置和正余弦的振幅的联系):

我很喜欢那篇文章里的一句话:
你眼中看似落叶纷飞变化无常的世界,实际只是躺在上帝怀中一份早已谱好的乐章!
这句话很美不是吗?所以我也附上了那篇文章的链接:
对于一个傅里叶分析的初学者再合适不过的文章了,有你喜欢的骚话
关于时域和频域,我借用一下那篇文章里的图一下,毕竟那张图把时域和频域表达得很清楚:
另外需要注意的是,傅里叶级数是时域表达式,而傅里叶变换是频域表达式。
2.傅里叶变换
相比之前的傅里叶级数,傅里叶变换相当于是把周期函数的周期取无穷大然后再对其傅里叶级数求极限;傅里叶级数是时域的表达方式,而傅里叶变换是频域的表达方式,并且是完全的频域分析,它能够将时域映射到频域。傅立叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号。比如一个麦克风在接受声音时得到是不同振幅和不同频率的正弦波的合成,那么问题的核心在于如何将这个合成的声音分解为原来的样子,这样的变换叫做傅里叶变换,而将不同振幅和不同频率的正弦波再合成的这种变换叫做逆傅里叶变换。
傅里叶变换公式:
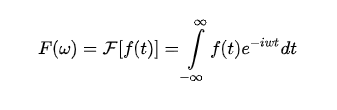
逆傅里叶变换公式:
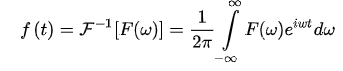
3.应用与现象
有关傅里叶变换的应用比如收音机,接受信息的时候如果不经过调频是听不到什么有用的内容的,而调了频之后,你才能听到有用的信息。收音机接受的相当于是所有电台特有频率的正弦波的合成信息,调了频之后就可以过滤掉其他没用的频率的正弦波了。
有关傅里叶变换的现象比如牛顿做的那个三棱镜实验,三棱镜就相当于对白光做了一次傅里叶变换,然后将白光分解为各种不同频率的红橙黄绿蓝靛紫光。
傅里叶所做出的的贡献是世所共睹的,尽管我才了解了一点点粗浅的东西,依旧能感觉到上面两个公式的强大,科学家才是真正值得人敬佩的不是吗?我觉得我需要再找本书好好看一下傅里叶分析才能更深入理解傅里叶变换。
三.量子傅里叶变换
直到现在才开始文章标题的内容,实在感慨于自身基础的薄弱,不过还好,开心学习嘛!量子傅里叶变换是一种量子门,可用于Shor算法,既然是一种量子门,那么它必有一种矩阵表示,其n个量子比特的矩阵表示为:
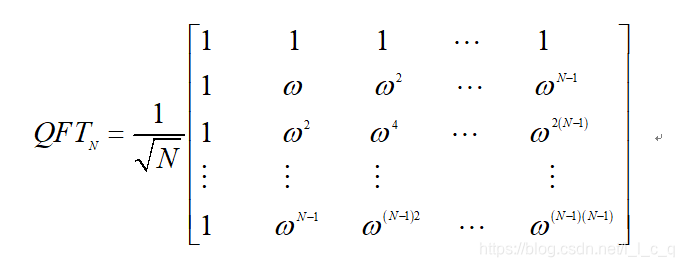
其中
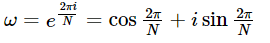
然后让其作用于一组右矢:

这意味着当我们按照顺序输入幅值:
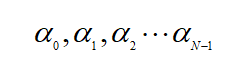
就会输出幅值:
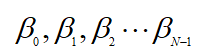
四.复数
在虚数诞生没多久,谁会想到,曾经的虚数走到了这个地步。复数在线性代数和量子力学中用的很多,为此,我需要在我那原先对复数浅薄的理解之上再添加点东西。
开始,我们知道i= − 1 \sqrt-1 −1,然后就知道复数和复平面的存在,再接着是共轭复数,这些都是高中就学过的东西。对于一个i,现在你还可以想到什么?旋转!在复平面里的任意一个复数,只要它乘以i,该复数就会逆时针旋转90度,除以i则顺时针旋转90度。
对于指数形式的复数。例如ei Θ \Theta Θ在复平面内表示一个与实轴正向夹角为 Θ \Theta Θ的向量,把 Θ \Theta Θ换为时间t,当时间t从零开始变为2 π \pi π,这个向量就从实轴正方向逆时针旋转了360度。把 Θ \Theta Θ换为 ω \omega ωt,那么e ω \omega ωt i的图像就可以观察到旋转的频率。
复数的存在导致的旋转还体现在矩阵的线性变换中,比如有一个具有复特征值的实矩阵,这个矩阵可以分解出导致实数向量旋转的矩阵,比如设一个矩阵 A= [ a − b b a ] (2) \left[ \begin{matrix} a & -b \\ b & a \\ \end{matrix} \right] \tag{2} [ab−ba](2)
其特征值为 λ \lambda λ=a+bi,令r=| λ \lambda λ|,则矩阵 A 可以分解为:
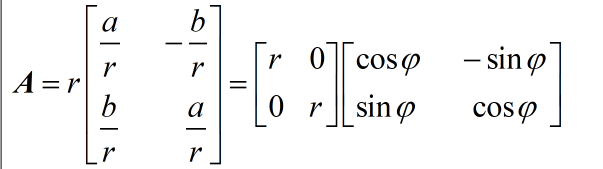
对于最右边的那个矩阵,我想学过线性代数的同学都很清楚吧,它的作用就是把其作用的向量逆时针旋转角度 φ \varphi φ。
而且对于在复平面的一个点,我们有三种表达方式:
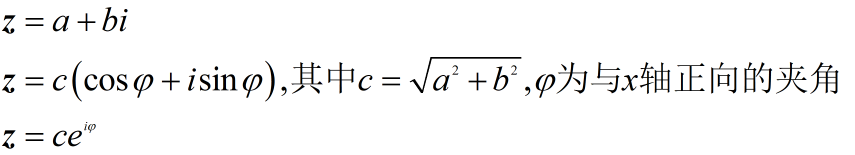
五.总结
对于这篇文章,我发现我的叙述并不能像很多大佬一样讲的随心应手,甚至可以说我觉得我的叙述有点空洞无力,我觉得是因为我基础太差,积累的太少,导致我在叙述一些知识与概念时有点乏力,希望下次有所进步,与君共勉!