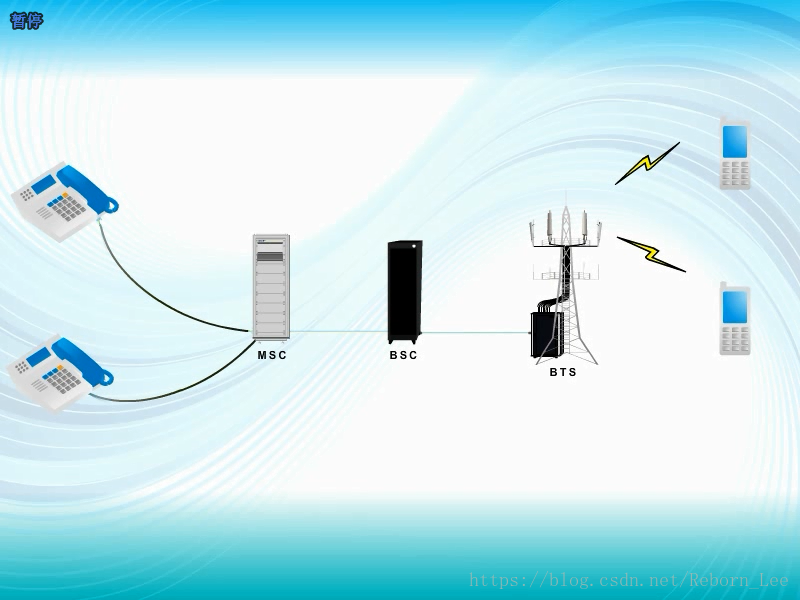
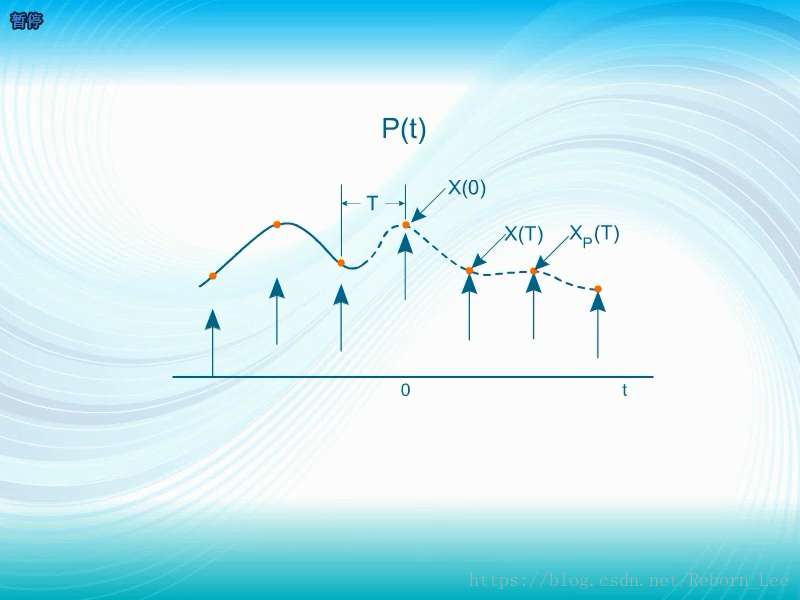
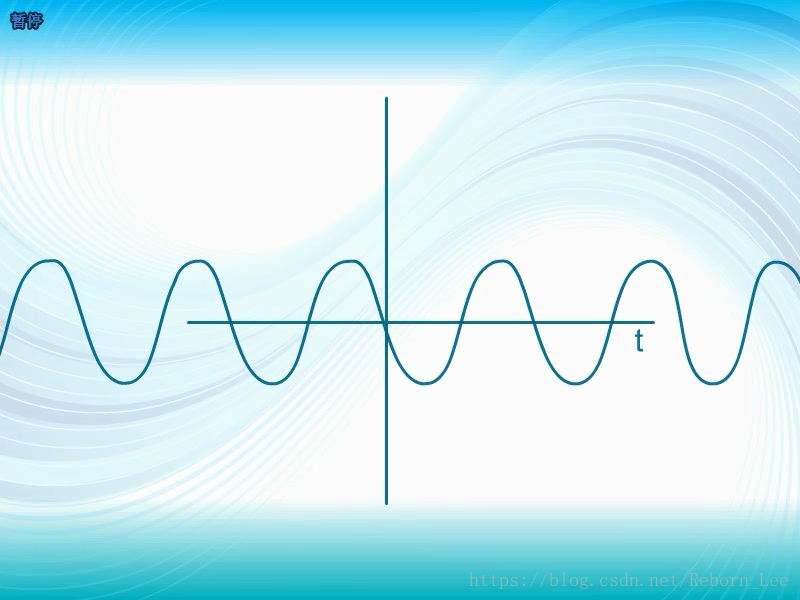
通信中的信号通常是时间的函数。
下面通过强度、频率、相位、能量来了解信号(正如通过人的五官去了解人):
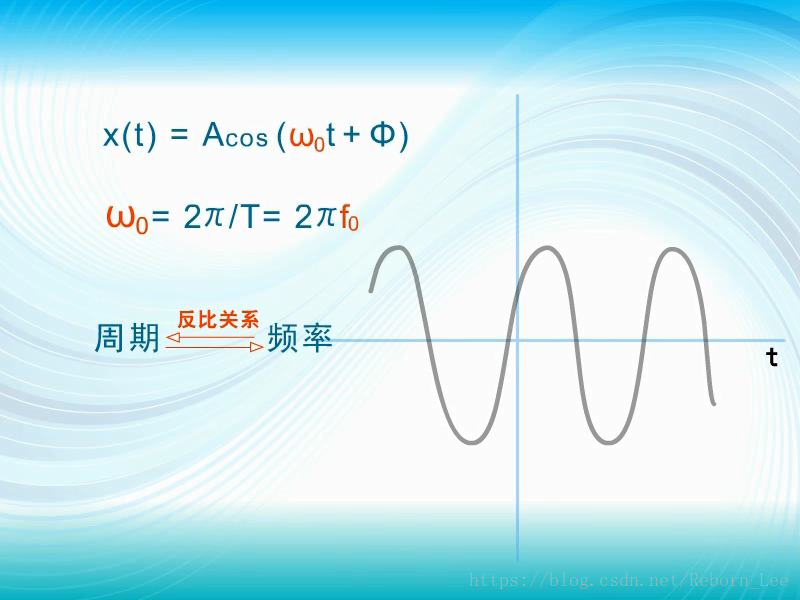
正弦信号:
周期信号的傅里叶级数:
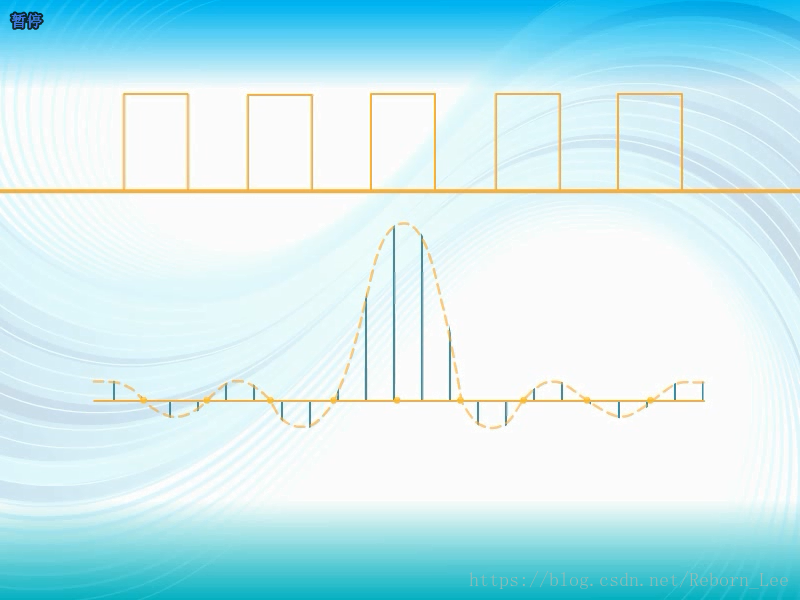
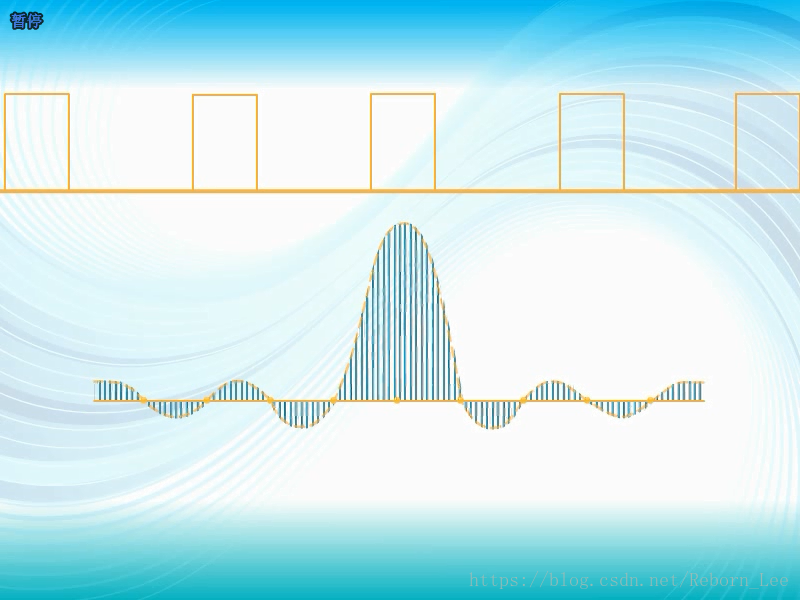
用正弦信号逼近方波:
如下图:船的振荡频率为 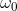
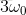

事实上,任何周期信号都能够由不同谐波的正弦波叠加而成,这由傅里叶发现,因此称之为傅里叶级数,如下图:

由复指数和正弦函数的关系,即欧拉公式可知,上式还可以如下表示:
如此以来应用更加方便;
下图为信号的频谱图:
其中a0, a1, a2, ..., 称之为傅里叶系数,信号x(t)的频谱系数,以及谐波的幅度;频谱系数表示各频率分量在总信号中所占的分量。在频谱图中可以看出,频谱系数可以表示各频率分量的强度。
综上所述,周期信号的频谱是离散谱。
非周期信号的傅里叶变换:
傅里叶认为,既然周期信号可以用正弦信号来表示,那么非周期信号也可以用正弦信号来逼近。原因是非周期信号可以看成是周期无限大的周期信号;事实证明,傅里叶的想法是对的,于是才有了大名鼎鼎的傅里叶变换。
如下图示:解释周期无限扩大后,傅里叶级数如何表示;
周期和频率成反比的关系,周期无限变大,频率间隔就会无限减小,逼近连续:
这种逼近连续的叠加,在数学上用积分表示:
形象解释积分:
例如求一个不规则的图像的面积,就要将不规则的图形分解为规则的图像进行面积叠加:
分的越细,求解越精确:
积分的意义就是把对象分得无限小再求和,分的过程叫微分,加的过程叫积分。
下面比较傅里叶级数和傅里叶变换:我们关心的是红圈部分;
著名的傅里叶变换和反变换公式:
通信中常用的信号:
正弦信号,方波信号,周期冲击串的作用:
正弦信号往往作为调制的载波出现:
方波信号是大多数数字信号的波形:
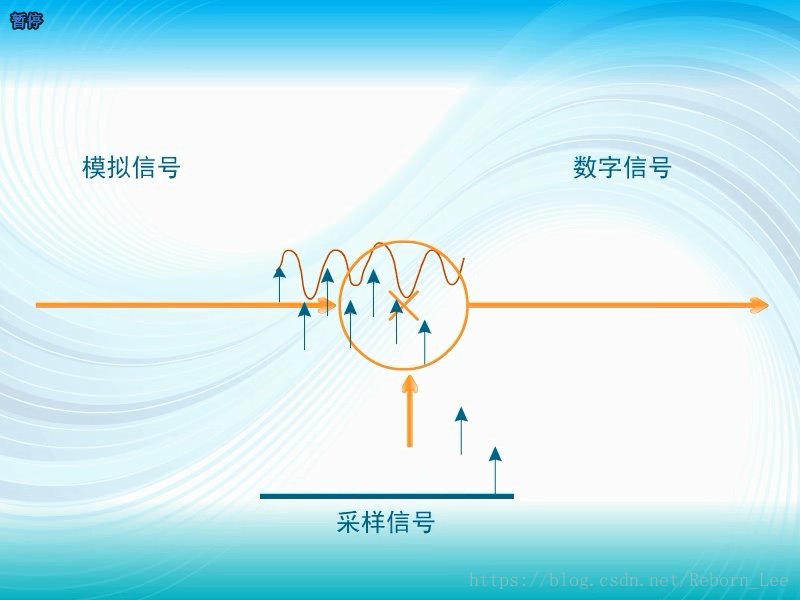
而冲击串往往作为采样信号,在模拟信号转换为数字信号的过程中扮演着重要的角色:
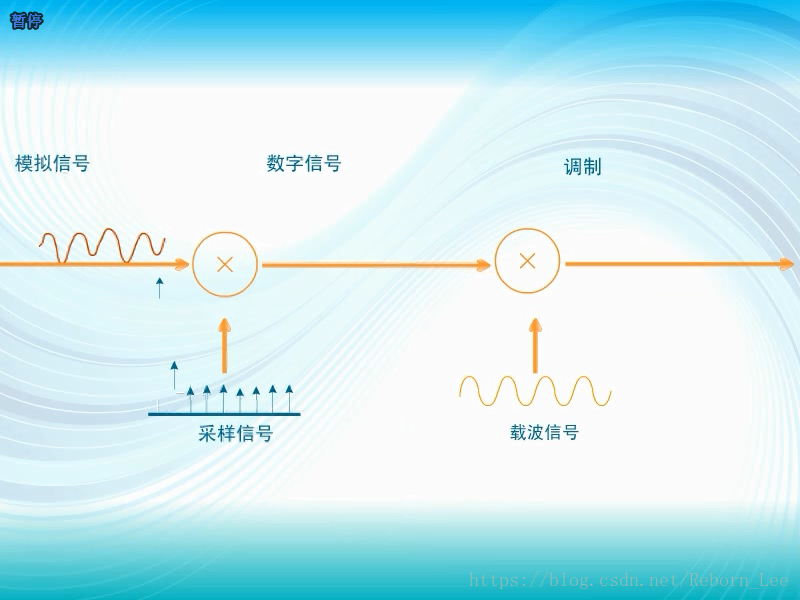
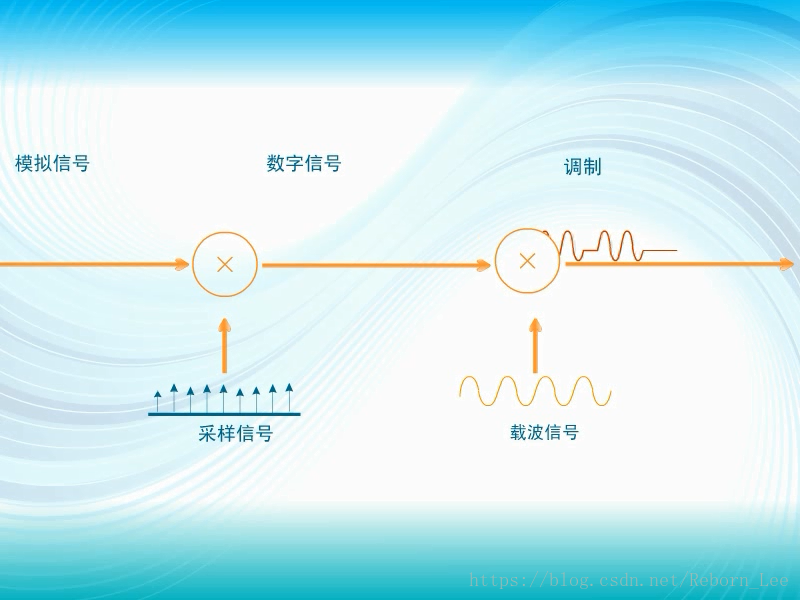
三者合起来的过程:模拟信号经过采样等过程变成数字信号,数字信号进行调制得到调制信号;
常见信号的频谱:
余弦信号的频谱,正弦信号的频谱:
周期方波的频谱:
方波周期无限扩大时,得到非周期方波的频谱:
冲击串的频谱:
用卷积解决两信号相乘的傅里叶变换:
时域相乘,频域卷积:
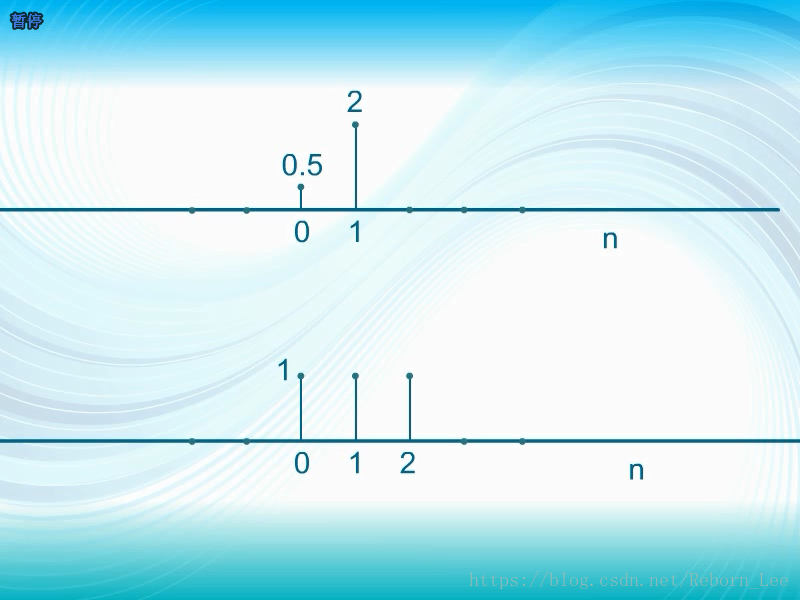
卷积定义:卷积是一种运算,如下的移位相乘再求和的过程;
例解卷积:
卷积的估算:
连续信号的卷积:
模拟信号之间卷积后,左右频率分别为原来的频率值相加,从图上看,频谱扩展了,这也是扩频通信的基本原理。
上述过程在通信的应用;
调制:
调制的目的在于通信系统中,各种信道(双绞线,同轴电缆,电磁波)对信号的频率要求不同,所传输的信号的频率不一定满足要求,所以需要将信号的频率调制到不同的范围,以适应各种传输信道。
此过程就像将汽车开到轮船上以渡海一样:
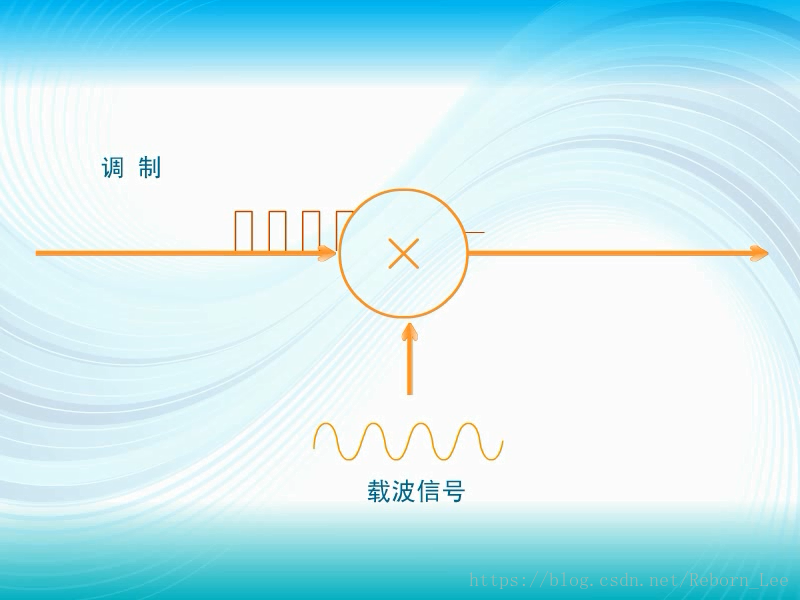
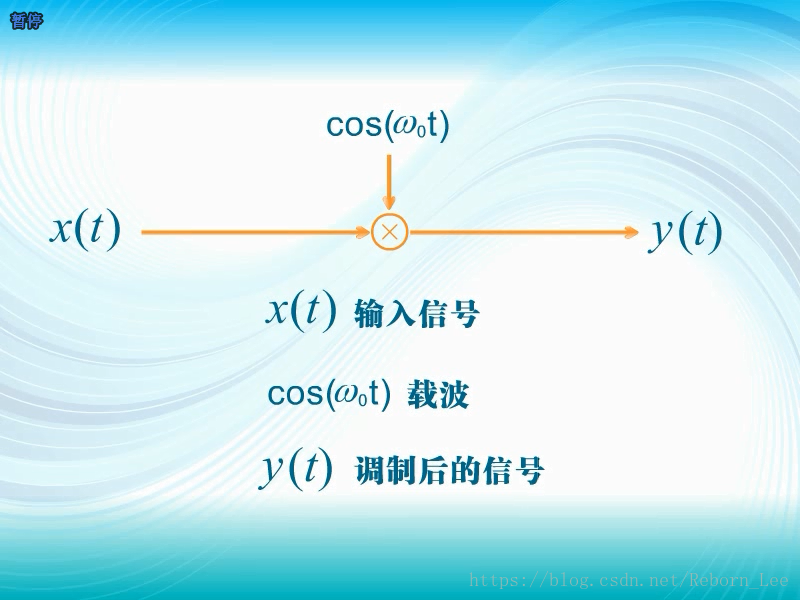
调制在电路中是通过乘法器来实现的;
调制后的信号就是输入信号和载波的乘积;
在频率就是卷积;
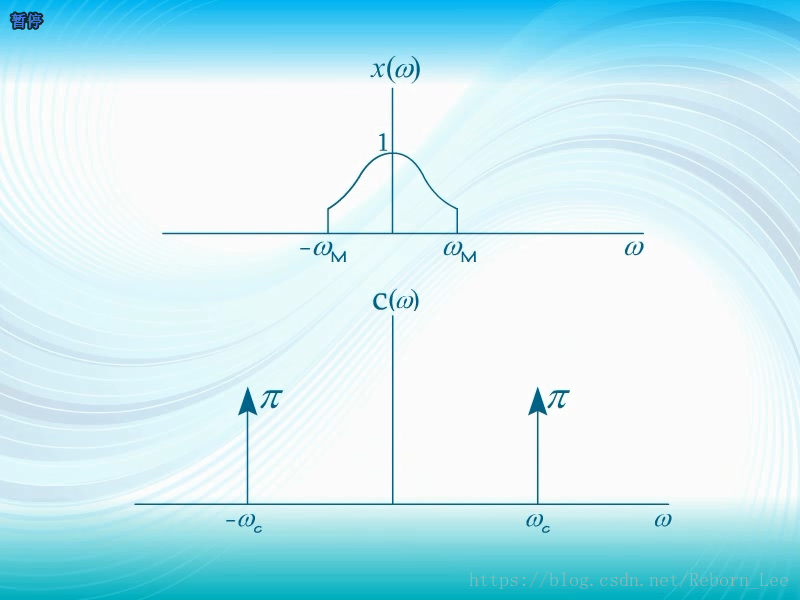
如下图:
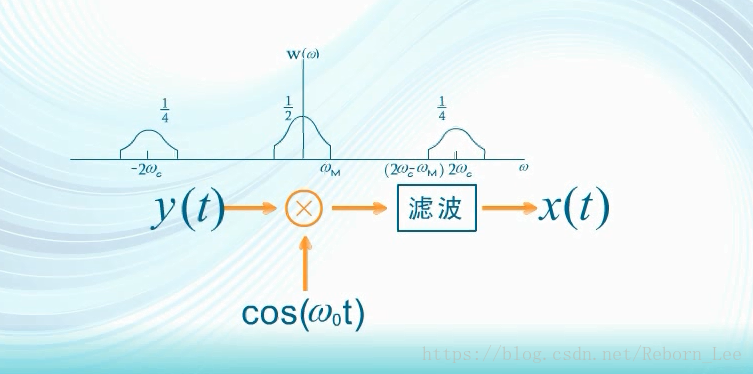
卷积后的频谱:
调制电路又称为频谱搬移电路:
解调电路:
滤波器简介:
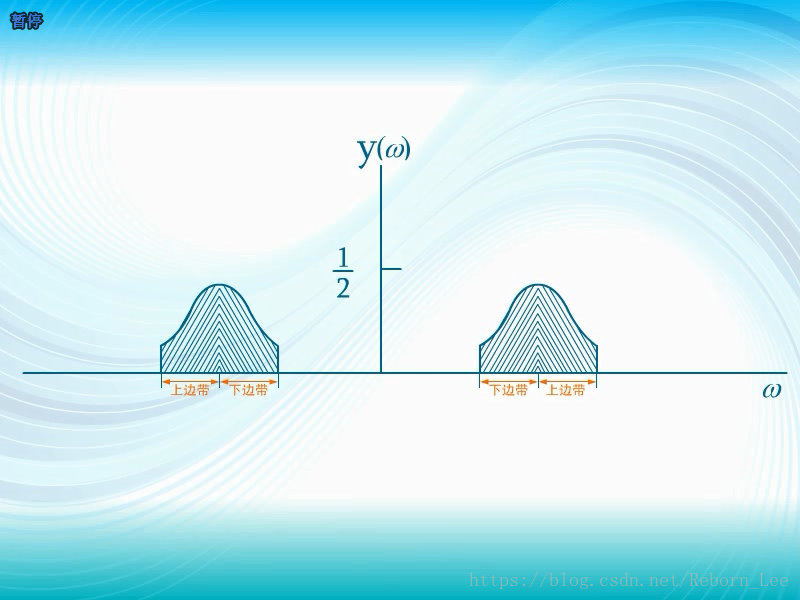
单边带调制:
将载频两边的频谱分别称为上边带和下边带。
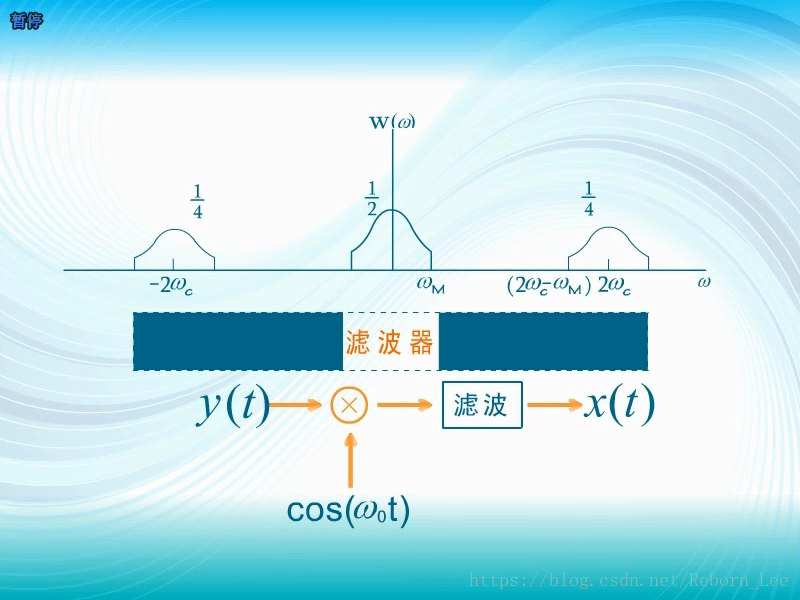
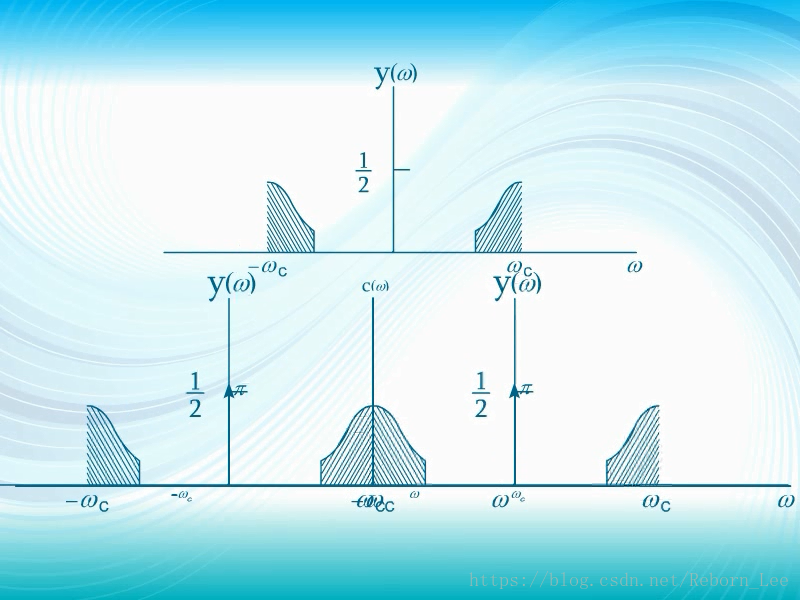
通过解调过程可以发现,其实只需要单边带,我们也可以解调出原始信号:
这就是说在已调信号中存在多余的频谱,如果去掉多余的频谱仅仅保留下边带,或者上边带,也能解调出原始信号,如此频带和发射机功率的使用都会更加经济有效:
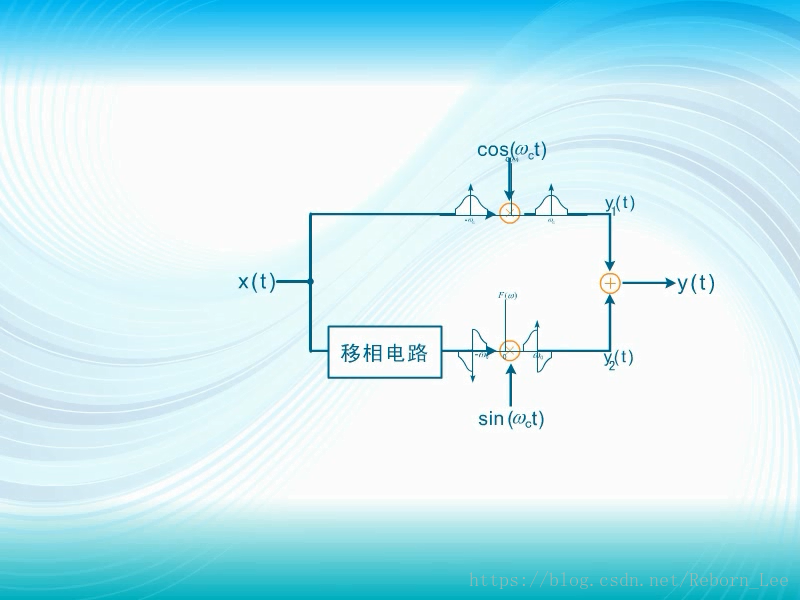
如何去掉多出的边带?
实现电路:
采样介绍:
采样电路实现:
利用这样的一串样本值能不能恢复出原始信号呢?
不能恢复的原因在于采样间隔的大小?采样间隔多大合适?我们从频域中寻找答案:
从采样频谱图中看,采样频率必须大于被采样信号最高频率的2倍。
信号的功率:
归一化功率定义为:信号在单位电阻上消耗的功率。
通信中的信号为时间的函数,因此信号的功率为瞬时功率,瞬时功率的积分即为能量。
如果上述积分存在,则称之为能量信号;
积分不存在,如下:
定义:
这种能量无限,但平均功率有限的信号称为功率信号,通常,周期信号都是功率信号。