线性代数观点来看傅里叶级数和傅里叶变换

UTF8gbsn

傅里叶级数和傅里叶变换都是十分重要的数学工具.但是学习起来也有一定的难度.写本文的目的是想以一种更为直观的角度来理解这种变换.我们采用的观点是来自于线性代数的.所以我们有必要从线性代数开始.

基本定义

在线性代数中,有一个非常重要的概念叫做正交.比如 $(1,0,0)$与 $(0,1,0)$就是互相正交的向量.而正交向量的点积为0.也就是说 $(1,0,0)\cdot (0,1,0)=0$.
我们可以看到正交的概念十分简单明了.但是实际上正交的概念更为普遍,不只是线性代数中才有的概念.更为抽象的定义是如果你定义某种操作函数K,如果 $K(a,b)=0$,我们就可以称为a,b正交.所以我们可以在三角函数中定义正交的概念.

三角函数中的正交

这里我们先列出来正交的三角函数有 $1, cos(x), sin(x), cos(2x), sin(2x),\cdots, cos(nx), sin(nx), \cdots$.这些函数在 $[-\pi, \pi]$上正交.也就是说,

$\int_{-\pi}^{\pi}{cos(nx)dx}=0$ $\int_{-\pi}^{\pi}{sin(nx)dx}=0$
$\int_{-\pi}^{\pi}{sin(kx)cos(nx)dx}=0$
$\int_{-\pi}^{\pi}{sin(kx)sin(nx)dx}=0,(k\neq n)$
$\int_{-\pi}^{\pi}{cos(kx)cos(nx)dx}=0,(k\neq n)$

我们来看看类比,对于向量 $\mathbf{a}=\left( \begin{array}{cccc} a_1 & a_2 & \cdots & a_n \end{array} \right),\mathbf{b}=\left( \begin{array}{cccc} b_1 & b_2 & \cdots & b_n \end{array} \right)$我们定义的K操作为 $K(a,b)=a_1b_1+a_2b_2+\cdots+a_nb_n$.那么对于三角函数而言,K操作定义为
$K(cos(kx),sin(nx))=\int_{-\pi}^{\pi}{cos(kx)sin(nx)dx}$
所以我们可以对于三角函数建立正交关系.我们来类比一下.

向量空间 vs 三角函数的正交空间

• 基向量

  • 向量空间中(假如这个空间的维度为n),我们把这个空间称为A
    我们可以定义基向量为 $e_1=(1,0,\cdots,0)$
    $e_2=(0,1,\cdots,0)$ $\vdots$ $e_n=(0,0,\cdots,1)$

  • 对于三角函数的空间里面我们可以定义的一组基为,我们也把这个空间称为B
    $n_1=1$ $n_2=cos(x)$ $n_3=cos(2x)$ $\vdots$
    $n_n=cos((n-1)x)$ 由这些基组成的空间,它是一个n维的三角函数空间

• 空间中任意一个向量

  • n维向量空间A $v=k_1e_1+k_2e_2+\cdots+k_ne_n$

  • 刚才提到的三角函数空间B $f=k_01+k_1c_1+\cdots+k_{n-1}c_{n-1}$
    $f=k_0+k_1cos(x)+k_2cos(2x)+\cdots+k_{n-1}cos((n-1)x)$

如何求系数

• 向量空间中如何求坐标.也就是基向量的系数.比如
  $v=k_1e_1+k_2e_2+\cdots+k_ne_n$
  这个向量的系数(坐标)是多少呢?通过上式你可以很容易观察得到坐标为 $\left( k_1, k_2, \cdots, k_n \right)$.但是实际生活中,你并不知道上面的形式,你知道 $v$而不知道 $v$怎么由 $\left( e_1, e_2, \cdots, e_n \right)$构成的.

  我们的问题变成,已知 $v$,和 $\left( e_1, e_2, \cdots, e_n \right)$,求 $v$在 $\left( e_1, e_2, \cdots, e_n \right)$这组基下面的坐标.在线性代数中,这个问题其实很简单.我们只需要用 $e_i$去点积 $v$即可.

  $k_i=v\cdot e_i$

  这样就可以求出在 $\left( e_1, e_2, \cdots, e_n \right)$下, $v$的坐标.因为 $e_i\cdot e_j=0,(i\neq j)$

• 三角函数空间

  类似的我们如果已知函数 $f(x)$由如下的三角函数组成
  $1, cos(x),sin(x),cos(2x),sin(2x),\cdots,cos(nx),sin(nx)$

  但是你不知道 $f(x)$对应这些三角函数的具体系数.你该如何做?类似于向量空间的方法,使用三角函数中定义的点积来求出对应系数 $k_i$

  比如我们要来求出 $cos(ix)$的系数,我们可以使用
  $\int_{-\pi}^{\pi}f(x)cos(ix)dx=k_i^{(cos)}\int_{-\pi}^{\pi}{cos(ix)cos(ix)dx}$

  这是应为正交的关系,所以只剩下一项了.又因为我们知道

  $\int_{-\pi}^{\pi}{cos^2(ix)dx}=\int_{-\pi}^{\pi}{\frac{cos(2ix)+1}{2}dx}=\int_{-\pi}^{\pi}{\frac{cos(2ix)}{2}dx}+\frac{1}{2} \int_{-\pi}^{\pi}{dx}=\pi$
  由此可见 $k_i^{cos}=\int_{-\pi}^{\pi}{f(x)cos(ix)dx}/\pi$

傅里叶级数

有了前面的知识,我们自然而然的就可以导出傅里叶级数了.我们先来看看傅里叶级数的定义.

如果 $f(x)$是周期 $2\pi$的函数.那么以下展开形式被称作傅里叶级数

$f(x)=\frac{a_0}{2}+\sum_{k=1}^{\infty}(a_kcos(kx)+b_ksin(kx))$

其中, $a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)dx}$
$b_k=\frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)sin(kx)dx}$
$a_k=\frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)cos(kx)dx}$

有了傅里叶级数的定义,我们来看看收敛定理.

设 $f(x)$是周期为 $2\pi$的周期函数,如果它满足:

• 在一个周期内连续或只有有限个第一类间断点.

• 在一个周期内至多只有有限个极值点

则 $f(x)$的傅里叶级数收敛,且

• 当x是 $f(x)$的连续点时,级数收敛于 $f(x)$.

• 当x是 $f(x)$的间断点时,级数收敛于 $\frac{1}{2}[f(x^{-})+f(x^{+})]$

举例

傅里叶级数使用的互相正交的三角函数个数为无线个.也就是说这个三角函数空间为无线维的.但是我们可以在有限维度来观察福利叶级数的行为.我先来看看一个简单的例子比如函数,一个简单的连续函数.这个函数是周期为 $2\pi$的函数,这个函数的在 $[-\pi, \pi]$上面的定义为

$\left\{ \begin{aligned} x+\pi, (-\pi<x\leqslant 0)\\ -x+\pi, (0<x\leqslant \pi) \end{aligned} \right.$

整个函数的图像如下图

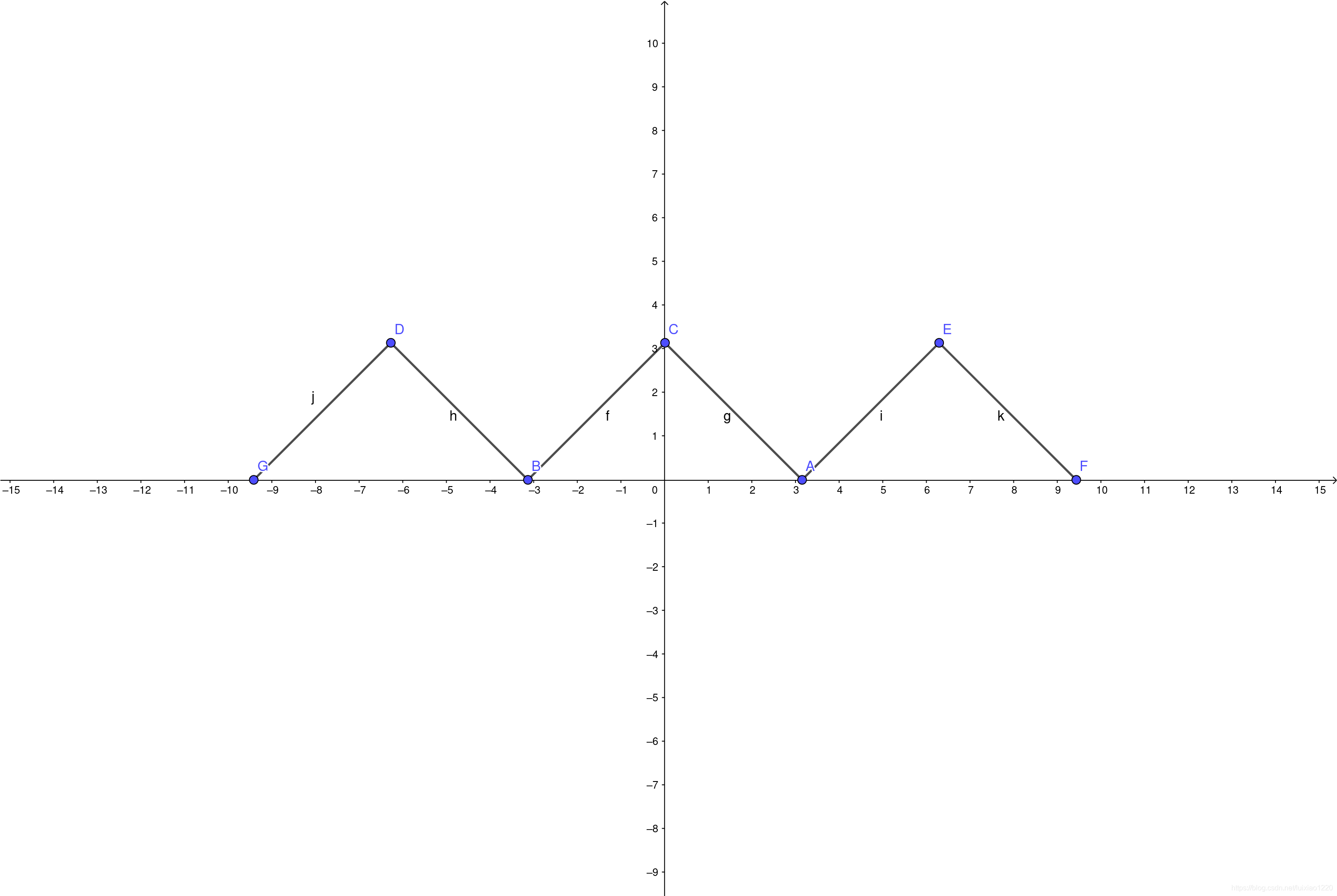
我们这里不使用无线维的三角函数集合.而是使用有限维度的三角函数集合.会发生什么?比如我们使用

$1, cos(x),sin(x)$

按照我们刚开始的方法,也就是正交三角函数的系数求解方法.我们可以展开出这样的的形式

$\frac{4 \cos (x)}{\pi }+\frac{\pi }{2}$
这个函数在 $[-\pi,\pi]$的图象为.这个图象看起来和我们原来的函数图象比较起来,一点儿也不像.但是通过我们以前的分析,可以知道我们的原函数实际上,是含有 $\frac{4 \cos (x)}{\pi }$和 $\frac{\pi }{2}$,成分的.但是因为我们并没有把更为高频的成分加入进来.

这个图形只能说大体上和我们原函数相像而已.接下来我们试着加入更高频的成分.

\newpage
我们现在加入更高频的成分.

$1, cos(x), sin(x), cos(2x), sin(2x), cos(3x),sin(3x)$

我们求得的函数为

$\frac{4 \cos (x)}{\pi }+\frac{4 \cos (3 x)}{9 \pi }+\frac{\pi }{2}$

图象为

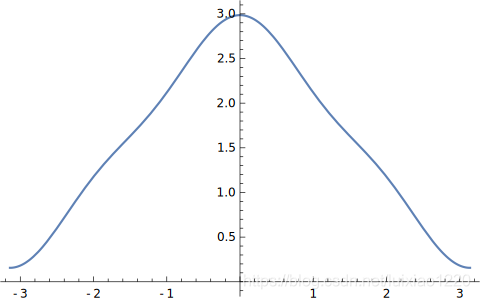
人眼可以看出,这个函数与原函数越来越像了.接下来我们加入更为高频的成分.比如
$1,sin(x),cos(x),\cdots, sin(9x),cos(9x)$

我们求得的函数为
$\frac{4 \cos (x)}{\pi }+\frac{4 \cos (3 x)}{9 \pi }+\frac{4 \cos (5 x)}{25 \pi }+\frac{4 \cos (7 x)}{49 \pi }+\frac{4 \cos (9 x)}{81 \pi }+\frac{\pi }{2}$

图象为

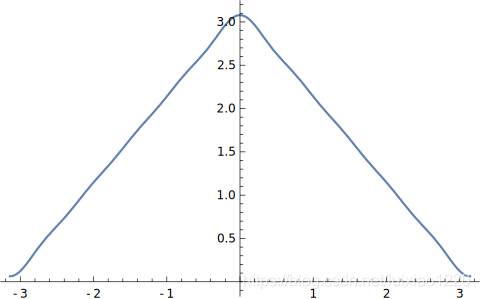
\newpage
这个函数又更为接近原函数了.可见当我们添加更为高频的成分之后,函数越来越贴近原函数了.最后我们加入非常高的高平成分进去.

$1, sin(x), cos(x), \cdots, sin(99x), cos(99x)$

求得的函数我就不列出来了,因为很长很复杂了.但是我们可以把它的图像输出出来.

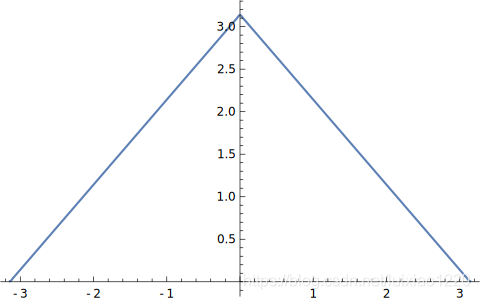
这下你凭借肉眼是看不出来这个函数和原函数的区别的.当我们将频率成分扩展到无限的时候.我们就能够得到一个傅里叶级数展开式组成的函数,它在数学上严格等于原函数.

一般周期傅里叶级数

如果一个函数的周期不是 $2\pi$怎么办?假如一个函数的周期为 $2l$.那么这下该怎么办呢?其实也很容易的.我们可以将 $2l$周期的函数变为 $2\pi$周期.如何做?换元法而已.我们来看看.如何使用换元法将一个周期为 $2l$的函数换成一个周期为 $2\pi$的函数.

$f(x+2l)=f(x)$

只需要进行变换一下自变量就行了. $x=\frac{l}{\pi}z$这样就可以了.然后我们可以换回来,就回到了原来的形式.这样我们可以得到如下的傅里叶系数展开式形式
$\frac{a_0}{2}+\sum_{k=1}(a_kcos(\frac{k\pi}{l}x)+b_ksin(\frac{k\pi}{l}x))$

其中, $a_0=\frac{1}{l}\int_{-l}^{l}{f(x)dx}$
$a_k=\frac{1}{l}\int_{-l}^{l}{f(x)cos(\frac{k\pi}{l}x)dx}$
$b_k=\frac{1}{l}\int_{-l}^{l}{f(x)sin(\frac{k\pi}{l}x)dx}$

复数形式

傅里叶级数的复数形式和上面写出的三角函数形式没有本质区别.他们只是同样的数学概念的不同形式而已.可以互相转换.值得注意的是,我们讨论的 $x$自变量的取值范围属于 $\Bbb{C}$不仅限于 $\Bbb{R}$

下面我们就根据一般形式进行复数形式的推到,我们要用到的根据是欧拉公式

$e^{ix}=cos(x)+sin(x)i$

那么我们可以根据欧拉公式进行转换

$cos(\frac{k\pi}{l}x)=(e^{\frac{k\pi x}{l}i}+e^{-\frac{k\pi x}{l}i})/2$
$sin(\frac{k\pi}{l}x)=-(e^{\frac{k\pi x}{l}i}-e^{-\frac{k\pi x}{l}i})i/2$
将上面的公式带入原来的级数里面我们整理可得.

$\frac{a_0}{2}+\sum_{k=1}^{\infty}\left[ \frac{a_k-ib_k}{2}e^{\frac{k\pi x}{l}i} + \frac{a_k+ib_k}{2}e^{-\frac{k\pi x}{l}i}\right]$

你可以假设 $c_0=\frac{a_0}{2},c_{n}=\frac{a_k-ib_k}{2},c_{-n}=\frac{a_k+ib_k}{2}$,并化简可得
$c_n=\frac{1}{2l}\int_{-l}^{l}{f(x)e^{-\frac{k\pi x}{l}}dx}$
$c_{-n}=\frac{1}{2l}\int_{-l}^{l}{f(x)e^{\frac{k\pi x}{l}}dx}$
由此可见系数的形式可以统一为
$c_n=\frac{1}{2l}\int_{-l}^{l}{f(x)e^{-i \frac{k\pi x}{l}}dx},(k=0, \pm 1, \pm 2, \cdots)$

如此以来,傅里叶级数就可以变为更为简单的形式

$\sum_{-\infty}^{\infty}c_ne^{\frac{k\pi x}{l}i}$

补充

1. 刚才的例子里面并不含sin函数成分.是因为巧合.如果我们的函数更为一般些.图象更为复杂的话.里面一般都会含有sin函数成分.当然这是和函数 $f(x)$的奇偶性有关的.

2. 傅里叶级数的展开式所含有的频率成分是固定的,而且是离散的.他们分别是.

3. 对于有个函数,比如只有一个区域有定义,切满足傅里叶级数的收敛性质的函数.可以做延拓.也就是重复那个区段,就可以把它变成周期函数.然后进行傅里叶级数的变换.

$\frac{1}{2\pi},\frac{1}{\pi},\frac{3}{2\pi},\frac{2}{\pi},\frac{5}{2\pi}, \cdots, \frac{n}{2\pi},\cdots$

傅里叶变换

有了傅里叶级数的基础最好趁热打铁,学习傅里叶变换.傅里叶级数有什么缺点呢?还是有的,比如对于定义在全数域上而没有周期的函数怎么办?接下来我们看看如何从傅里叶级数慢慢的导出傅里叶变换.
$c_n=\frac{1}{2l}\int_{-l}^{l}{f(x)e^{-i \frac{n\pi x}{l}}dx},(n=0, \pm 1, \pm 2, \cdots)$
$\sum_{-\infty}^{\infty}c_ne^{\frac{k\pi x}{l}i}$
对于一般周期的傅里叶级数,变换后的频率成分主要是

$\frac{\pi}{l},\frac{2\pi}{l},\cdots, \frac{k\pi}{l}, \cdots$

对于不同的周期 $l$,频率成分不一样.那么我们来举例看看.根据不同的 $l$来看看不同的傅里叶级数所含有的频率成分.

• $l=1$
  

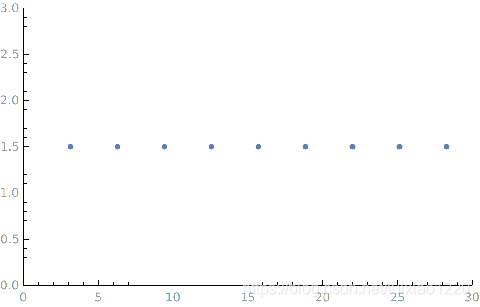
  \newpage

• $l=2$

• $l=5$

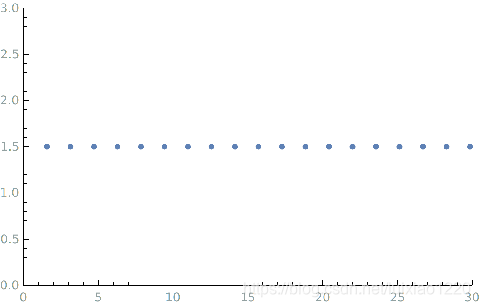
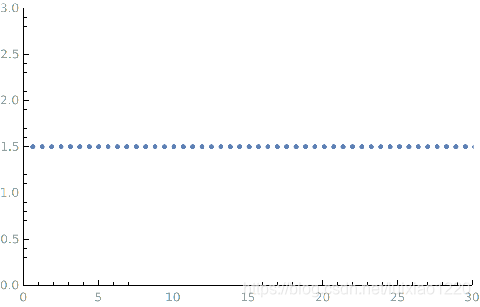
• $l=20$

  

由此可见,当周期趋近于无穷大的时候.傅里叶级数将会包含所有的频率成分.变成一个连续的频率成分.我们看看如何将傅里叶级数变成连续的.
其实也不难,就是取极限.

$f(x)=\lim_{l\rightarrow \infty} \sum_{-\infty}^{\infty} \left[ c_ne^{\frac{k\pi x}{l}i} \right]$ 把 $c_n$也带入进去可得.
$f(x)=\lim_{l=\infty}\sum_{k=-\infty}^{\infty} \left[ (\frac{1}{2l}\int_{-l}^{l}{f(t)e^{-i \frac{k\pi t}{l}}dt}) e^{\frac{k\pi x}{l}i} \right]$ 进行化简

$f(x)=\lim_{l\rightarrow \infty} \sum_{k=-\infty}^{\infty} \left[ \frac{1}{2l}\int_{-l}^{l}{f(t)e^{\frac{(x-t)\pi k}{l}}dt} \right]$

我们现在来看看引入一个变量 $\lambda_k=\frac{k\pi}{l}$.这个正是频率成分. $\Delta\lambda=\lambda_{n+1}-\lambda_n=\frac{\pi}{l}$.我们带入上面的式子.

$f(x)=\lim _{l \rightarrow \infty} \sum_{k=-\infty}^{\infty}\left[\frac{1}{2 \pi} \int_{-l}^{l} f(t) e^{\lambda_{k} i(x-t)} d t\right] \Delta \lambda$

当 $l \rightarrow \infty$.我们可以得
$f(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(t) e^{i \lambda(x-t)} d t d \lambda$
整理一下,我们可以得到下面的式子
$f(x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty}\left(\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} f(t) e^{-i \lambda t} d t\right) e^{i \lambda x} d \lambda$

我们把里面的一个部分
$\hat{f}(\lambda)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}{f(t)e^{-i\lambda t}dt}$
叫做傅里叶变换

我们来比较一下在傅里叶级数中的 $c_n$和傅里叶变换中的 $\hat{f}(\lambda)$

• $c_n=\frac{1}{2l}\int_{-l}^{l}{f(x)e^{-i \frac{n\pi x}{l}}dx},(n=0, \pm 1, \pm 2, \cdots)$

• $\hat{f}(\lambda)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}{f(t)e^{-i\lambda t}dt}$

可见傅里叶级数中的系数在周期无穷大的情况下就会,变成傅里叶变换的形式.傅里叶变换的这个函数值代表的是什么意思?

$\hat{f}(\lambda)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}{f(t)e^{-i\lambda t}dt}$

这个函数是一个以 $\lambda$为自变量的一个函数.这个自变量就是代表的物理意义是频率.而函数求得值是什么呢?它是一个复数.复数怎么来解释?这个需要将复数形式还原为实数的形式.当我们的原函数 $f(x)$是一个定义在实数域上的信号的时候.我们怎么来解释
$\hat{f}(\lambda)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}{f(t)e^{-i\lambda t}dt}$
我们来看看如何重新根据 $\hat{f}(\lambda)$计算振幅和频率成分.

$\hat{f}(\lambda)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}{f(t)e^{-i\lambda t}dt} \mapsto e^{i\lambda x}$
$\hat{f}(-\lambda)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}{f(t)e^{i\lambda t}dt} \mapsto e^{-i\lambda x}$
将后面的项展开可得
$\hat{f}(\lambda)cos(\lambda x)+i\hat{f}(\lambda) sin(\lambda x)$
$\hat{f}(-\lambda)cos(\lambda x)-i\hat{f}(-\lambda) sin(\lambda x)$
合并同类项可得
$(\hat{f}(\lambda)+\hat{f}(-\lambda))cos(\lambda x)+i(\hat{f}(\lambda)-\hat{f}(-\lambda))sin(\lambda x)$
又因为
$\hat{f}(\lambda)+\hat{f}(-\lambda)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}{f(t)cos(\lambda t)dt}$
$\hat{f}(\lambda)-\hat{f}(-\lambda)=-i\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}{f(t)sin(\lambda t)dt}$
所以,我们可以最终得到一个不含虚数的展开式的两相.
$\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}{f(t)cos(\lambda t)dt}cos(\lambda x)+\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}{f(t)sin(\lambda t)dt} sin(\lambda x)$
这就可以复原出两个频率相同的正余弦信号.

傅里叶变换举例

• $f(x)=sin(x)$

  1. 傅里叶变换的结果
     $\hat{f}(\lambda)=-i \sqrt{\frac{\pi }{2}} \delta (\lambda -1)+i \sqrt{\frac{\pi }{2}} \delta (\lambda +1)$

  2. 完整的 $f(x)$形式为
     $f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}{\left[-i \sqrt{\frac{\pi }{2}} \delta (\lambda -1)+i \sqrt{\frac{\pi }{2}} \delta (\lambda +1)\right]e^{i\lambda x}d\lambda}$
     我们化一下简得 $f(x)=\frac{1}{\sqrt{2\pi}} \left[ -i \sqrt{\frac{\pi}{2}}e^{i \cdot 1 \cdot x}+i \sqrt{\frac{\pi}{2}} e^{i\cdot -1 \cdot x} \right]$ 再次化简可得 $f(x)=sin(x)$

  注意所谓的 $\delta(x)$是个什么函数.它的定义其实很简单.他的性质如下 $\delta(x)=0, x\neq 0$时 $\delta(x)=\infty, x=0$.另外 $\int_{-\infty}^{\infty}{\delta(x)f(x)dx}=f(0)$.

• $f(x)=x$

  • 傅里叶变换得
    $\hat{f}(\lambda)=i \sqrt{2 \pi } \delta '(\lambda )$

  • 那么傅里叶逆变换的完整性时为
    $f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}{\hat{f}(x)e^{i\lambda x}d\lambda}$

    积分过程如下

    • $\int_{-\infty}^{\infty} i \delta^{\prime}(\lambda) e^{i \lambda x} d \lambda$

    • $i \left[ \int_{-\infty}^{\infty}{\delta(\lambda)e^{i\lambda x}d\lambda}-ix \int_{-\infty}^{\infty}{\delta(\lambda)e^{i\lambda x}d\lambda} \right]$

    • $i(e^{0}-ixe^{0})=x$

  • 最终结果是 $f(x)=x$