线性代数 or 量子力学 ? (外传：傅里叶级数 与 傅里叶变换学习笔记)

我们在量子力学的道路上已经越走越远了，但是在这一段时间的学习中我发现数学基础的扎实与否对我们进一步学习量子力学的相关知识起到了决定性的作用（似乎理工科都是这样~~），本期我们不再学习量子力学的知识，而是静下心来好好的研究一些数学知识——傅里叶分析，当然了，这对我们后面量子力学的学习至关重要！！

一 . 三角函数系的正交性

在进行推导之前，先给大家打个预防针，傅里叶分析的推导与理解是高数里面较为复杂和繁琐的，且难于理解，不过只要大家抽出有个小时来和我一起算一算，相信小伙伴们会发现，这似乎并没有从前你在学高数的时候感觉 的那么难！千万不要因为博客的内容多，篇幅长就半途而废！
好，下面我们正式开始：

相信大家都记得在前面我们推到 波函数与薛定谔方程 的时候，简单的提到过 函数的正交性，用公式来说就是：
$\int_{a}^{b} f(x)g(x) dx= 0$则称函数 $f(x)$与 $g(x)$在区间 $[a,b]$上正交。（这个是非常简单的，类似于向量改成函数即可，与我们的态矢量和波函数有异曲同工之妙！）

下面，发挥大家类比模仿的能力，我们将这个知识套用在以 $2 \pi$ 为最小周期的三角函数上，我们给它起一个名字就叫 三角函数的正交性。举个例子就是：
$\int_{-\pi}^{\pi} (sinx\cdot cosx )dx = 0$
$\int_{-\pi}^{\pi} cos (x) dx = 0$
（注意一下，在这里，我们不一定非要是2个函数的乘积为 0，一个函数也是可以的，因为在三角函数中 ，二倍角与和差化积公式完全可以做到这一点。。。）
当然了，三角函数有很多，满足以上条件的函数肯定不止我们列举的这两个，所以引入一个三角函数系：
$\left \{ 1, cos x,sinx,cos2x,sin2x ...... cos(nx) ,sin(nx)...\right \}$
其实啊，这一串的 第一项 $1$ 前面还少一个0 ，因为 0 可以写成， $sin(0x)$ ，1也可以写成:
$cos(0x)$ ，所以这样就可以看成：
$\left \{ sin (0x),cos(1x), cos x,sinx,cos2x,sin2x ...... cos(nx) ,sin(nx)...\right \}$
像这种数学理解上的小窍门 ，在同济之类的教科书上你是找不到的，但是，这就是数学的美丽和神秘之处。。。。

好，所谓三角函数系的正交性，其实就是指在三角函数系中任何不同的两个函数的乘积在区间 $[-\pi , \pi ]$上的积分为 0 。我们随手写几个便可验证：
$\int_{-\pi }^{\pi} sin(nx)dx = 0 \left ( n=1,2,3... \right )\\ \int_{-\pi }^{\pi} sin(kx)cos(nx)dx = 0 \left ( k,n=1,2,3... \right )\\ \int_{-\pi }^{\pi} cos(kx)cos(nx)dx = 0 \left ( n=1,2,3... ,k\neq n \right )\\ \int_{-\pi }^{\pi} sin(kx)sin(nx)dx = 0 \left ( n=1,2,3... ,k\neq n \right )$
这里我们就不证明了，但可以提示一下用积化和差的公式转化。

二 . 傅里叶级数的推导

我们先来考虑一个周期函数，假设它的周期为 $2\pi$, 也就是 $f(x) = f(x+2\pi)$,像这样一个函数，我们可以把它展开成一个三角级数，（在这里我们的目的是推导傅里叶级数，所以对我们的假设没有过多的要求，但是，不是所有的周期函数都能展开成傅里叶级数，其需要满足：收敛定理 ，狄利克雷充分条件,忘了的同学翻阅同济七版下册 $p311$），其展开的式子为：
$f(x) = \sum_{n=0}^{\infty }a_{n} cos\;nx + \sum_{n=0}^{\infty }b_{n} sin\;nx$
这时候 ，就有同学说了：怎么和我们教科书上不一样啊，我们教科书的推导的原始式是这样的啊：
$f(x) = \frac{a_{0}}{2} + \sum_{n=1}^{\infty }\left ( a_{n} cos \;nx + b_{n} sin\;nx \right )$
为啥不一样啊，其实，我们用的红色式子是从 $n =0$开始求和，而下面的式子是从 $n =1$开始的，改写一下，我们大胆的猜一下：多出来的 $\frac{a_{0}}{2}$(我们叫它直流分量) 就是红色式子的第0项（目前我还是猜的）到时是不是，我们来算一下便知：
$f(x) = \sum_{n=0}^{\infty }a_{n} cos\;nx + \sum_{n=0}^{\infty }b_{n} sin\;nx \\ =a_{0}cos\;0x +\sum_{n=1}^{\infty }a_{n} cos\;nx +b_{0}sin\;0x + \sum_{n=1}^{\infty }b_{n} sin\;nx\\ =a_{0}+ \sum_{n=1}^{\infty }a_{n} cos\;nx + \sum_{n=1}^{\infty }b_{n} sin\;nx \qquad \qquad \qquad(1 )$

眼尖的小伙伴们又知道了：这你在骗我们啊！！ 这明明是 $a_{0}$，不是 $\frac{a_{0}}{2}$ 啊,别急，且听我慢慢道来:既然问题出现在 $a_{0}$ 处，我们干脆直接求一下 $a_{0}$ 到底是什么不就晓得了。

(1)求 $a_{0}$

我们对蓝色的（1）式结果左右两边在 $[-\pi,\pi]$ 上同时进行积分：
$\int_{-\pi}^{\pi} f(x)dx = \int_{-\pi}^{\pi} a_{0}dx + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty }a_{n} cos\;nx dx + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty }b_{n} sin\;nx dx \qquad \qquad \qquad(2 )$
如下图，简单的积分运算我们应该都是会的，我红圈中的提到积分符号前面去，然后是最重要的是，用 1 去替换红圈，

所以得到的就是这样的：
$a_{n} \int_{-\pi}^{\pi} \sum_{n=1}^{\infty } 1\cdot cos\;nx dx +b_{n} \int_{-\pi}^{\pi} \sum_{n=1}^{\infty } 1\cdot sin\;nx dx$
这时候，我们前面花了大功夫的三角函数的正交性就发挥大用场了，因为 $1=cos\;0x$ ，所以上面这一大串都是0, 是不是感觉特别爽，故而上述(2)式就变成了：
$\int_{-\pi}^{\pi} f(x)dx = \int_{-\pi}^{\pi} a_{0}dx$
用一下牛顿莱布尼茨公式就求出： $a_{0} = \frac{1}{2 \pi} \int_{-\pi}^{\pi}f(x)dx$

此 $\frac{a_{0}}{2}$非彼 $\frac{a_{0}}{2}$，在教材中为了方便，把这个式子中 分母部分的 $2$ 舍去了，所以，我们本次使用的原始式 与 教材中的几乎是一模一样的知识，此 $a_{0}$ 非 教材中的 $a_{0}$，但是本质没有发生变化。

扫描二维码关注公众号，回复： 11216602 查看本文章

(2)求 $a_{n}$

前面的运算中，我们已经把中三个未知中的 $a_{0}$顺利求解出来了，那么剩下的两个是怎么求呢？

这里目前有两个 $a_{n}$， $b_{n}$但是却只有一个式子，理论上是解不出来的，但是我们我们可以设法消掉后面与 $b_{n}$有关的部分，怎么消？能使用三角函数系的正交性吗？ 但是这个式子目前看来，似乎并不满足该条件，没关系，我们可以创造条件:

（1）等式左右两边同乘 $cos\; mx$,再同时在 $[-\pi,\pi]$上积分得：
$\int_{-\pi}^{\pi} f(x)cos\;mxdx = \int_{-\pi}^{\pi}\frac{ a_{0}}{2}cos\;mxdx + a_{n}\int_{-\pi}^{\pi} \sum_{n=1}^{\infty } cos\;nxcos\;mx dx + b_{n} \int_{-\pi}^{\pi} \sum_{n=1}^{\infty } sin\;nxcos\;mx dx$
（2）还是同样的道理，等式右边的第一，三项根据三角函数的正交性直接等于0 消去，得：
$\int_{-\pi}^{\pi} f(x)cos\;mxdx =a_{n}\int_{-\pi}^{\pi} \sum_{n=1}^{\infty } cos\;nxcos\;mx dx$
注意，此时分 $m=n$与 $m\neq n$分别考虑，而当 $m\neq n$时,根据这个: $\int_{-\pi }^{\pi} cos(kx)cos(nx)dx = 0 \left ( n=1,2,3... ,k\neq n \right )$ ，又知其为 0，所以只有当 $m=n$时，才能求解：
$\int_{-\pi}^{\pi} f(x)cos\;nxdx =a_{n}\int_{-\pi}^{\pi} \sum_{n=1}^{\infty } cos^{2}\;nx\ dx= a_{n}\cdot \pi$
所以 $a_{n}$便求出来了 ：
$a_{n} = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x)cos\;nxdx \qquad \qquad (n=1,2,3....)$
,

(3)求 $b_{n}$

和 求 $a_{n}$ 的步骤几乎相同，只是在在第一步不是同乘 $cos\; mx$,而是 $sin\; mx$.在这里就不赘述了，最后得：
$b_{n} = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x)sin\;nxdx \qquad \qquad (n=1,2,3....)$

到这里，我们已经把 $a_{0},a_{n},b_{n}$都解出来了，那么基本上算是完成了本次博客学习的第一步，但是我们这里研究的傅里叶级数的推导是建立在周期为 $2\pi$上的，那么如果这时候周期是 $2l,l$不是 $\pi$呢？又该怎么办？除此之外，这个三角级数与复数之间有非常密切的关系，形成的欧拉公式 $e^{i\theta } = cos \theta +i sin\theta$与之又有何渊源呢？

再三强调，小伙伴们一定要自己去推导，去感受其中的细微末节，在数学的学习中：细微之处，方显功夫啊！！！

三 ，拓展及其复数表达形式

<1> 周期拓展

在这里，我们尝试将一个周期为 $2 l$（ $l$为不是 $\pi$的任意值）的三角函数展开为傅里叶级数，其实原理很简单，换元即可：
函数 $f(t) =f(t+2l)$ ,将 $t$ 换成 $t = \frac{l}{\pi}x$, 进而设一个 $g(x)$为 $f(t) = f(\frac{l}{\pi}x) =g(x)$,同样的， $g(x)= g(x+2\pi)$,通过这个简单的换元. 我们就可以将 周期为 $2 l$的函数 $f(t)$ 转化为 周期为 $2 \pi$的函数 $g(x)$.

那关于 $g(x)$如何展开成傅里叶级数呢？这个并不难：

$g(x) = \frac{a_{0}}{2} + \sum_{n=1}^{\infty }\left ( a_{n} cos \;nx + b_{n} sin\;nx \right )\\a_{0} = \frac{1}{2 \pi} \int_{-\pi}^{\pi}f(x)dx\\a_{n} = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x)cos\;nxdx \qquad \qquad (n=1,2,3....)\\b_{n} = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x)sin\;nxdx \qquad \qquad (n=1,2,3....)$	$f(t) = \frac{a_{0}}{2} + \sum_{n=1}^{\infty }\left ( a_{n} cos \;\frac{n\pi}{l}t + b_{n} sin\;\frac{n\pi}{l}t \right)\\a_{0} = \frac{1}{l} \int_{-l}^{l}f(t)dt\\a_{n} = \frac{1}{l} \int_{-l}^{l}f(t)cos\;\frac{n\pi}{l}t \;dt \qquad \qquad (n=1,2,3....)\\b_{n} = \frac{1}{l} \int_{-l}^{l}f(t)sin\;\frac{n\pi}{l}t \;dt \qquad \qquad (n=1,2,3....)$
左边是 $[-\pi,\pi]$上周期为 $2\pi$我们前面求的傅里叶级数	右边是换元替换后任意周期 $2l$的傅里叶级数

很明显，我们欲得到右式，只需将左边中所有的 $x$ 换成 $\frac{\pi}{l}t$即可，至此，其他周期的傅里叶级数也基本上得到解决，那有小伙伴就会问了：如果这个周期 $T$ 无限大，趋近于无穷的时候，又当如何？
这个与我们后面要说的傅里叶变换有关，现在这埋个伏笔！！

<2> 复数的表达形式

想要学习傅里叶变换，就必须先要了解了解傅里叶级数的复数表达式，，而想要了解傅里叶级数的复数表达式，就必须先了解宇宙中最 $beautiful$ 的公式—— 欧拉公式：
$e^{i\theta } = cos \theta +i sin\theta$
其中： $cos \theta = \frac{1}{2}(e^{i\theta } + e^{-i\theta } )\\ sin \theta = -\frac{1}{2}(e^{i\theta } - e^{-i\theta } )$
这里我们改一下推导前的原始式:
$f(t) = \frac{a_{0}}{2} + \sum_{n=1}^{\infty }\left ( a_{n} cos \;n\omega t + b_{n} sin\;n\omega t \right )$
将上面面紫色的式字带入，下面高能预警：

我们把橘色框中的改一下得到(把 $n$ 改成 $-n$ )：
$\sum_{n= -\infty }^{ -1} \frac{a_{-n}+ib_{-n}}{2} e^{in\omega t}$
同时，我们还需要将第一项 $\frac{a_{0}}{2}$改成：
$\sum_{n=0}^{0} \frac{a_{0}}{2} e^{in\omega t}$
我们想通过这两步将上述结果的三项式子用写成一个更一般的公式，用一个式子来表示。故而推导的完整过程为：

其中的 $C_{n }为$（CSDN的公式排版真的巨烂。。。。大家将就着看）：
$C_{n } = \left\{ \begin{aligned} \frac{a_{0}}{2}\qquad \qquad n=0 \\ \frac{a_{n}-ib_{n}}{2}\qquad \qquad n=1,2.3...\\ \frac{a_{-n}+ib_{-n}}{2}\qquad \qquad n=-1,-2.-3... \end{aligned} \right.$
好，这个时候，我们再把前面已经算好的：
$a_{0} = \frac{2}{T} \int_{0}^{T}f(t)\;dt \qquad \\ a_{n} = \frac{2}{T} \int_{0}^{T} f(t)cos\;n\omega t\;dt \qquad \qquad (n=1,2,3....)\\ b_{n} = \frac{2}{T} \int_{0}^{T} f(T)sin\;n\omega t\;dt \qquad \qquad (n=1,2,3....)$

分别代入蓝色 $C_{n }$的各项，就能得到
$C_{n } = \left\{ \begin{aligned} \frac{1}{T} \int_{0}^{T}f(t)dt \qquad \qquad n=0 \\ \frac{1}{T} \int_{0}^{T}f(t) e^{-in\omega t}dt \qquad n=1,2.3...\\ \frac{1}{T} \int_{0}^{T}f(t) e^{-in\omega t}dt \qquad n=-1,-2.-3... \end{aligned} \right.$
如果你认真算了的话，你会在算的时候就发现，当 $n=1,2,3...$与 $n=-1,-2,-3....$时， $C_{n }$ 竟然是一模一样的！！！你现在是不是很兴奋？那如果我把 $n=0$也包含进来，我估计你会更兴奋！

当 $n=0$的时候：
$\frac{1}{T} \int_{0}^{T}f(t)dt = \frac{1}{T} \int_{0}^{T}f(t)e^{0}dt$

OMG！盖了帽了 ，我的老北鼻，牛逼 $plus$!
这样的话 我们就能得到，一个周期为T的函数， $f(t)=f(t+T)$展开为傅里叶级数，它的复数表达形式就是：

$f(t) = \sum_{-\infty }^{\infty}C_{n}e^{inwt} \qquad C_{n} = \frac{1}{T}f(t)e^{-in\omega t}\;dt$

至此，傅里叶级数的数学推导和介绍算是结束了，下面我们来看一看傅里叶变换！

四 . 傅里叶变换

经过前面我们呕心沥血的推导，我们终于得到了：如果有一个周期函数 $f_{T} (t)=f(t+T)$，（在这里我们用一个下标 $T$表示它是一个周期函数),那么这个周期函数展开为傅里叶级数的复数表达形式为：
$f(t) = \sum_{-\infty }^{\infty}C_{n}e^{inwt} \qquad\qquad (1)\\C_{n} = \frac{1}{T}f(t)e^{-in\omega t}\;dt\qquad\qquad(2)$
其中， $\omega _{o} = \frac{2\pi}{T}$ 称为基频率，但是上述表达式知只是一个同式，真正能区分他们为不同函数的还是这个 $C_{n}$

我们画一个这样的简单示意图，又因为 $C_{n}= a+bi$(因为 $C_{n}$是复数），我们也可以简单画一下（大家请先忽略我这拙劣对的画技(✪ω✪)）。

通过上述的遍历累加公式我们知道,欲得到上上个图中的 $f(t)$函数，我们需要这样即可：
$...C_{-1}e^{-i\omega t}+C_{1}e^{1i\omega t}+C_{2}e^{2i\omega t}+...$
因此，上面这个图就是上上面的 $f(t)-t$函数图在 $n\omega _{0}$为横坐标时的一个在复平面的一个表达形式，由于第一个图是以时间为横坐标的，那么我们把叫做“时域”表达，而第二个图显示了在不同频率下系数的值，我们叫它为其“频率”表达。
关于这个的理解我们等一会再举一个好例子。

前面我们一个说的是周期有限的情况下函数的傅里叶级数，下面我们来说一说当周期趋于无穷大，即周期不存在时，到底是什么情况？

把我们的目光再锁定在频谱图上，两个频率之间的距离我们把它定义成 $\Delta \omega$:
$\Delta \omega = (n+1)\omega_{0} - n\omega_{0}=\frac{2\pi}{T}$
这个时候，如果 $T$无限变大，那么 $\Delta \omega$会变得无限小，到最后，两个频率之间的距离会变得无限小，最终，他们会连在一起。所以，所有离散的这些都会变成连续的，这样他们在三维空间中变成为一条曲线，之后 ，我们可以将横坐标的 $n\omega _{0}$ 改成 $\omega$.

将我们傅里叶变换一开始的（2）式代入到（1）式中，在这里还有一个小技巧， $\frac{1}{T} = \frac{\Delta \omega }{2x}$，替换后我们会得到：
$f_{T}(t) = \sum_{n=-\infty }^{\infty } \frac{\Delta \omega }{2\pi} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} f_{T}(t) e^{-in\omega t} dt e^{in\omega t}\qquad\qquad(3)$
当 $T$ 趋向于无穷（ $T\rightarrow \infty$）的时候，我们来一项一项的分析这个式子：
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} dt \rightarrow \int_{-\infty }^{\infty } dt \qquad\qquad(4)\\ n\omega _{0 }\rightarrow \omega\qquad\qquad(5) \\ \sum_{n=-\infty }^{\infty }\Delta \omega \rightarrow\int_{-\infty }^{\infty }dw\qquad\qquad(6)$
将上面我们得到的（4）（5）（6）式分别代入（3）式得：

其中，橘色框住的部分我们定义为傅里叶变换（FT）：
$F(\omega ) = \int_{-\infty }^{+\infty } f(t)e^{-i\omega t}dt$
而原来的：
$f(t)= \frac{1}{2\pi}\int_{-\infty }^{+\infty } F(\omega ) e^{i\omega t}dw$
就叫做傅里叶变换的逆变换。至此，我们傅里叶分析学习的纯数学推导部分就算是完成了！

五 . 数学的乐趣你想像不到

我们费了九牛二虎之力得到的傅里叶分析到底是用来干啥的呢？其实它的应用非常的广泛，下面，我会以一个例子带你了解傅里叶的天才智慧。。。。
我们先得到一个函数： $\cos x+0.1\cos10x+0.1\cos100x$
我们绘出的图为：

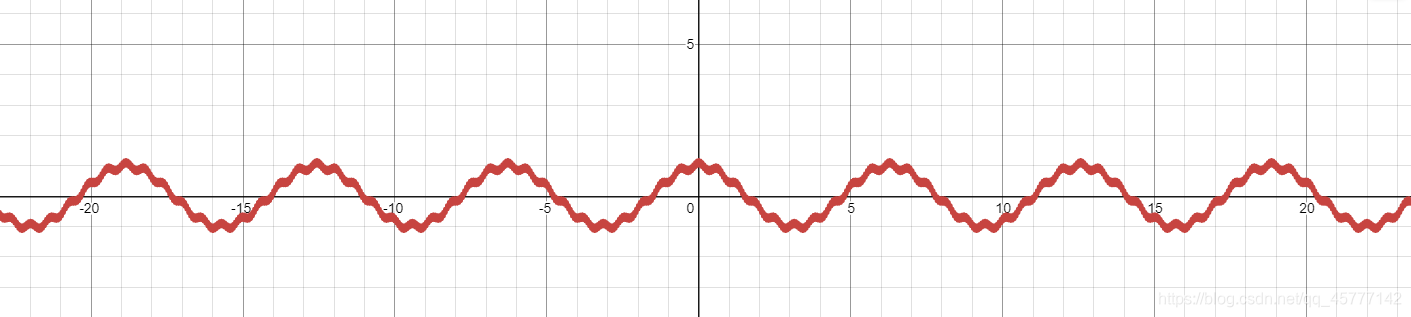
我们可以看到这个图形并不是十分的光滑，其大致的曲线轨迹是 $cos\;x$,我们可以断定 $0.1\cos10x+0.1\cos100x$其实就是 $cos\;x$的噪音，有可能有的同学说，不影响啊，大致差不多，但是我们放大后仔细看一下：

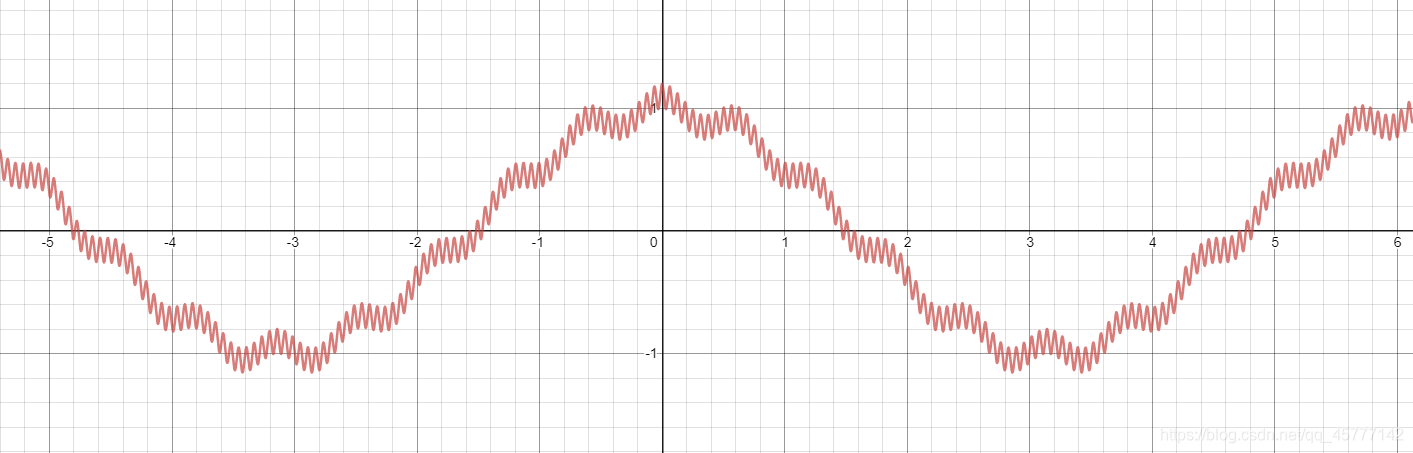
现在，我相信大家可以知道，这个影响是不可忽略的了吧！那么我们怎么样才能滤波，去除高频信号达到降噪呢？
我们一般的滤波器 在低频中滤掉高频的最简单的手段就是积分：将原式积分得：
$\sin x+0.01\sin10x+0.001\sin100x$
这个时候，我们再绘制这个积分函数的图，并将两者进行比较：

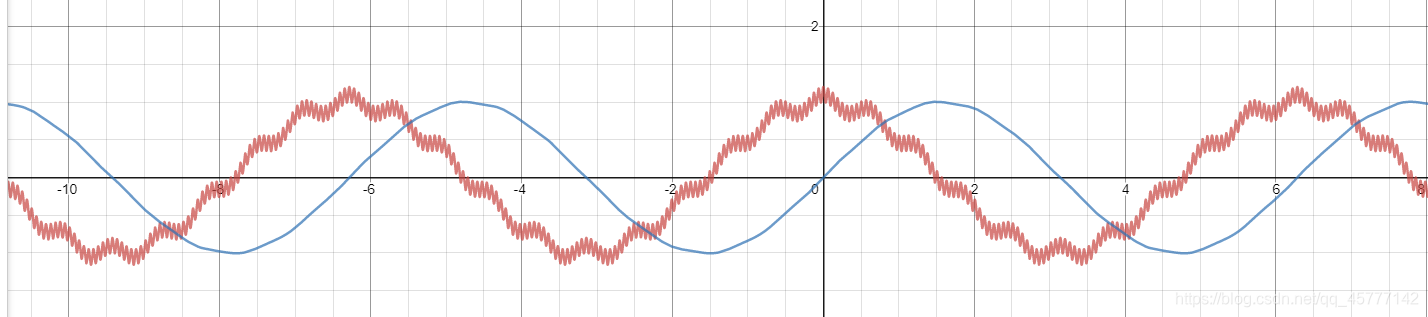
那么，通过这个图，我们可以很清晰的看到蓝色的积分曲线平滑多了，二者只是存在一个相位的差别，降噪效果是非常明显的！
当然，我们必须要承认的是，这个蓝线的轨迹在走的时候并不是那么的完美顺畅，我们可以在对其进行二次积分：
$-\cos x-0.01\cos10x-0.00001\cos100x$

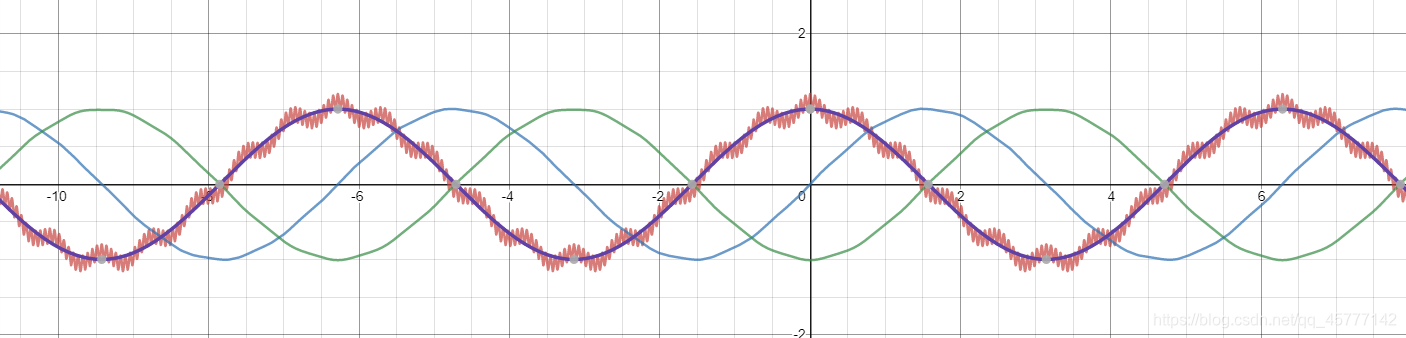
图中绿色的线就是我们二次积分后的曲线，而紫色的曲线（高频粗线中包含的细线）就是我们一直想复原的 $cos\;x$,这一回，我们可以清晰的看出，绿线和紫色的线基本上已经一样平滑的！
这便是傅里叶级数的一个简单但是重要的应用！！