傅里叶分析
傅里叶分析研究如何将一个函数或信号表达为基本波形的叠加。主要研究分支包括傅里叶级数和傅里叶变换。
参考:傅里叶分析之掐死教程(完整版)更新于2014.06.06
频域、时域 与 正弦波
频域类比音符,时域类比乐曲,音符是静止永恒的,乐曲是时间相关的且基于音符的。
频域:

时域:
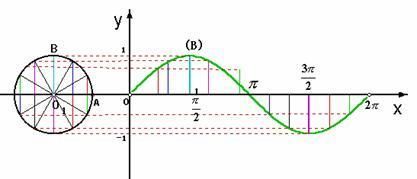
正弦波:正弦波就是一个做圆周运动的质点的历史轨迹平铺在时间轴上,对质点运动照相,得到该质点该时刻的 "相",就是相位,描述质点圆周运动时某一时刻的位置。
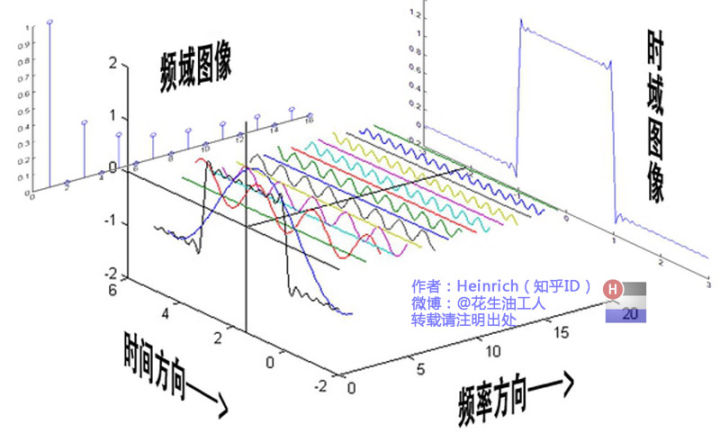
傅里叶级数、时域频域
傅里叶级数把类似波的函数表示成简单正弦波,定义是:将周期函数或周期信号分解成简单振荡函数的集合,即正弦函数和余弦函数。
\[ \begin{aligned} f(t) &=\frac{a_{0}}{2}+a_{1} \cos (\omega t)+b_{1} \sin (\omega t) \\ &+a_{2} \cos (2 \omega t)+b_{2} \sin (2 \omega t) \\ &+\ldots \\ &=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos (n \omega t)+b_{n} \sin (n \omega t)\right] \end{aligned} \]
其中
\[ \begin{aligned} a_{n} &=\frac{2}{T} \int_{t_{0}}^{t_{0}+T} f(t) \cos (n \omega t) d t \\ b_{n} &=\frac{2}{T} \int_{t_{0}}^{t_{0}+T} f(t) \sin (n \omega t) d t \end{aligned} \]
傅里叶级数的图像为
傅里叶变换、时域 与 频域
傅里叶级数将一个时域上的波形转换为多个正弦波叠加,多个正弦波在频域上的表示是离散的;傅里叶变换则将时域上的波形转为频域上的连续图像。
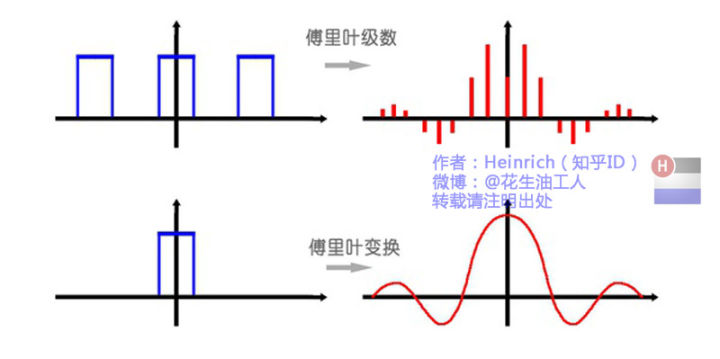
原来频域上离散谱的叠加是求和,现在连续谱就是求积分。
时域转换至频域:
\[ \hat{f}(\xi)=\int_{-\infty}^{\infty} f(x) e^{-2 \pi i x \xi} dx\quad \xi为任意实数 \]
自变量 \(x\) 表示时间 ( 以秒为单位 ),变换变量 \(\xi\) 表示频率 ( 以 Hz 为单位)。频域至时域:
\[ f(x)=\int_{-\infty}^{\infty} \hat{f}(\xi) e^{2 \pi i \xi x} d \xi \]
傅里叶变换的图像为
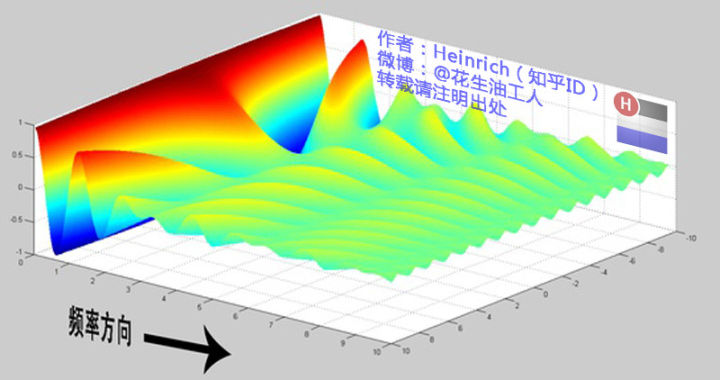
虚数 \(i\)、欧拉公式 与 指数
参考:复数的物理意义是什么? - Heinrich的回答 - 知乎
复数 \(i\) 的物理意义是旋转,函数 \(e^x\) 图像是
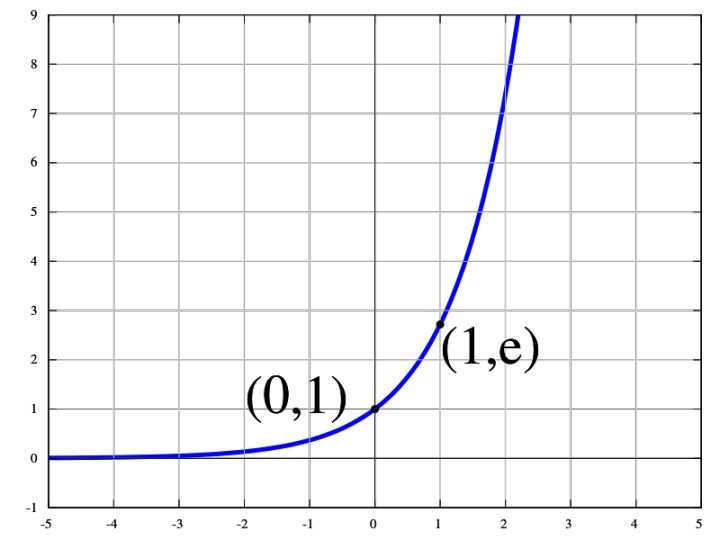
指数加上 \(i\),变成
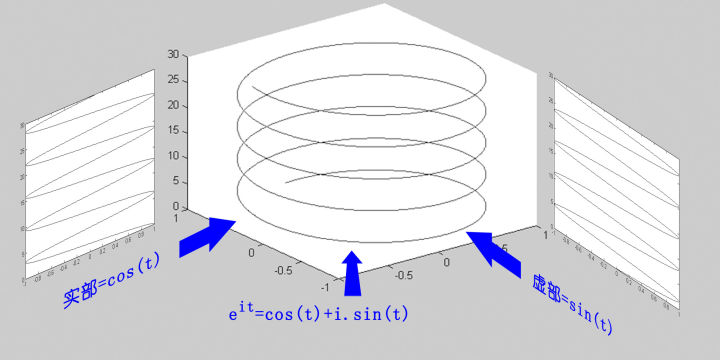
欧拉公式描述一个在复平面上做圆周运动的点,在时间轴上运动轨迹成螺旋线,只看实部,是基础余弦函数,只看虚部,是基础正弦函数(几何形式理解)。
\[ e^{it}=cos(t)+isin(t) \]
当 \(t=\pi\),\(e^{\pi i}=cos(\pi)=-1\),得欧拉公式:
\[ e^{\pi i}+1=0 \]
欧拉公式实现了正弦波与复指数的统一。在欧拉公式的支持下,正弦波的叠加可理解为螺旋形的叠加在实数空间的投影。
欧拉公式另一种代数形式理解,由泰勒公式展开:
\[ \begin{aligned} e^x=1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+...\end{aligned} \]
\[ sin\theta=x-\frac{1}{3!}x^3+\frac{1}{5}x^5+... \]
\[ cos\theta=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4+... \]
当 \(x=i\theta\)
\[ \begin{aligned} e^{i\theta}&=1+i\theta+\frac{1}{2!}(i\theta)^2+\frac{1}{3!}(i\theta)^3+...\\&=1+i\theta-\frac{1}{2!}\theta^2-\frac{1}{3!}i\theta^3+\frac{1}{4!}\theta^4+\frac{1}{5!}i\theta^5+...\\&=(1-\frac{1}{2!}\theta^2+\frac{1}{4!}\theta^4+...)+i(\theta-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5+...)\\&=cos(\theta)+isin(\theta) \end{aligned} \]
所以有
\[ \cos (t)=\frac{e^{i t}+e^{-i t}}{2} \]
在几何意义上理解这个式子就是 \(e^{it}\) 为逆时针旋转的螺旋形,\(e^{-it}\) 为顺时针旋转的螺旋线,\(cos(t)\) 是 这两条旋转方向不同的螺旋线叠加的一半,因为这两条螺旋线的虚数部分相互抵消掉了!
那么傅里叶变换的螺旋线表示为
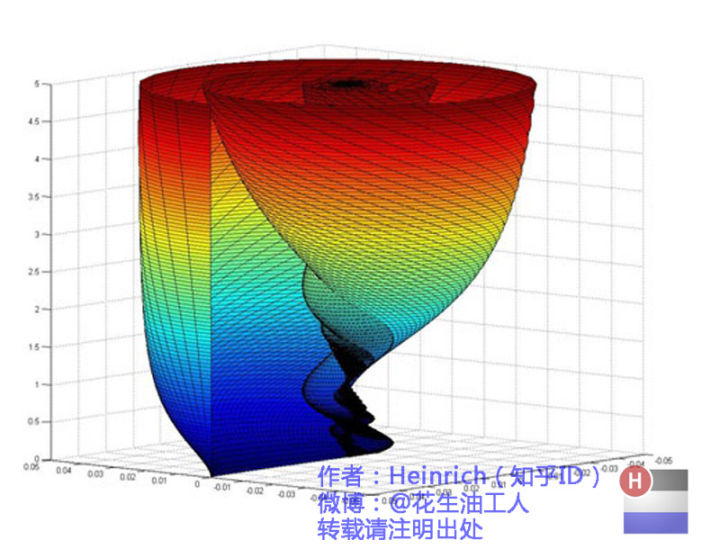
总结
将复频域的螺旋形图投影至实数空间就得频域的波浪图,将频域的波浪图通过傅里叶变换得到最初的时域信号。