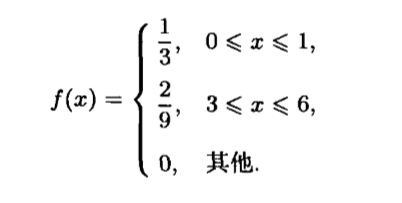【概率论与数理统计 Probability and Statistics 4】—— 随机变量与分布函数

一、随机变量的概念

在引入随机变量之前，比如我们前几篇 $Blog$ 里面讨论的例子都是一些具体化的题目，例如：抛硬币（正面、反面）；抽球（红球、白球、黑球）、、、但是，我们在数学中希望能够把这个实例抽象化，用一个数学的形式描述。因此，我们就引入了随机变量的概念。

在以后，我们把每一个具体化例子里面的样本点 $ω$ 用一个数来表示，而不是用语言文字描述。就如同函数那样，每一个样本点 $ω$ 都可以映射成一个实值 X，所以我们规定一种映射： $X(ω) = X$，这样，我们就可以把原本具体的事件用一些实数表示。 $X$ 就称为随机变量（一般是大写的）

我们可以用： $\{ω|X(ω) = a\}$ 这个意思随机变量 X 取某一特定的数 a 的情况，我们也叫做一个 “事件”，不过一般为了简便起见，我们都是用： $\{X=a\}$ 来表示一个事件

那么： $P\{X=a\}$ 就表示这个事件发生的概率。

1.1 离散型随机变量及其概率分布

什么是离散型随机变量呢？我们举几个例子：（下面的例子都是已经将具体的事件用随机变量表示）

【1】扔骰子：X = 1、2、3、4、5、6，每一个事件发生的概率都是 $\frac{1}{6}$
【2】仍硬币：X = 1、0，每一个事情发生的概率是 $\frac{1}{2}$

我们是这么定义离散型随机变量的： $X = x_k\space(k = 1,2,3,\cdots)$， $x_k$ 必须是可列个。

这里有几点重要说明：

1. 我们以后用大写的 $X$ 表示变量，用小写的 $x$ 表示这个变量可以取的值
2. 根据上面的定义，我们发现：随机变量 $X$ 的取值可以是无限多个，但是必须能够排成一排的，比如说，等比级数。
3. 我们定义： $P\{X = x_k\} = p_k$ ，这里小写的 $p$ 代表具体某一个事件的概率。并且，有： $p_k ≥ 0$、 $\sum p_k = 1$

对于离散型随机变量，我们经常喜欢列概率分布表：如下所示（以投骰子为例）：

X	1	2	3	4	5	6
P	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$

当然也是可以画出分布图的，就是一根一根的线罢了。

关于上面说过的，如果随机变量的取值是无限的情况是怎么样的呢？我们看看一个例子：

X	2	4	8	16	32	$\cdots$
P	$\frac{1}{2}$	$\frac{1}{4}$	$\frac{1}{8}$	$\frac{1}{16}$	$\frac{1}{32}$	$\cdots$

这里所自变量取值的概率的加和是1，是一个等比级数

注意：我们验证离散型随机变量概率分布表是否正确时，可以把求的所有概率加一下，看看是不是等于1，不等于1那肯定错了。

1.2 连续型随机变量及其概率密度函数

我们先来看看概率密度曲线的意义：

红色的曲线就是x的概率密度函数pdf曲线。如果我现在这样问你：P(x = 10) = ?
乍一看，x = 10对应曲线的纵坐标在0.16附近，我们能说x = 10的概率是0.16吗？？

答案是：NO！,P(x=10) = 0!
正如我们在生活中所说的当x=10，我们一般会把10.01，10.001，9.99等等这样的数都当作10，我们以x为某地的降雨量为例，你能保证当天降雨的总量刚刚好在10mm，一滴不多一滴不少吗？

我们上面所讨论的问题，都基于一个前提：就是我们的自变量X是一个连续随机变量，在连续随机变量的概率密度曲线中，X准确等于任何一个数的概率都是0！

那么要怎么表示概率呢？我们可以用一个区间，比如说x在[9.9, 10.1]区间的概率是多少。这样就会取得一个确定的概率P. 在微积分的知识里我们知道，在pdf曲线中计算x落在区间[9.9, 10.1]上的概率就应该是曲线在[9.9, 10.1]那段的面积： $\int_{9.9}^{10.1}f(x)dx$

近似可以看作上图的蓝色矩形的面积。
因此，概率密度曲线中某一x范围 $[x, x+△x]$概率，就是曲线在 $[x, x+△x]$这一范围下与横轴围成的区域的面积

二、分布函数

我们先给出分布函数的定义： $F(x) = P\{X ≤ x\}$
它表示的是随机变量 $X$ 的取值小于 $x$ 的概率，其中 $x∈(-∞,+∞)$，因为 $F$ 也是概率，所以显然有： $F(x) ∈[0,1]$

2.1 分布函数的性质

【性质一】： $0≤F(x) ≤1$
【性质二】： $F(x)$ 函数是一个不减函数，也就是说， $F(x)$ 可以递增，也可以不变，但是不会递减
【性质三】： $F(x)$ 一定是右连续的，其中对于离散型随机变量而言，它一定是右连续；但是对于连续型随机变量而言，它既是右连续又是左连续）

【性质四】： $F(+∞) = \lim_{x\to +∞}F(x) = 1$，这是必然的，因为使得 $X$ 小于等于 +∞就是一个必然事件；同样， $F(-∞) = \lim_{x\to -∞}F(x) = 0$，这也是必然的，因为使得 $X$ 小于等于 -∞ 就是一个不可能事件，概率是0

【性质五】：下面给出的是几个运算性质，但是其实大家知道意思了，就可以自己推导出所有的。
（1） $P\{X≤a\} = F(a)$，这个没啥问题，就是定义。
（2） $P\{X>a\} = 1-F(a)$，因为 $\{x>a\}$ 是 $\{x≤a\}$ 的补集，所以概率就是用1 减
（3） $P\{a<X≤b\} = F(b) - F(a)$，这些关系我们用高中求不等式问题的图特别好理解，如下：

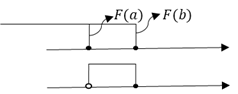
（4） $P\{X=a\} = F(a)-F(a-0)$，这里的 $F(a-0)$ 是啥意思呢？就是左逼近，我们从 $-∞$的地方无限逼近 a 这个点，但是不会等于它。那么也就是说： $F(a-0) = P\{x<a\}$ 。

（5） $P\{a≤X≤b\} = F(b) - F(a-0)$ 同样，咱们自己在脑子里画一下那个区间关系图一下子就出来了

（6） $P\{x<a\}$ 等于啥呢？刚刚其实我们都已经推出来了： $F(a-0) = P\{X≤a\}-P\{X=a\}$

（7） $P\{X≥a\} = 1-P\{x<a\} = 1-F(a-0)$

注意：以上对分布函数的讨论对于离散型随机变量和连续型随机变量均成立！！只有在离散型随机变量中需要考虑端点值，而对于连续型随机变量我们就不管端点值了，因为是连续的！

2.2 离散型随机变量的分布函数

一般的题目通常会有两种：

1. 给出不同 X 取值的概率分布表，让你求分布函数 $F(x)$
2. 给出 $F(x)$，然后反推出概率分布表

第一种情况很简单，不再赘述；对于第二种类型， $F(x)$ 取值的间断点处，就是对应的 $X$ 的取值 ，那么每一个 $X$ 对应的概率就等于 $P\{X=x_k\} = F(x_k)-F(x_k-0)$

我们举一个例子：

我们来看看：很明显，函数 $F(x)$ 的间断点就是 X 的取值，所以我们一眼看出，X 的取值是：-1、1、3.

接下来，我们分别计算 $P(-1), P(1), P(3)$；
$P(-1) = F(-1) - F(-1-0)$，也就是说，是用 $F(-1)$ 的值减去函数从 $-∞$ 逼近 -1的值，我们看到： $F(-1-0) = 0$，所以 $P(-1) = F(-1) - F(-1-0) = 0.5-0 = 0.5$

$P(1) = F(1) - F(1-0) = 0.8-0.5 = 0.3$

$P(3) = F(3) - F(3-0) = 1-0.8=0.2$

那么，就可以列出概率分布表：

X	-1	1	3
P	0.5	0.3	0.2

2.3 连续型随机变量的分布函数

下面的公式需要记忆： $F(x) = \int_{-∞}^xf(t)dt$

还记得吗，在离散型随机变量的分布函数中，我们是通过离散的那些随机变量 X 的概率 P 直接来计算的。而这里，我们的 $f(t)$ 就是连续型随机变量 X 的概率密度分布函数。题目给出概率密度函数，我们需要会计算分布函数 $F(x)$

不过在计算时有陷阱，我们给出的概率密度函数是分段的，自然我们求的 $F(x)$ 也是分段的，那么既然分布函数是分段的，那么积分的时候就要特别注意分段积分（不过分段积分的时候我们也不需要太关系区间端点的问题，因为连续型随机变量的分布函数是连续的，端点取值对结果无影响）

光说无据，我们举个例子：

下面的 function 是一个概率密度函数，求分布函数

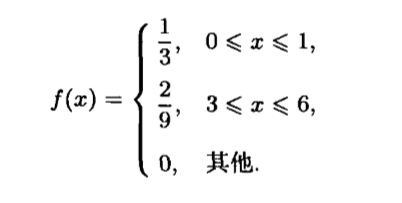
因为分布函数 $F(x)$ 里面的 x 的取值范围是 $(-∞, +∞)$，所以我们需要对整个实数域讨论：

分成下面几个区间：1. $x<0$ $\quad$ 2. $0≤x≤1$ $\quad$ 3. $1<x<3$ $\quad$ 4. $3≤x≤6$ $\quad$ 5. $6<x$

这样区间就囊括了实数域。下面分别计算：

1. $x<0$ 时， $F(x) = \int_{-∞}^xf(t)dt = 0$
2. $0≤x≤1$时， $F(x) = \int_{-∞}^0f(t)dt +\int_{0}^xf(t)dt = 0+\frac{1}{3}x$
3. $1<x<3$时， $F(x) = \int_{-∞}^0f(t)dt +\int_{0}^1f(t)dt + \int_1^xf(t)dt = \frac{1}{3}$
4. $3≤x≤6$时， $F(x) = \int_{-∞}^0f(t)dt +\int_{0}^1f(t)dt + \int_1^3f(t)dt + \int_3^xf(t)dt =\frac{2}{9}x-\frac{1}{3}$
5. 类似地， $6<x$时， $F(t) = \int_{-∞}^0 +\int_0^1+\int_1^3+\int_3^6+\int_6^x =1$

这就是分段积分的意思

另外，对分布函数求导就可以得到概率密度函数。 $F'(x) = f(x)$（注意区间）

OK，本次笔记先记到这，下一篇 $Blog$ 将会具体探讨各种分布！