这是《概率论与数理统计》网上授课的第一次笔记,记录一下这门课基本的几个概念。概率论是相当重要的一门课,在许多领域,例如深度学习,机器学习,数据挖掘等都广泛地运用了概率论的知识
一、基本概念(基础)
【1】 :随机试验必须要满足下面三个条件:
- 在相同的条件下可以重复进行;
- 试验的结果的可能情况不止一种;
- 试验的结果是未知的
【2】 :在随机试验中每一种可能的结果就是随机事件,用大写的 表示
【3】 :在随机试验的重复实施中呈现出来的不变的性质
【4】 :相对于自己的随机实验目的而言,不能再分的事件称为基本事件。这句话怎么理解呢?比如说:我们以投骰子为例,如果我们是要统计骰子投出来的点数,那么,事件 = {点数为 } 就是一个基本事件。但是,如果我们的目的是要统计骰子的落点位置,那么这个时候我们就不再关心骰子的点数,而事件 = {骰子落在 点}就变成了新的基本事件了。
也就是说:试验的目的决定了以什么作为基本事件!
【5】 :这个就很好理解了,由基本事件组合而成的就是复合事件。还是以目的为统计骰子点数的随机试验为例,那么事件 = {点数是偶数} 就是一个复合事件,因为 可以拆成 {点数为2} ∪ {点数为4} ∪ {点数为6}
【6】 :所有基本事件的集合,用 表示。换句话说: 也可以看作是全集,因此试验的结果一定在 里面,也就是说 一定发生。
【7】 :样本空间 里面的元素,用 表示,且
二、事件之间的基本关系
(1)若事件
发生,则事件
必然发生,那么我就有:
(
包含
)
这很好理解,还是以目的为统计骰子点数的随机试验为例,如果事件
= {点数为2} 发生了,那么必然地,事件
= {点数是偶数} 也肯定就发生了。我们也发现,事件
里面就包含了事件
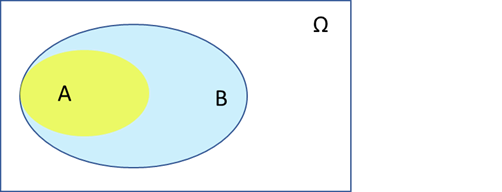
(2)若事件 发生,则事件 必然发生;反过来,若事件 发生,则事件 必然发生,那么我们就说:
(3)若事件 , 不能同时发生,但是也可以同时不发生。也就是说,事件 里面没有包含相同的情况,而且 的所有情况也只是样本空间的一部分。那么,我们就表示为: ,我们称此时 为互斥事件
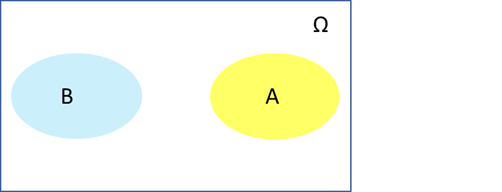
(4)若 不能同时发生,而且只能发生 的其中一个,那么,就意味着事件 里面没有包含相同的情况,而且, 所包含的所有情况就是样本空间。此时,我们说: ;或者 。即 为对立事件。同时,还有: ;

(5)对于上面的(3)情况互斥事件可以做一个推广:如果事件 中任意两个事件都是对立事件,那么
三、事件之间的运算
【1】事件的和:先以两个事件为例,事件 的和,就是事件 中至少有一个事件会发生,这就用 表示。举个例子:比如说投骰子,事件 = {点数为2,4};事件 = {点数为4,6},那么 = {点数为偶数}
特别地,如果 互斥,那么
推广到 n 个事件:
,那么用:
表示事件
至少会发生一个。
同样地,如果
两两互斥,那么
:如果 两两互斥,且 ,那么, 称为互斥完备群
【2】事件的积:如果事件 同时发生,那么我们就说 是事件的积。再举例子:如果事件 = {点数为2,4},事件 = {点数为4,6},那么 = {点数为4}
推广到 n 个事件,我们用:
表示
同时发生。
【3】事件的差:事件 发生,但是事件 不发生,那么我们用 来表示。
辨析题:三个事件 A, B, C。请表示:恰好有两个事件发生:
我们知道:两个事件同时发生可以用 来表示,但是怎么表示"恰好"呢?其实是类似地,我们只要令其中两件事件和另一个事件的对立事件同时发生就可以了!
例如:
表示的就是:A, B同时发生,
发生就代表C不会发生。
因此,最终的结果就是:
四、排列和组合的区别辨析
【1】排列:我们大学用 这样的形式来表示。我们具体看看这个式子的意义。
问题的背景是这样的:我们从4个人A, B, C, D里面选出2个人来排队拍照片,问有几种可能性?
我们现在的重点不是分析这道题的答案是多少,毕竟这是高中数学的基础题。我们想关心的,是使用排列的问题情况:在这道题目中,我们是先从4个人里面选2个,选完了还没完,这两个人的站位顺序还有讲究,比如说 和 就是两种不同的站法。
因此,顺序就成了排列的关键词。比如,如果题目中有“依次”,“按顺序”等词,那么很可能就用的是排列。因此,排列可以说成:从 个元素中选出 个不同的元素来排队,就是
【2】组合:有了排列的基础,组合就不难了:无非就是从 个元素中选出 个元素(取出来之后不用排队!)这就是
4.1 重要模型1——古典概型
古典概型必须满足下面两个条件:
- 每一个基本事件发生的概率都是相同的。
- 随机试验的结果是有限的
古典概型中计算事件 A 的概率,有一个公式:
下面引入几个重要的例题:(老师上课特别强调)
【抽球模型】袋子里面有 个黄球 个白球,从中接连任意抽取 个球,且每一次抽的球不放回去,问第 次抽到黄球的概率。
,这是一个古典概型,因此我们可以先考虑所有基本事件的数目。我们注意关键词:“接连”,也就是说,一个一个这样抽取,换句话说,如果我们是先一股脑从 个球中抽取出 个球,那么本题最终的结果还需要把一股脑抽出来的这 个球再进行排列!
因此,所有基本事件的情况数目就是:
下面我们继续看看第 球刚好抽到黄球的概率:我们这样想,因为最终呈现在我们眼前的,是一排已经排列好的 个球,那么其实我们也可以先从黄球中抽出一个放在 的位置上,再从剩下的球里面安排其他球的排列情况。
先从 个黄球里面取1个放在第 位可以表示成:
现在,总球数就是 了。我们要从这 个球中取出 个进行排列,可能的情况就可以表述成:
因此,最终的概率就可以表示成:
:既然我们刚刚说到了,最终这些球呈现在我们眼前的就是一串已经排列好的样子,其实谁先取出来的,谁后取出来的,我们都不知道,其实我们也不必关心。因为假设我们第一个取的球就是放在第 个位置的,那么也就是说先从 个球里面选出 1 个直接放在第 个位置就OK,其他一律不管。那么概率就可以表示为:
从上面这个抽球模型可以看出:如果都是按照这样的规则(一个人一个人按顺序抽球,抽出来的球不放回),那么每一个人抽到黄球的概率完全一样!不受抽球顺序影响!!
个质点在 N 个格子的分布问题:设有 个不同的质点,每一个质点落入格子的概率都一样,是 ,求以下事件的概率:
- 指定的 个格子中各有 1 个质点
- 随机的 个格子中各有1个质点
- 指定的一个格子中恰有 个质点( )
这依然是一个古典概型,我们首先计算出所有可能的情况。因为没有规定说一个格子里面能塞进几个质点,因此,我第一个质点有 N 个格子可以放,第二个质点依然也是有 N 个格子可以放、、、因此,基本事件的总数就是:
情况1:指定的 个格子中各有 1 个质点:如果我们把格子看成一排 个座位的位置,让 个观众入座,也就是一个全排列的问题,情况有: 种。因此,概率为:
情况2: 随机的 个格子中各有1个质点:也就是我们要先从剧院的 个席位中选择出 个位子,再安排这 个观众入座。只不过多了选位子这一步: ,概率为:
情况3:指定的一个格子中恰有 个质点( ):一个位置上有 个观众,wc…叠罗汉可以考虑一下hhh。那么同理,我们要先从 个观众里面选出 个重量级选手参与叠罗汉,即: ,这只是排好了这一个位置上的,还有 个观众等待安排。
因此,剩下的 个观众,每一个人都有 个位置可以选(因为它们也可以叠罗汉,不强求)。因此,剩下这些观众排序的情况就是: ,因此,最终的概率就是:
过生日问题:全班有 个人,一年365天,问全班至少有2人在同一天过生日的概率。
依旧是一个古典概型,但是这里如果我们采取正向求解会非常麻烦——因为是“至少”,也就是说可以2个人同一天,也可以3个人同一天,甚至全班都是同一天(纳尼!还有这种操作!)
因此,我们采取反向求解——先计算全班每一个人的生日都不一样的概率,再用1减。
那么,第一步依然是计算基本事件的数目:每一个人都可能在365天其中一天生日,因此,所有可能
的情况就有:
下面看看每一个人都不一样的情况:也就是从365天里面选出 天,再进行排列。(这个排列其实又是一个全排列):
因此,最终的概率为:
4.2 重要模型2——几何概型
几何概型的解法就是把具体的问题转化成几何模型:
- 一维:转换为线段长度
- 二维:转换为图形面积
- 三维:转换为立体体积
具体是几维的,有一个小窍门,就是看题目中隐藏的决定事件 发生的变量有几种。
下面举两个例子:1. 甲乙会面问题:甲乙两人在6:00~7:00 这一个小时内可能到达某地见面。并且我们约定:谁先到了就等谁 15min,15min 内等不到就走人。问甲乙两人成功见面的概率:
如果我们设甲到达的时间是 ,乙到达的时间是 ,那么甲乙在这一个小时内任意时刻都有可能到达,对吧。
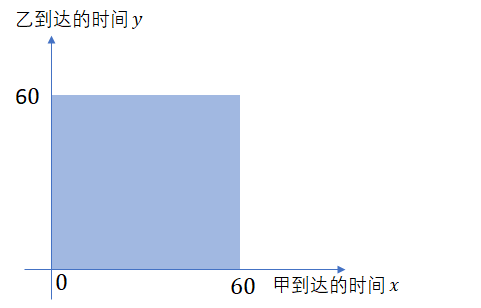
样本的全集就是这样一个正方形。
我们考虑两种情况:1 甲先到了,等乙15分钟;2 乙先到了,等甲15分钟
情况一:
;情况二:
,综合起来就是下面的表示:
下面我们就按照线性规划的思路,把这个线在全集上给它画出来:
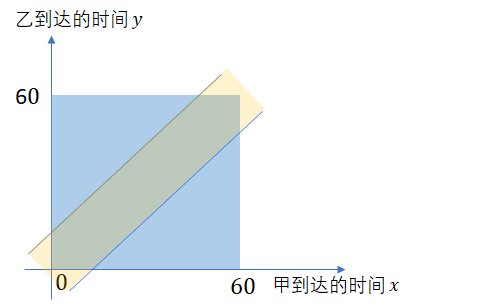
因此,经过简单的分析,我们就知道:甲乙顺利会面就是在黄色区域和蓝色区域相交的部分。
普丰投针试验:
现在有一个宽度为 的平面,和一个长度为 ( ) 的针,如下图:

现在把这个针随便扔,测量针的中心点与跟他较近的那一边的距离,记为: ,再记录针与相交边的夹角 ,问针与两条平行线相交的概率?
我们先看看这个针的落点到底有什么情况:
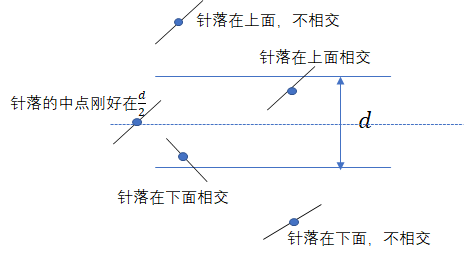
我们下面针对“针和线边缘相交的情况”分析一下:

我们很容易知道,夹角的范围就是 : ,x 的范围就是
x 与 φ 构成的平面就是我们的样本空间了
要使得针与边缘相交,我们还需要有:
最终,通过面积之比,我们就计算出了针与边缘相交的概率:
五、补充:蒙特卡洛方法介绍
我们上面提到了普丰投针试验的概率:
这是我们实际计算出来的,如果我们真的闲着没事儿,去亲自做了这个试验,假设我们一共试验了 次,针和边缘相交了 次,那么试验得到的概率就是:
理论上讲,我们的
越大,
就越接近 P。那么假如我们不知道
呢?那么我们就可以利用这样的性质:
因为这个式子里面除了
,其他的数字我们都是知道的,因此,我们就可以求出这个未知数。
这就是蒙特卡洛方法,通过统计试验去计算某些未知数的方法。
