【概率论与数理统计 Probability and Statistics 6】—— 连续型随机变量的分布

写在前面：在引入了连续型随机变量的概率密度函数 $f(x)$ 及其分布函数 $F(x)$ 之后，我们求概率就有了一个利器：积分。譬如：计算 $P\{a≤X≤b\}$ 的概率，我们可以表示成： $\int_a^bf(x)dx$，类似地，如果求 $P\{X≤b\}$，就是 $\int_{-∞}^bf(x)dx$

一、均匀分布

首先，我们看看满足均匀分布的概率密度函数： $f(x) = \begin{cases} \frac{1}{b-a}\quad a≤x≤b\\ 0\quad else\\ \end{cases}$
记作： $X$ ~ $U[a, b]$，下面我们来看看均匀分布的分布函数 $F(x)$：
【1】当 $x<a$ 时： $F(x) = 0$
【2】当 $a ≤ x < b$ 时： $F(x) = \int_{-∞}^af(x)dx+\int_{a}^xf(x)dx =\frac{x-a}{b-a}$
【3】当 $x≥b$ 时， $F(X) = 1$

下图是均匀分布的概率密度函数以及分布函数的图片：

说明一个技巧：当题目说了某一个事件服从均匀分布时，我们就可以找到这个随机变量 X 的范围，或者说区间。那么事件在这个区间的概率密度函数都是 区间长度的倒数。

二、指数分布

指数分布的概率密度函数表示为： $f(x) = \begin{cases} λe^{-λx} \quad x>0\\ 0\quad x ≤ 0 \end{cases}$
我们记作： $X$~ $EXP(λ)$，同样地，我们一起计算一下它的分布函数：
【1】当 $x<0$时， $F(x) = 0$
【2】当 $0 ≤ x$时， $F(x) = \int_{-∞}^0f(x)dx + \int_{0}^xλe^{-λx}dx =1-e^{-λx}$

2.1 指数分布的无记忆性

在上一篇 $Blog$ 里面，我们也介绍了几何分布的无记忆性。对于指数分布，也是有一样的性质。即表示为： $P\{X>s+t|X>s\} = P\{X>t\}$
我来解释解释这个式子，我们知道，对于寿命类问题常常满足指数分布。那么我们就以灯泡的寿命为例：

我们具体化一下，假设 $s = 1000$， $t = 10$。那么上面的式子中， $P\{X>s+t|X>s\}$ 可以解释成：灯泡在已经用了 1000 小时之后，还能继续用 10 小时的概率。

$P\{X>t\}$ 可以解释成：灯泡刚买回来，（没用过的前提下）可以用 10 个小时的概率。

也就是说，只要你这个灯泡现在这个时刻是好的，那么不管你以前亮了多久，以后亮相同时间的概率完全一样！

我们证明一下：首先是等式的左边 $P\{X>s+t|X>s\}$
$P\{X>s+t|X>s\} = P\{\{X>s+t\}∩\{X>t\}\}$
我们画一下这两个区间 $\{X>s+t\}$ 和 $\{X>t\}$ 的 交集，我们就会发现： $P\{X>s+t|>s\} = P\{X>s+t\}$
$P\{X>s+t\} = \int_{s+t}^{+∞}λe^{-λx}dx =e^{-λt}$
同理我们可以计算得到： $P\{X>t\} = e^{-λt}$

三、正态分布（important）

3.1 一般正态分布

对于一般的正态分布，我们的概率密度函数用小写字母： $φ$ 表示，即： $φ(x) = \frac{1}{\sqrt{2π}σ}e^{-\frac{(x-μ)^2}{2σ^2}}$
注意：那个 $σ$ 是在根号外面的！! 这个式子相当难记忆，不过没关系，我们最重要的只是把 $μ$， $σ$ 找出来就可以了。一般记为： $X$ ~ $N(μ, σ^2)$

下面我们看看这个概率密度函数都有什么性质：

【性质1】： $\int_{-∞}^{+∞}φ(t)dt=1$ 这个很显然，总概率是1 没毛病，但是想要证明还是不容易的，这需要我们在微积分里面的一个结论： $\int_{-∞}^{+∞}e^{-x^2}dx = \sqrt{π}$
这个式子大家还是需要记忆一下的，毕竟这货挺难算的hhh，证明的话，我们简单看看吧： $\begin{aligned} &\quad\frac{1}{\sqrt{2π}σ}\int_{-∞}^{+∞}e^{-(\frac{t-μ}{\sqrt{2}σ})^2}dt\\ &=\sqrt{2}σ\frac{1}{\sqrt{2π}σ}\int_{-∞}^{+∞}e^{-(\frac{t-μ}{\sqrt{2}σ})^2}d(\frac{t-μ}{\sqrt{2}σ})\\ &=\frac{1}{\sqrt{π}}\sqrt{π} = 1 \end{aligned}$

【性质2】：这个正态分布的概率密度函数关于 $μ$ 对称，这个好理解，因为有： $(x-μ)^2$这一项

当 $x = μ$ 时， $φ(x)$ 取得最大值： $\frac{1}{\sqrt{2π}σ}$

【性质 3】正态分布的概率密度函数以 x 轴作为渐近线

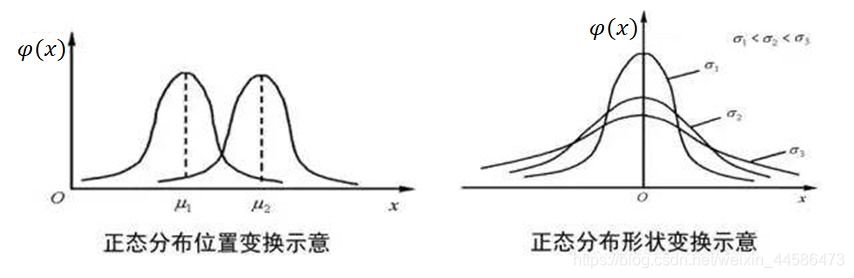
【性质 4】当 $σ$ 固定时，改变 $μ$ 的大小将会导致 $φ(x)$ 沿着水平方向左右平移。
另外，当 $μ$固定，也就是曲线的对称轴不变的时候，如果 ：

1. $σ$ 增大，那么函数的峰值降低，函数变胖，注意任何形状的函数与 x 轴围成的面积都是一样的 1
2. $σ$ 减小，函数的峰值增大，函数形状得高瘦
   

对于一般正态分布的分布函数，还是一样的按照定义积分： $Ф(x) = \int_{-∞}^xφ(t)dt$
不过这个式子积不出来，所以我们一般很少用到。

3.2 标准正态分布

当 $μ$ = 0， $σ = 1$ 时，我们成为标准正态分布。即： $X$ ~ $N(0, 1)$，分别把 $μ$ = 0， $σ = 1$ 带入上面一般正态分布的概率密度函数，我们可以得到标准正态分布的概率密度函数： $φ_0(x) =\frac{1}{\sqrt{2π}}e^{-\frac{x^2}{2}}$

它也有几个性质，我们一起来看看：
【性质1】： $φ_0(x)$ 是钟形曲线，而且是偶函数，即 $φ_0(x) = φ_0(-x)$

【性质2】（重要）： $Ф_0(x) = 1 - Ф_0(-x)$

【性质3】一般我们计算正态分布的概率，用的也是查表。一般来讲，表中只给了 $0≤x≤5$的值，当 $x>5$ 时，我们认为： $φ_0(x) = 0$， $Ф_0(x) = 1$；当 $x<-5$ 时，我们认为： $φ_0(x) = 0$， $Ф_0(x) = 0$

当 $-5<x≤0$ 时，要计算 $Ф_0(x)$，我们可以先通过： $1-Ф_0(-x)$ 反向求得

3.3 一般正态分布化为标准正态分布

这里我直接把在纸上演算的过程贴上来（公式打起来太费劲了hhh）：

接下来是分布函数的转换：

我们发现，对于概率密度函数而言，出了把 $φ$ 里面的变量换成： $\frac{x-μ}{σ}$，还需要补一个系数 $\frac{1}{σ}$，而对于分布函数的转换，就直接把变量改写成： $\frac{x-μ}{σ}$ 就OK

我们举几个例子看看：
【例子一】：假设 $X$ ~ $N(1,4)$，求： $P\{0<X≤1.6\}$
首先明确，这是一个一般的正态分布，且 $μ = 1$， $σ = 2$。

$P\{0<X≤1.6\} = = Ф(1.6) - Ф(0)$

此时，我们还需要把它转化为标准正态分布，因此有： $Ф(1.6) = Ф_0(\frac{1.6-1}{2}) = Ф_0(0.8)\\ \quad\\ Ф(0) = Ф_0(\frac{0-1}{2}) = Ф_0(-0.5)$

所以原式子变为： $Ф(1.6) - Ф(0) = Ф_0(0.8) - Ф_0(-0.5) = Ф_0(0.8) - 1 + Ф_0(0.5)$

3.4 3σ准则

这个准则有一张图就能解释明白：

也就是说事件发生在 ： $μ-3σ ≤ X ≤ μ +3σ$ 的概率是 99.73%，概率非常高。