概率论与数理统计知识点(三) 连续型随机变量及其概率密度

1. 随机变量的分布函数

• 背景： 对于非离散型的随机变量 $X$，其取值不能一一列举出来，因此就不能像离散型随机变量那样使用分布律描述它。非离散型随机变量有很多种，其中连续型随机变量极其常见，因此我们重点研究连续型随机变量。对于连续性随机变量，在某个点的概率为 $0$，另外，实际中，对于元件的寿命，测量的误差等，研究其落在某个区间的概率更有意义，因此我们引出了随机变量的分布函数

• 定义： 设 $X$是一个随机变量， $x$ 是任意实数，函数 $F(x)=P\{X \leq x\}, -\infty<x<\infty$ 则为 $X$的分布函数。

  虽然对于离散型随机变量，我们可以使用分布律来全面地描述它，但为了从数学上能够统一地对随机变量进行研究，因此，我们针对离散型随机变量和非离散型随机变量统一地定义了分布函数。

• 性质

  $1^o \quad F(x)$是一个不减函数

  对于任意实数 $x_1,x_2(x1<x_2)$,有 $F(x_2)-F(x_1) = P\{x_1<X \leq x_2\} \geq 0$ 成立

  $2^o\quad$ $0\leq F(x)\leq 1，\quad F(-\infty) = 0，\quad F(\infty) = 1$

  $3^o\quad$ $F(x+0)=F(x)$, 即 $F(x)$ 是右连续的

• 用分布函数表示事件概率

  • $P\{X\leq b\}=F(b)$
  • $P\{X> a\}=1-P\{X\leq a\} = 1-F(a)$
  • $P\{ a<X\leq b\}=P\{X\leq b\}-P\{X<=a\} = F(b)-F(a)$
  • $P\{X< b\}=F(b-0)$
  • $P\{X\geq b\}=1-P\{X< b\} = 1- F(b-0)$
  • $P\{X = b\}=P\{X \leq b\}-P\{X < b\} = F(b)-F(b-0)$
  • 注意

  1. 这里的 $F(b-0)$表示 分布函数 $F(x)$ 在 $x=b$处理左极限。 同理， $F(b+0)$表示 分布函数 $F(x)$ 在 $x=b$处理右极限 。
  2. 细心的同学也许注意到背景部分提到连续型随机变量在某一个点的概率为0，这里还整 $F(b-0)$ 和 $F(b+0)$ 搞这么麻烦是为了啥？ 原因是这部分内容，对连续型和离散型随机变量都成立，离散型随机变量在某一个点有具体的不为0的概率值，因此不能忽略！

2. 连续型随机变量及其概率密度

• 定义，如果随机变量 $X$的分布函数 $F(x)$,存在非负函数 $f(x)$，使对于任意实数 $x$有 $F(x)=\int_{-\infty}^xf(t)dt,$ 则称 $X$ 为连续型随机变量 ，其中函数 $f(x)$称为 $X$的概率密度函数，简称概率密度

• 概率密度具有以下性质：

  $1^o\quad$ $f(x)\geq0$

  $2^o\quad$ $\int_{-\infty}^{+\infty}f(x)dx=1$

  $3^o\quad$ 对于任意实数 $x_1,x_2(x_1\leq x_2)$ ， $P{x_1< X\leq x_2}=F(x_2)-F(x_1)= \int_{x_1}^{x_2}f(x)dx;$

  $4^o\quad$ 若 $f(x)$在 $x$处连续，则有 $F^{\prime}(x)=f(x).$

• 连续型随机变量 $X$，任取一个指定实数 $a$的概率为 $0$，即 $P\{X=a\}=0$

  证明如下：

  根据分布函数定义，有 $P\{X = a\}=P\{X \leq a\}-P\{X < a\} = F(a)-F(a-0)$ ,我们知道 $F(a-0)$ 表示 $F(x)$ 在 $x=a$处理左极限，即 $\lim\limits_{x\rightarrow a^-}F(x)$ , 由于 $F(x)$ 在定义域内连续，所以有 $F(a-0)=\lim\limits_{x\rightarrow a^-}F(x)=F(a)$ . $\therefore P\{X = a\}= F(a)-F(a-0) = 0$

  相关推论：

  1. 这里虽然 $P\{X=a\}=0$ , 但随机变量 $X$是可以取到 $a$ 点的， 也就是说 对于事件 $A$，如果其发生的概率 $P(A)=0$, $A$不一定是 不可能事件， 但是如果已经知道 $A$ 是不可能事件，则必有 $P(A)=0$

  2. 连续型随机变量，计算区间概率时，区间端点可有可无，即 $P\{a<X\leq b\} = P\{a\leq X\leq b \}=P\{a\leq X<b\}=P\{a\leq X<b\}$ .

  3. 由第二条可知，我们假设 $P\{a<X\leq b\} = P\{a\leq X\leq b \}=1$, 会发现虽然 $P\{a<X\leq b\}=1$， 但是却不能取到 $a$ 点，所以得出结论：对于事件 $A$，如果其发生的概率 $P(A)=1$，则 $A$不一定是必然事件，但是如果已经知道 $A$ 是必然事件，则必有 $P(A)=1$.

3. 重要的连续型随机变量分布

3.1 均匀分布

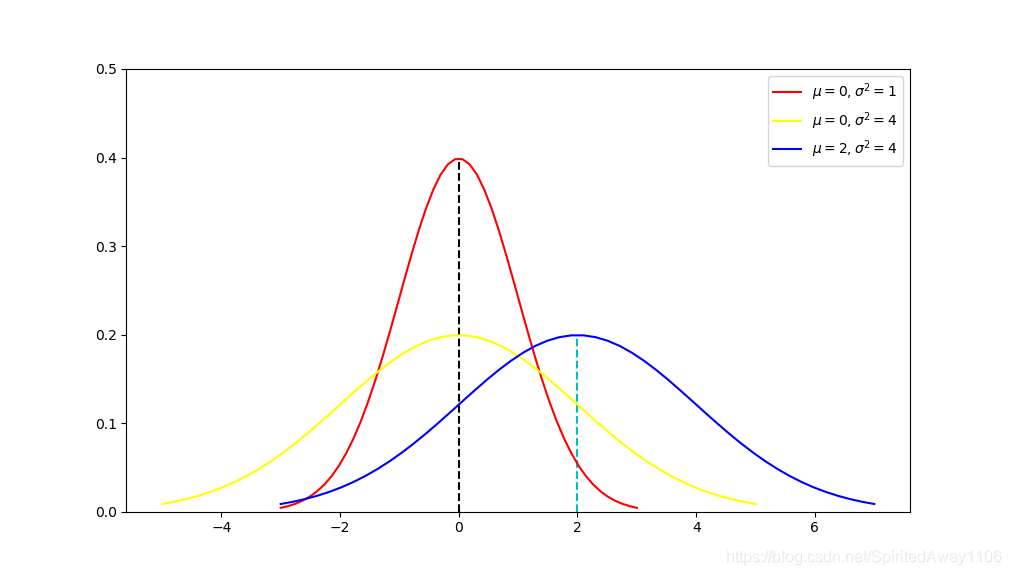
• 若连续型随机变量 $X$具有概率密度 $f(x)=\begin{cases} \frac{1}{b-a},\quad a<x<b， \\ 0,\quad else \end{cases}$ 则称 $X$在区间 $(a,b)$ 上服从均匀分布，记作 $\pmb{X\sim U(a,b)}$

  必要性证明

  $\begin{aligned}\int_{-\infty}^{+\infty}f(x)dx = \int_{-\infty}^{a}0dx+\int_{a}^{b}\frac{1}{b-a}dx+\int_{b}^{+\infty}0dx = \left.\frac{x}{b-a}\right|_a^b = 1 \end{aligned}$

• 分布函数

  $\begin{aligned}F(x) = \begin{cases} 0,\quad & -\infty<x\leq a, \\ \frac{x-a}{b-a},\quad & a< x <b, \\ 1,\quad & x\geq b. \end{cases}\end{aligned}$

• 性质

  落在 $(a,b)$子区间内的概率，只跟子区间长度有关，跟子区间位置无关，证明很简单，不再赘述

• 应用

  在公交站台的等车时间，针落在坐标纸上的倾斜角等

3.2 指数分布

• 若连续型随机变量 $X$具有概率密度 $\begin{aligned}f(x)=\begin{cases} \frac{1}{\theta}e^{-x/\theta},\quad 0<x， \\ 0,\quad else \end{cases}\end{aligned}$ 其中 $\theta>0$为常数，则称 $X$服从参数为 $\theta$的指数分布，记作 $\pmb{X\sim E(\theta)}$

  必要性证明

  $\begin{aligned} \int_{-\infty}^{+\infty}f(x)dx = \int_{-\infty}^{0}0dx+\int_{0}^{+\infty}\frac{1}{\theta}e^{-x/\theta}dx = \left.-e^{-\frac{x}{\theta}}\right|_0^{+\infty} = 1 \end{aligned}$

• 分布函数

  $\begin{aligned} F(x) = \begin{cases} 1-e^{-x/\theta},\quad &x>0 \\0,\quad &else. \end{cases} \end{aligned}$

• 性质

  无记忆性，如果 $X$是某一元件的寿命，那么已知原件已经使用了 $s$小时，它总共能用至少 $s+t$ 小时的条件概率，与从开始使用时算起它至少能用 $t$ 小时的概率相等，数学表达式为 $P\{X>s+t|X>s\} = P\{X>t\}$

  证明如下

  $\begin{aligned} P\{X>s+t|X>s\} &= \frac{P\{(X>s+t)\cap (X>s)\}}{P\{X>s\}} \\ &=\frac{P\{X>s+t\}}{P\{X>s\}} \\&= \frac{1-F(s+t)}{1-F(s)} \\&= \frac{1-(1-e^{-(s+t)/\theta})}{1-(1-e^{-(s)/\theta})} \\&= e^{-t/\theta} = P\{X>t\}\end{aligned}$

• 应用

  服务系统的服务时间，通话时间，某消耗品的寿命等

3.3 正态分布

• 若连续型随机变量 $X$具有概率密度 $\begin{aligned}f(x)= \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} , \quad -\infty<x<+\infty \end{aligned}$ 其中 $\mu,(\sigma>0)$为常数，则称 $X$服从参数为 $\mu,\sigma$的正态分布或高斯(Gauss)分布，记作 $\pmb{X\sim N(\mu,\sigma^2)}$

  必要性证明

  很明显 $f(x)\geq0$, 下面证明 $\int_{-\infty}^{+\infty}f(x)dx=1$

  令 $\frac{x-\mu}{\sigma} = t$ ，则 $f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{t^2}{2}}, dx = \sigma dt$

  $\begin{aligned} \int_{-\infty}^{+\infty}f(x)dx = \int_{-\infty}^{+\infty} \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{t^2}{2}}\sigma dt = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty} e^{-\frac{t^2}{2}}dt \end{aligned}$

  我们先求 $\int_{-\infty}^{+\infty} e^{-\frac{t^2}{2}}dt$ 的积分，很难直接求出其积分，我们需要用到一个技巧，令 $I=\int_{-\infty}^{+\infty} e^{-\frac{t^2}{2}}dt$

  $\begin{aligned} I^2 &= \int_{-\infty}^{+\infty} e^{-\frac{t^2}{2}}dt \cdot\int_{-\infty}^{+\infty} e^{-\frac{u^2}{2}}du \quad(定积分的值与积分变量无关，与被积函数和积分上下限有关) \\&= \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} e^{-\frac{t^2+u^2}{2}}dtdu \\&=\int_{0}^{2\pi}\int_{0}^{+\infty} \rho e^{-\frac{\rho^2}{2}}d\rho d\theta \quad(利用极坐标求解定积分值) \\&=\int_{0}^{2\pi} -e^{-\frac{\rho^2}{2}}|_0^{+\infty} d\theta = \int_{0}^{2\pi}1d\theta \\&= 2\pi \\ &\because I=\int_{-\infty}^{+\infty} e^{-\frac{t^2}{2}}dt>0 \quad \therefore I = \sqrt{2\pi} \end{aligned}$

  $\begin{aligned} \therefore \int_{-\infty}^{+\infty}f(x)dx = \frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{+\infty} e^{-\frac{t^2}{2}}dt = \frac{1}{\sqrt{2\pi}} \cdot {\sqrt{2\pi}} = 1 \end{aligned}$

• 分布函数

  $F(x) = \frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{x}{-\frac{(t-\mu)^2}{2\sigma^2}}dt$

• 性质

  $1^o\quad$ 正态分布曲线关于 $x=\mu$ 对称.

  $2^o\quad$ 当 $x=\mu$ 时取得最大值， $f(\mu)=\frac{1}{\sqrt{2\pi}\sigma}$

  其他特性，可参考下图理解

  1. 曲线在 $x=\mu\pm\sigma$ 处有拐点
  2. 曲线以 $0x$轴为渐近线
  3. $x$离 $\mu$越远， $f(x)$的值就越小，这表明对于同样长度的区间，当区间离 $\mu$越远， $X$落在这个区间的概率就越小
  4. 如果固定 $\sigma$,改变 $\mu$的值，则图形沿着 $0x$轴平移，而不改变其形状。 $\mu$被称作位置参数(参考下图黄色和蓝色的线)
  5. 如果固定 $\mu$,改变 $\sigma$的值，由于其最大值 $f(\mu)=\frac{1}{\sqrt{2\pi}\sigma}$ 随着 $\sigma$变小，而变得越尖，因而 $X$落在 $\mu$附近的概率变大 (参考下图红色和黄色的线)
     

• 当 $\mu=0,\sigma=1$ 时称随机变量 $X$服从标准正态分布，其概率密度和分布函数分别用 $\phi(x)$和 $\Phi(x)$表示，则有 $\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$,

  $\Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}{-\frac{t^2}{2}}dt$ , 由性质很容易推知: $\Phi(-x)=1-\Phi(x)$

• 引理，若 $X\sim N(\mu,\sigma)$,则 $Z=\frac{X-\mu}{\sigma} \sim N(0,1)$.

  证明如下：

  $Z=\frac{X-\mu}{\sigma}$的分布函数为

  $\begin{aligned}P\{Z\leq x\}&=P\{\frac{X-\mu}{\sigma}\leq x\}=P\{X\leq \sigma x+\mu\}\\&=\int_{-\infty}^{\sigma x+\mu}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt = F(x) \\ \therefore &f(x) = F'(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} = \phi(x) \quad(变上限积分求导规则：上限带进去乘以上限对变量求导) \\\therefore 命题得证 \end{aligned}$

  第二种证明方法， 令 $\frac{t-\mu}{\sigma}=u,$ 则

  $\begin{aligned}P\{Z\leq x\}&=\int_{-\infty}^{\sigma x+\mu}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt \\&= \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{u}e^{-\frac{u^2}{2}}du =\Phi(x) \\ \therefore 命题得证 \end{aligned}$

  由该引理可知 $F(x)=P\{X\leq x\} = P\{\frac{X-\mu}{\sigma}\leq \frac{x-\mu}{\sigma}\} = \Phi(\frac{x-\mu}{\sigma})$

  $P\{x_1\leq X\leq x_2\}=P\{\frac{x_1-\mu}{\sigma} \leq \frac{X-\mu}{\sigma}\leq \frac{x_2-\mu}{\sigma}\} = \Phi(\frac{x_2-\mu}{\sigma})-\Phi(\frac{x_1-\mu}{\sigma})$

  $P\{\mu-\sigma\leq X\leq \mu+\sigma\} = \Phi(1)-\Phi(-1) = 2\Phi(1)-1 = 68.26\%.$

  $P\{\mu-2\sigma\leq X\leq \mu+2\sigma\} = \Phi(2)-\Phi(-2) = 2\Phi(2)-1 = 95.44\%.$

  $P\{\mu-3\sigma\leq X\leq \mu+3\sigma\} = \Phi(3)-\Phi(-3) = 2\Phi(3)-1 = 99.74\%.$

  我们看到，正态分布的值落在 $(\mu-3\sigma, \mu+3\sigma)$内几乎时肯定的事情，这就是 $\pmb{3\sigma}$法则

• 设 $X\sim N(0,1)$，若 $z_a$ 满足条件 $P\{X>z_a\}=a, \quad 0<a<1，$则称点 $z_a$为标准正态分布的上 $\pmb{\alpha}$分位点

• 应用

  在自然现象和社会现象中，大量随机变量都服从或者近似服从正态分布。例如，一个地区的男性成年人身高，测量某零件长度的误差，海洋波浪的高度，半导体器件中的热噪声电流或电压等。 后续我们还会介绍正态分布的其他重要特性