一、0-1 分布

所谓的 0-1 分布，大家要记住它的几个特点：

随机变量 X 只取 0 或 1 两种值。所以结果也只有两种（概率分布是 $p$ 和 $1-p$ ）
我们的随机试验只做 1 次

二、二项分布

和 0-1 分布有相似之处，也有不同之处。相似点在于随机变量依然也是两种 X = 0 或 1 （概率分布就是 $p$ 和 $1-p$ ），但是不同之处在于此时我们的随机试验是做了 $n$ 次，其中事件 X 发生了 $k$ 次。

用公式表示也很简单，设 $P\{A = k\}$ 表示在 $n$ 次实验里面，事件A发生了 $k$ 次的概率，那么： $P\{A = k\} = C_n^kp^k(1-p)^{n-k}$
其中， $p$ 是事件 A 发生的概率。上式也记作： $X$ ~ $B(n,p)$

但是二项分布在应用的时候有些困难，难在计算，当我们的 k 很大的时候，往往这个概率值是很难计算出来的

三、泊松分布

大家需要记忆泊松分布的概率分布函数： $P\{X=k\} = \frac{λ^k}{k!}e^{-λ}\quad(k=0,1,2,3,\cdots)$
这里的 λ 是一个常数。泊松分布我们记为： $X$ ~ $Pios(λ)$ 。这个分布在什么场景下可以用得上呢？
一般是在生活场景：例如电话呼叫台、公交站等车、、、

注意：下面介绍泊松分布的巨大优势，还记得我们上文说二项分布有的时候那个概率值根本算不出来。那么，其实我们有一个泊松定理：当二项分布里面的 $n$ 比较大（试验次数比较多）， $p$ 比较小的时候，我们可以使用泊松分布来近似代替二项分布。（记得 $n$ 一定得大一点， $p$ 一定得小一点）

更具体地说：如果当 $np ≤ 10$ 时，我们有： $λ = np$ ，使用泊松分布来求解概率。泊松分布求概率是一件不困难的事情，因为我们有泊松分布表！下面展示了表的一部分，我们看看怎么查表：

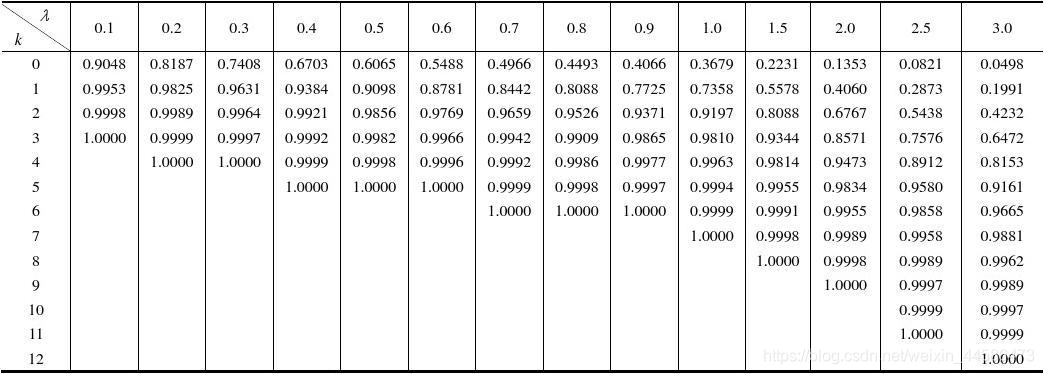
在这里插入图片描述
看一个例题：

设每次击中目标的概率是0.001，且各次射击是否击中目标可以看作互相没有影响，如果射击5000次，求：
（1）击中12次的概率

首先我们分析啊：射击这玩意儿结果不就两个嘛——击中和击不中，因此本题是符合二项分布的。
那么，首先设 $ξ$ 表示击中的数目。因此击中12次的概率就是： $P\{ξ = 12\} = C_{5000}^10.001^{12}9.999^{5000-12}$
这个复杂的式子根部无法计算，但是我们别忘了泊松定理：此处， $n=5000$ ， $p=0.001$ ， $np = 5$ ，满足泊松定理的条件，因此，λ = np = 5，有： $P\{ξ=12\} = \frac{5^{12}}{12!}e^{-5}$
我们就下来就可以查表了：找到 λ=5和 k =12对应的值，就是概率。

四、几何分布

首先，大前提依然是伯努利试验。假设成功的概率是 $p$ ，如果把 X 记为首次出现成功所需要的试验次数，那么，有： $P\{X=k\} = p(1-p)^{k-1}$
这个式子好理解：首先，我们现在是知道第 k 次试验是已经成功了，而且是首次成功。那么我们直接先把那一次成功的概率摆在第一个。反之，第 k 次试验才出现首次成功，意味着前面的 k-1 次都是不成功的。

4.1 几何分布的无记忆性

我们举一个有趣的例子理解一下：

现在假如你是一名“赌徒”，来到了赌场准备“大干一场”，你正在做的是 “赌大小”，而你现在已经连续 10 次押 “大”，然而结果全部都是 “小”。这时，你会怎么想？

如果是真赌徒，你可以会这么认为：都已经连续 10 把出现小了，那么之后再出现小的概率应该会很小，所以，你一口气把所有身家都投在了买 “大”。。。

而真实情况是：你是学过几何分布人，因此，你想了一下：你现在参与的这次赌注，结果要么大，要么小，这似乎符合几何分布，我们把几种情况列出来看看：
在这里插入图片描述
事实上，在前10次都是小的情况下，第 11 次出现大和直接第一次就出现大的概率完全一样！即：
$P\{X=11|X>10\} = P\{X=1\}$
这就是几何分布的无记忆性。