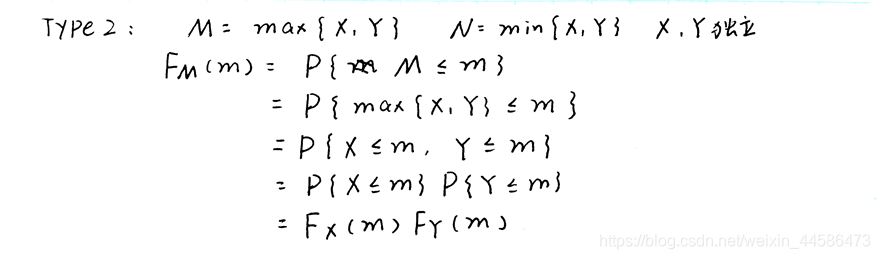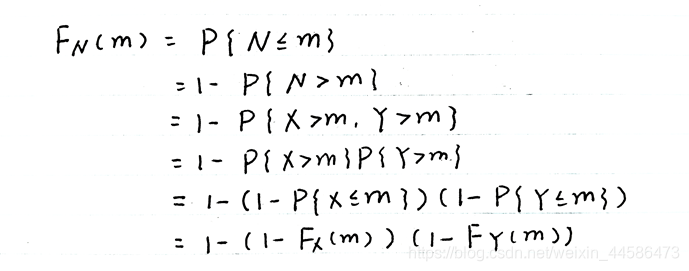【概率论与数理统计 Probability and Statistics 10】—— 二维随机变量函数的分布（离散型+连续型）

一、二维离散型随机变量函数的分布

这一部分非常简单，就是把 X, Y 带入 Z 的表达式，求出每一组（X, Y)对应的 Z 的值，然后把对应 X, Y 的联合概率对应着抄上去即可。但是要注意相同的 Z 需要合并！

二、二维连续型随机变量函数的分布和分布密度

首先，我们有两个随机变量 X, Y。它们的概率密度函数已知： $f(x, y)$，现在有一个 $Z = g(X, Y)$。那么如何计算 $f_Z(x, y)$

这种题目有两个步骤：1. 计算分布函数 $F_Z(z)$，2. 对分布函数求导得到密度函数 $f_Z(z)$
【1】求分布函数： $F_Z(z) = P\{Z ≤ z\} = P\{g(X, Y) ≤ z\} = \iint_{D_Z}f(x, y)dxdy$。其中区域 $D_Z = \{(x, y)|g(X, Y)≤ z\}$
【2】两边求导得到 $f_Z(z)$

那么，现在问题的关键就是如何找出并正确地画出区域 $D_Z = \{(x, y)|g(X, Y)≤ z\}$。由于二维连续型随机变量的函数会比较复杂，因此在课程范围内我们也只是讨论了几种常见的情况。诸如： $Z = X+Y, Z = max\{X, Y\}, Z = min\{X, Y\}\cdots$

我们下面通过例子来进一步说明：

$Z = X+Y$，求 $F_Z(z)$
下面我们给出推导：

至此，我们得到了两个重要公式——卷积公式： $f_Z(z) = \int_{-∞}^{+∞}f_X(x)f_Y(z-x)dx\\ \space\\ f_Z(z) = \int_{-∞}^{+∞}f_X(z-y)f_Y(y)dy$

特别说明：卷积公式只有在 $Z = X+Y$ ，且 X, Y独立的情况下才可以使用！！！

然后还需要注意的一点就是，假设我们使用了第一个卷积公式： $f_Z(z) = \int_{-∞}^{+∞}f_X(x)f_Y(z-x)dx$，那么我们需要考虑的变量取值范围就是： $x$ 的取值范围和 $z-x$ 的取值范围。

这里接着引出一个重要结论：若 X, Y 都服从正态分布： $X$~ $N(μ_1,σ_1^2)$； $Y$~ $N(μ_2,σ_2^2)$，X, Y 独立，若 Z = X+Y，那么 Z 也服从正态分布，且： $Z$ ~ $N(μ_1+μ_2, σ_1^2+σ_2^2)$ 这个性质完全可以通过上面的方法得到，这里不再赘述。但是对于 $e^{\frac{xxx^2}{2}}$这样形式的，通过配方法得到正态分布密度函数的表达式的技巧还是需要特别留意。

下面我们再看看另一种类型的：