傅里叶级数和傅里叶变换之间的关系推理及应用

傅里叶级数和傅立叶变换是傅里叶分析的两个主要工具，它们之间有密切的关系。

什么是傅里叶级数

傅里叶级数是将一个周期函数分解为一系列正弦和余弦函数的和。它适用于周期性信号，可以将周期函数表示为一组振幅和相位不同的谐波分量的和。傅里叶级数展示了一个周期函数在不同频率上的频谱内容。这样说太学究了，刚开始接触的人的可能看到这就头大了……

所以傅里叶级数到底是什么呢？

引子：

我们平时理解的更多是平面中的点，一个数A，都可以找到一些数B,C线性组合相加等于A，$A=k_{1}B+k_{2}C$。$k_1,k_2是常数$。我们将$k_1,k_2$改写一下，$A=Bx+Cy$，变成了我们熟悉的形式。一个正交坐标系可以描述平面上的任意一点。

平面坐标系找到一组正交x,y即可以线性组合拟合A。如果A代表的不是一个数，是一个函数呢？是不是也可以找到类似的正交系x,y。但是函数的一组正交系是什么呢？

周期性函数呢？周期性函数可是有无数个点呀？用什么去拟合呢，此时可能看到这个问题的你在内心里已经有了一些小的想法了，就是找到一组周期性线的函数去拟合。

傅里叶老前辈找到了帮我们找到了，就是下列的三角函数！！！！！！！
$1，\cos (x)，\sin (x)，\cos (2x)，\sin (2x)，\dots ，\cos (nx)，\sin (nx)$，… 称为三角函数系。

傅立叶级数可以用以下公式表示：

$f_T(x)=\frac{a_0}{2}+{\sum }_{n=1}^N\left(a_n\cos \left(\frac{2\pi n}{T}x\right)+b_n\sin \left(\frac{2\pi n}{T}x\right)\right)$

展开写理解起来会容 易一些：

扫描二维码关注公众号，回复： 15456546 查看本文章

---

$$\begin{gathered} f(x_0)=\frac{a_0}{2}+a_1\cos \left(\frac{2\pi n_1}{T}{x}_0\right)+b_1\sin \left(\frac{2\pi n_1}{T}{x}_0\right)+a_2\cos \left(\frac{2\pi n_2}{T}{x}_0\right)+b_2\sin \left(\frac{2\pi n_2}{T}{x}_0\right) \\ +\dots \\ +a_N\cos \left(\frac{2\pi N}{T}{x}_0\right)+N\sin \left(\frac{2\pi N}{T}{x}_0\right) \end{gathered}$$

---

$$\begin{gathered} f(x_1)=\frac{a_0}{2}+a_1\cos \left(\frac{2\pi n_1}{T}{x}_1\right)+b_1\sin \left(\frac{2\pi n_1}{T}{x}_1\right)+a_2\cos \left(\frac{2\pi n_2}{T}{x}_1\right)+b_2\sin \left(\frac{2\pi n_2}{T}{x}_1\right) \\ +\dots \\ +a_N\cos \left(\frac{2\pi N}{T}{x}_1\right)+N\sin \left(\frac{2\pi N}{T}{x}_1\right) \end{gathered}$$

---

$$\begin{gathered} f(x_2)=\frac{a_0}{2}+a_1\cos \left(\frac{2\pi n_1}{T}{x}_2\right)+b_1\sin \left(\frac{2\pi n_1}{T}{x}_2\right)+a_2\cos \left(\frac{2\pi n_2}{T}{x}_2\right)+b_2\sin \left(\frac{2\pi n_2}{T}{x}_2\right) \\ +\dots \\ +a_N\cos \left(\frac{2\pi N}{T}{x}_2\right)+N\sin \left(\frac{2\pi N}{T}{x}_2\right) \end{gathered}$$

---

$⋮$

---

$$\begin{gathered} f(x_N)=\frac{a_0}{2}+a_1\cos \left(\frac{2\pi n_1}{T}{x}_N\right)+b_1\sin \left(\frac{2\pi n_1}{T}{x}_N\right)+a_2\cos \left(\frac{2\pi n_2}{T}{x}_N\right)+b_2\sin \left(\frac{2\pi n_2}{T}{x}_N\right) \\ +\dots \\ +a_N\cos \left(\frac{2\pi N}{T}{x}_N\right)+N\sin \left(\frac{2\pi N}{T}{x}_N\right) \end{gathered}$$

---

这里的合成的概念是时域上的叠加的概念，图片来源wikipedia

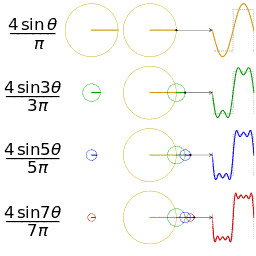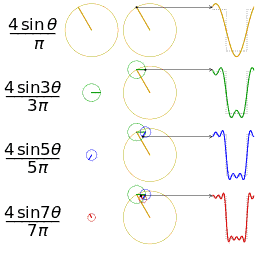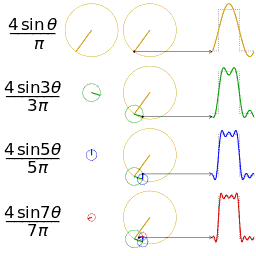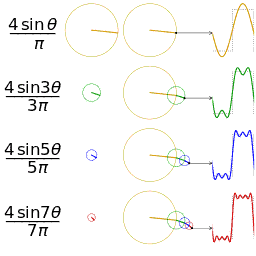
其中，$f(x)$是周期为$T$的函数，$a_0$是直流分量（平均值），$a_n$和$b_n$是傅立叶系数，表示在频率为$\frac{2\pi n}{T}$的正弦和余弦函数的振幅。这个公式表示了周期函数$f(x)$可以由一系列不同频率的正弦和余弦函数的和来逼近。

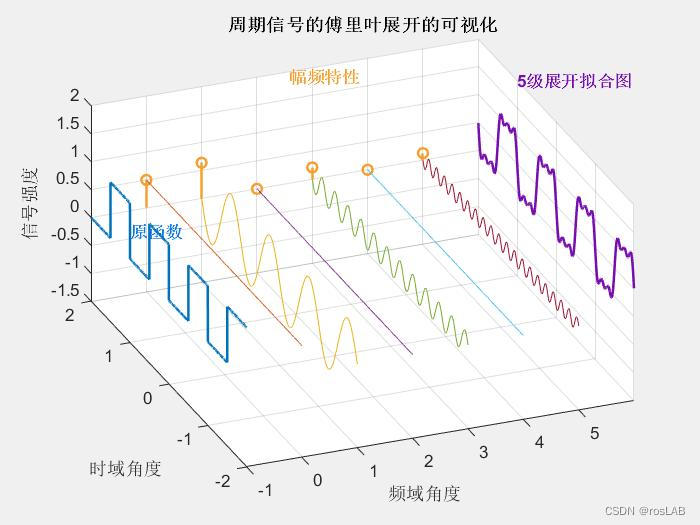
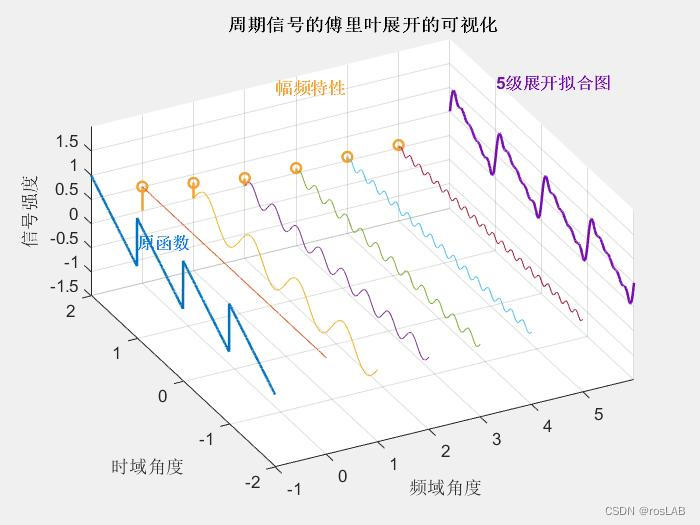
为什么可以这样展开

傅里叶级数的证明是一个相对复杂的过程，涉及到数学分析和傅里叶变换的理论。这里我将提供一个简要的概述，介绍傅里叶级数的基本思想和证明思路。
傅里叶级数的证明基于以下两个主要思想：

• 正交性：傅里叶级数利用了三角函数的正交性质。正弦和余弦函数在一个周期内是正交的，即它们的内积在不同频率下为零，而在相同频率下非零。这意味着不同频率的正弦和余弦函数是线性无关的基函数，可以用来表示不同频率的分量。
• 逼近性：傅里叶级数的另一个关键思想是逼近函数的概念。根据逼近定理，任何一个具有有限能量的周期函数，都可以用无限多个正弦和余弦函数的线性组合来逼近。通过增加正弦和余弦函数的振幅和相位，可以越来越接近原始函数。

基于这两个思想，傅里叶级数的证明过程可以大致概括为以下步骤： 首先，我们考虑一个周期为T的函数f(x)。我们要证明，可以将它表示为一系列正弦和余弦函数的和。 假设f(x)可以表示为以下形式的级数：
$f(x)=\frac{a_0}{2}+{\sum }_{n=1}^{\infty }(a_n\cos ({\omega }_{n}x)+b_n\sin ({\omega }_{n}x))$
其中，$a_0$、$a_n$、$b_n$是待定的系数，${\omega }_n$是频率。

接下来，我们将使用正交性质来计算各个系数。通过将f(x)与正弦和余弦函数进行内积运算，并利用正交性质，我们可以得到各个系数的表达式。

通过计算内积，我们可以得到以下公式

$a_0=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\cos ({\omega }_{n}x)dx,{\omega }_n=0$

$a_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\cos ({\omega }_{n}x)dx$

$b_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\sin ({\omega }_{n}x)dx$

${\omega }_n=\frac{2\pi n}{T}$

其中，$a_0$是直流分量，$a_n$和$b_n$是频率为${\omega }_n$的余弦和正弦分量的振幅。

由欧拉公式：

$\cos \theta =\frac{e^{i\theta }+e^{-i\theta }}{2}$

$\sin \theta =-i\frac{e^{i\theta }-e^{-i\theta }}{2}$

下面的证明摘抄自复变函数与积分变换的教材：

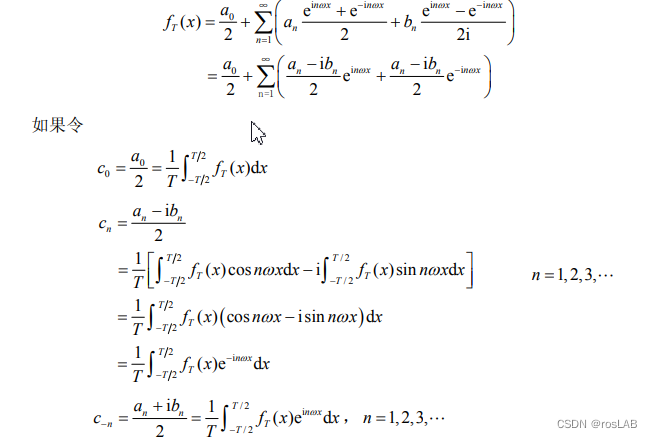
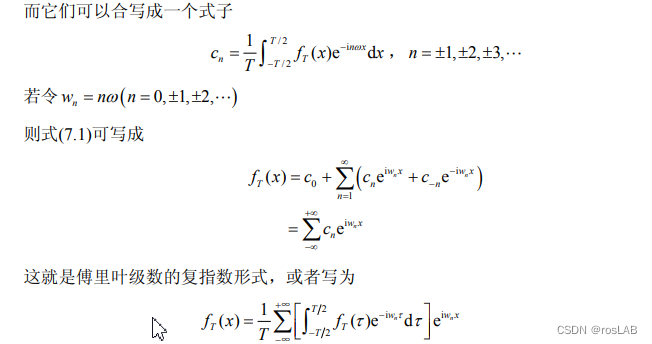
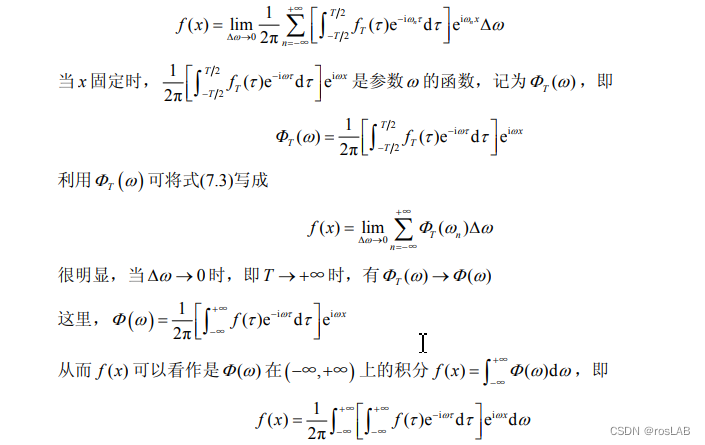
$F(\omega )={\int }_{-\infty }^{\infty }f(t)e^{-j\omega t}dt$

就是傅里叶变换了

什么是傅里叶变换

傅里叶变换则是将非周期性函数或信号分解为一组连续的正弦和余弦函数（复指数函数）的积分。傅立叶变换将一个时域函数转换为频域函数，显示了信号在不同频率上的频谱特征。

$F(\omega )={\int }_{-\infty }^{\infty }f(t)e^{-j\omega t}dt$
$\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(\omega )e^{j\omega t}d\omega$

---

$f_T(x)=\frac{a_0}{2}+{\sum }_{n=1}^N\left(a_n\cos \left(\frac{2\pi n}{T}x\right)+b_n\sin \left(\frac{2\pi n}{T}x\right)\right)$

两者之间的关系可以用以下方式表达：

傅里叶级数是傅立叶变换的一种特殊情况。当一个周期为T的函数被表示为傅里叶级数时，其傅立叶变换是一个离散的频谱，只包含一系列离散的频率分量。

对于一个连续非周期函数，傅立叶变换将其表示为一个连续的频谱，包含了所有可能的频率分量。这相当于将傅里叶级数中的频率分量离散化为连续的频谱。

傅立叶变换可以视为傅里叶级数的极限情况，当周期趋向于无穷大时，傅里叶级数的频率间隔趋向于零，从而得到了连续的频谱。

总的来说，傅里叶级数和傅立叶变换是傅里叶分析的两种表示方法，它们可以相互转换，但适用于不同的函数类别和分析需求。傅里叶级数适用于周期函数的频谱分析，而傅立叶变换适用于非周期函数的频谱分析。

FFT快速傅里叶变换

DFT定义：

$X_k={\sum }_{n=0}^{N-1}{x}_n{e}^{-i\frac{2\pi n}{N}k}，k=0,1,\dots ,N-1$

展开各项：

$X_0=x_0{e}^{-i\frac{2\pi 0}{N}k}+x_1{e}^{-i\frac{2\pi 1}{N}k}+\cdots +x_{N-1}{e}^{-i\frac{2\pi (N-1)}{N}k},k=0$
$X_1=x_0{e}^{-i\frac{2\pi 0}{N}k}+x_1{e}^{-i\frac{2\pi 1}{N}k}+\cdots +x_{N-1}{e}^{-i\frac{2\pi (N-1)}{N}k},k=1$
$\dots$
$X_{N-1}=x_0{e}^{-i\frac{2\pi 0}{N}k}+x_1{e}^{-i\frac{2\pi 1}{N}k}+\cdots +x_{N-1}{e}^{-i\frac{2\pi (N-1)}{N}k},k=N-1$

还是不够直观？举个离散数据的例子来看：

$x_0=1$
$x_1=2$
$x_3=3$
$x_4=4$
$X_0=x_0{e}^{-i\frac{2\pi 0}{N}k}+x_1{e}^{-i\frac{2\pi 1}{N}k}+\cdots +x_{N-1}{e}^{-i\frac{2\pi (N-1)}{N}k},k=0,N=4$
$X_1=x_0{e}^{-i\frac{2\pi 0}{N}k}+x_1{e}^{-i\frac{2\pi 1}{N}k}+\cdots +x_{N-1}{e}^{-i\frac{2\pi (N-1)}{N}k},k=1,N=4$
$X_2=x_0{e}^{-i\frac{2\pi 0}{N}k}+x_1{e}^{-i\frac{2\pi 1}{N}k}+\cdots +x_{N-1}{e}^{-i\frac{2\pi (N-1)}{N}k},k=2,N=4$
$X_3=x_0{e}^{-i\frac{2\pi 0}{N}k}+x_1{e}^{-i\frac{2\pi 1}{N}k}+\cdots +x_{N-1}{e}^{-i\frac{2\pi (N-1)}{N}k},k=3,N=4$

$X_0=1e^{-i\frac{2\pi 0}{4}0}+2e^{-i\frac{2\pi 1}{4}0}+3e^{-i\frac{2\pi (2)}{4}0}+4e^{-i\frac{2\pi (3)}{4}0}=10+0i$
$X_1=1e^{-i\frac{2\pi 0}{4}1}+2e^{-i\frac{2\pi 1}{4}1}+3e^{-i\frac{2\pi (2)}{4}1}+4e^{-i\frac{2\pi (3)}{4}1}=-2+2i$
$X_2=1e^{-i\frac{2\pi 0}{4}2}+2e^{-i\frac{2\pi 1}{4}2}+3e^{-i\frac{2\pi (2)}{4}2}+4e^{-i\frac{2\pi (3)}{4}2}=-2+0i$
$X_3=1e^{-i\frac{2\pi 0}{4}3}+2e^{-i\frac{2\pi 1}{4}3}+3e^{-i\frac{2\pi (2)}{4}3}+4e^{-i\frac{2\pi (3)}{4}3}=-2-2i$

令：$w=e^{\frac{-i2\pi }{N}}$
把这个案例写成矩阵的形式：
$\left[\begin{array}{c}{X}_0\\ X_1\\ X_2\\ X_3\end{array}\right]=\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& w& w^2& w^3\\ 1& w^2& w^4& w^6\\ 1& w^3& w^6& w^9\end{array}\right]\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ x_3\end{array}\right]$
完成这4个点DFT，需计算 16次乘法，即矩阵F中每个元素都会参与一次乘法，共 4个元素；12次加法，即每完成一个点需要3次加法。直到现在DFT终于高懂了，但是计算起来太麻烦了，效率太低。数据越大，计算量越大。FFT出现解决了计算量大的问题。

$w=e^{\frac{-i2\pi }{N}}$ 具有对称性，这是FFT简化的计算的方法，即：
$W_N^{k+\frac{N}{2}}=-W_N^k$

$X_k={\sum }_{n=0}^{N-1}{x}_n{e}^{-i\frac{2\pi n}{N}k}$

再写一遍，加深印象： $w=e^{\frac{-i2\pi }{N}}$

$X_k={\sum }_{n=0}^{N-1}{x}_n{w}^{nk}$

再看这个公式，变化即是信号值乘以对应的复数$e^{-i\frac{2\pi n}{N}k}$再求累加。
根据对称性可以简化傅里叶的计算，这就是FFT的意义。

分治法实现

上面的式子再写一遍，就当加深印象了，好累！！！！！

令：$w=e^{\frac{-i2\pi }{N}}$

$X_0=1e^{-i\frac{2\pi 0}{4}0}+2e^{-i\frac{2\pi 1}{4}0}+3e^{-i\frac{2\pi (2)}{4}0}+4e^{-i\frac{2\pi (3)}{4}0}=10+0i$
$X_1=1e^{-i\frac{2\pi 0}{4}1}+2e^{-i\frac{2\pi 1}{4}1}+3e^{-i\frac{2\pi (2)}{4}1}+4e^{-i\frac{2\pi (3)}{4}1}=-2+2i$
$X_2=1e^{-i\frac{2\pi 0}{4}2}+2e^{-i\frac{2\pi 1}{4}2}+3e^{-i\frac{2\pi (2)}{4}2}+4e^{-i\frac{2\pi (3)}{4}2}=-2+0i$
$X_3=1e^{-i\frac{2\pi 0}{4}3}+2e^{-i\frac{2\pi 1}{4}3}+3e^{-i\frac{2\pi (2)}{4}3}+4e^{-i\frac{2\pi (3)}{4}3}=-2-2i$

$X_0=w^{0\times 0}{x}_0+w^{1\times 0}{x}_1+w^{2\times 0}{x}_2+w^{3\times 0}{x}_3$
$X_1=w^{0\times 1}{x}_0+w^{1\times 1}{x}_1+w^{2\times 1}{x}_2+w^{3\times 1}{x}_3$
$X_2=w^{0\times 2}{x}_0+w^{1\times 2}{x}_1+w^{2\times 2}{x}_2+w^{3\times 2}{x}_3$
$X_3=w^{0\times 3}{x}_0+w^{1\times 3}{x}_1+w^{2\times 3}{x}_2+w^{3\times 3}{x}_3$

---

这样我们将上式分下组，接着讲，将奇数分为一组，偶数分为一组！！！！！！

---

$X_0=w^{0\times 0}{x}_0+w^{2\times 0}{x}_2+w^{1\times 0}{x}_1+w^{3\times 0}{x}_3$
$X_1=w^{0\times 1}{x}_0+w^{2\times 1}{x}_2+w^{1\times 1}{x}_1+w^{3\times 1}{x}_3$
$X_2=w^{0\times 2}{x}_0+w^{2\times 2}{x}_2+w^{1\times 2}{x}_1+w^{3\times 2}{x}_3$
$X_3=w^{0\times 3}{x}_0+w^{2\times 3}{x}_2+w^{1\times 3}{x}_1+w^{3\times 3}{x}_3$

$\left[\begin{array}{cccc}{w}^{0\times 0}& w^{2\times 0}& w^{1\times 0}& w^{3\times 0}\\ w^{0\times 1}& w^{2\times 1}& w^{1\times 1}& w^{3\times 1}\\ w^{0\times 2}& w^{2\times 2}& w^{1\times 2}& w^{3\times 2}\\ w^{0\times 3}& w^{2\times 3}& w^{1\times 3}& w^{3\times 3}\end{array}\right]\left[\begin{array}{c}{x}_0\\ x_2\\ x_1\\ x_3\end{array}\right]=\left[\begin{array}{cccc}{w}^0& w^0& w^0& w^0\\ w^0& w^2& w^1& w^3\\ w^0& w^4& w^2& w^6\\ w^0& w^6& w^3& w^9\end{array}\right]\left[\begin{array}{c}{x}_0\\ x_2\\ x_1\\ x_3\end{array}\right]$

$w=e^{\frac{-i2\pi }{N}}$
根最美公式欧拉公式：
$e^{ix}=\cos (x)+i\sin (x)$
上述的矩阵还可以写成：
$w^{n\times k}=\cos (\frac{2\pi }{N}\times n\times k)-i\sin (\frac{2\pi }{N}\times n\times k)$

$\left[\begin{array}{cccc}\cos (\frac{2\pi }{4}\times 0)-i\sin (\frac{2\pi }{4}\times 0)& \cos (\frac{2\pi }{4}\times 0)-i\sin (\frac{2\pi }{4}\times 0)& \cos (\frac{2\pi }{4}\times 0)-i\sin (\frac{2\pi }{4}\times 0)& \cos (\frac{2\pi }{N}\times 0)-i\sin (\frac{2\pi }{4}\times 0)\\ \cos (\frac{2\pi }{4}\times 0)-i\sin (\frac{2\pi }{4}\times 0)& \cos (\frac{2\pi }{4}\times 2)-i\sin (\frac{2\pi }{4}\times 2)& \cos (\frac{2\pi }{4}\times 1)-i\sin (\frac{2\pi }{4}\times 1)& \cos (\frac{2\pi }{N}\times 3)-i\sin (\frac{2\pi }{4}\times 3)\\ \cos (\frac{2\pi }{4}\times 0)-i\sin (\frac{2\pi }{4}\times 0)& \cos (\frac{2\pi }{4}\times 4)-i\sin (\frac{2\pi }{4}\times 4)& \cos (\frac{2\pi }{4}\times 2)-i\sin (\frac{2\pi }{4}\times 2)& \cos (\frac{2\pi }{N}\times 6)-i\sin (\frac{2\pi }{4}\times 6)\\ \cos (\frac{2\pi }{4}\times 0)-i\sin (\frac{2\pi }{4}\times 0)& \cos (\frac{2\pi }{4}\times 6)-i\sin (\frac{2\pi }{4}\times 6)& \cos (\frac{2\pi }{4}\times 3)-i\sin (\frac{2\pi }{4}\times 3)& \cos (\frac{2\pi }{N}\times 9)-i\sin (\frac{2\pi }{4}\times 9)\end{array}\right]\left[\begin{array}{c}{x}_0\\ x_2\\ x_1\\ x_3\end{array}\right]$

由于$w=e^{\frac{-i2\pi }{N}}$ 具有周期性，所以可以将w的幂次方简化，由于N=4。所以可以看成周期为4。
例如：
在N=4的条件下根据周期性可得以下结论：
根据周期性：
$w^4=1$
$w^9=w^1$
$w^6=w^2$
根据对称性：
$w^1=-w^3$
$w^0=-w^2$

证明：

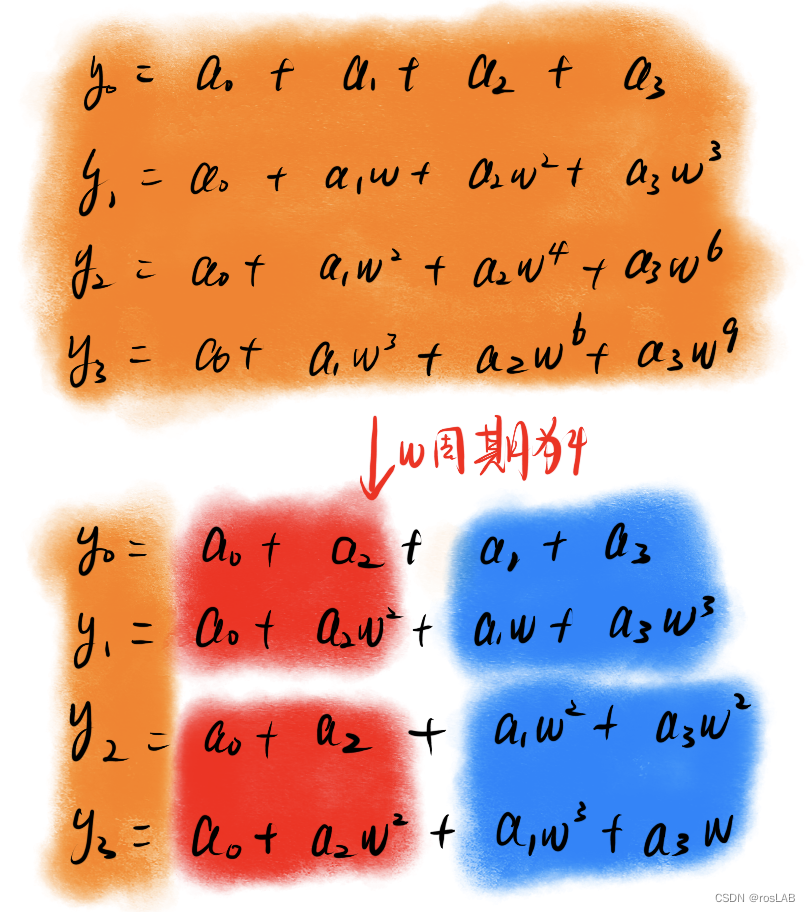
可以发现红色区域的内容相同，蓝色区域的内容相差一个${\omega }^2$ 因此我们只需要计算一半的内容即可。由于加法次数多于乘法，因此复杂度只需考虑加法使用的次数，本次计算耗时：2 （ 红 色 用 两 次 加 法 ） + 2 （ 蓝 色 用 两 次 加 法 ） + 4 （ 中 间 的 4 个 加 法 ） = 4 l o g 2 4 2（红色用两次加法）+ 2（蓝色用两次加法）+4（中间的4个加法）=$4{\log }_2(4)$

当n=8时

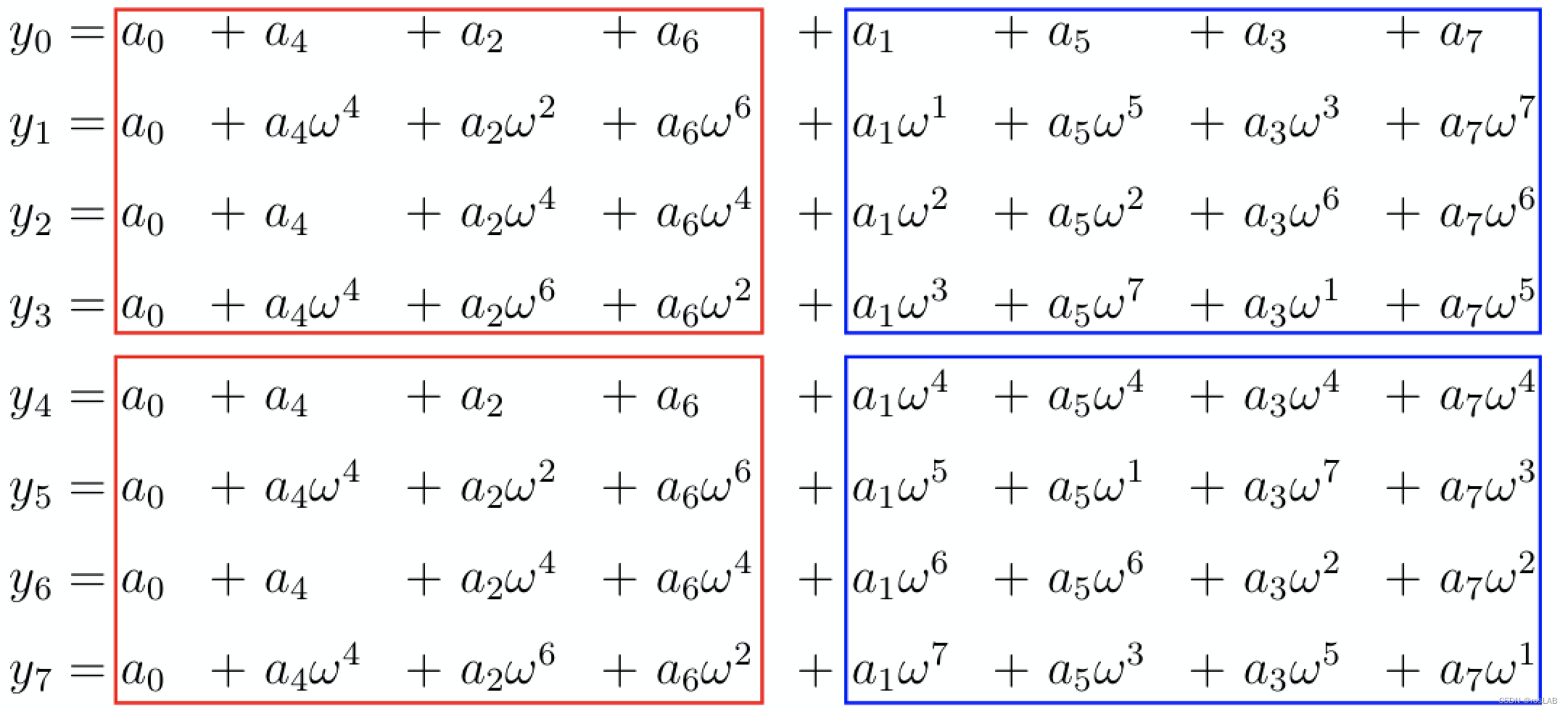
其中，绿色区域覆盖全部，表示开始需要计算的内容，棕色区域只包含了上半部分的两块内容，在得到棕色区域结果后可以顺势得到下半部分的绿色区域，橙色区域包含上面1/4部分的两块区域，红色区域则值包含最上面一行的两块区域。 绿(要求)->棕(要求)->橙(要求)->红(解)->橙(解)->棕(解)->绿(解)，这是一个很明显的递归过程。

FFT

IFFT

本身是一个求逆的过程，由于范德蒙矩阵的特性，得到结果如下

---

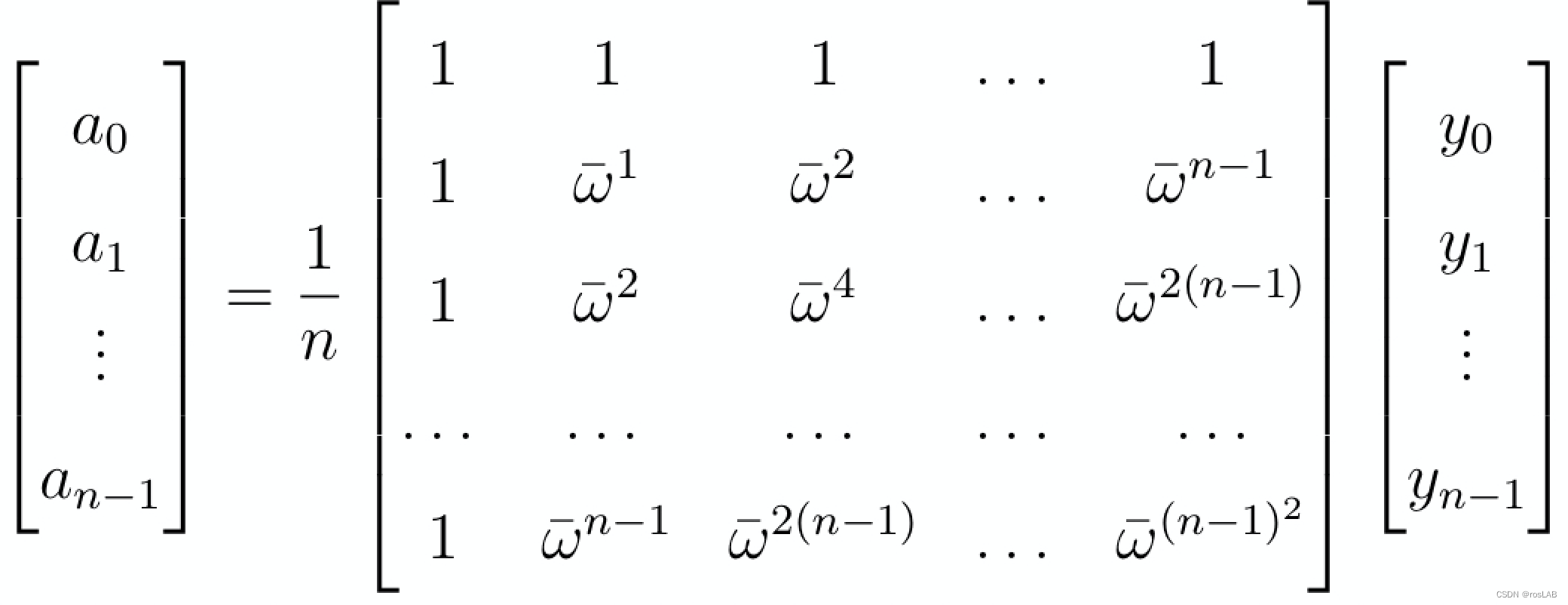
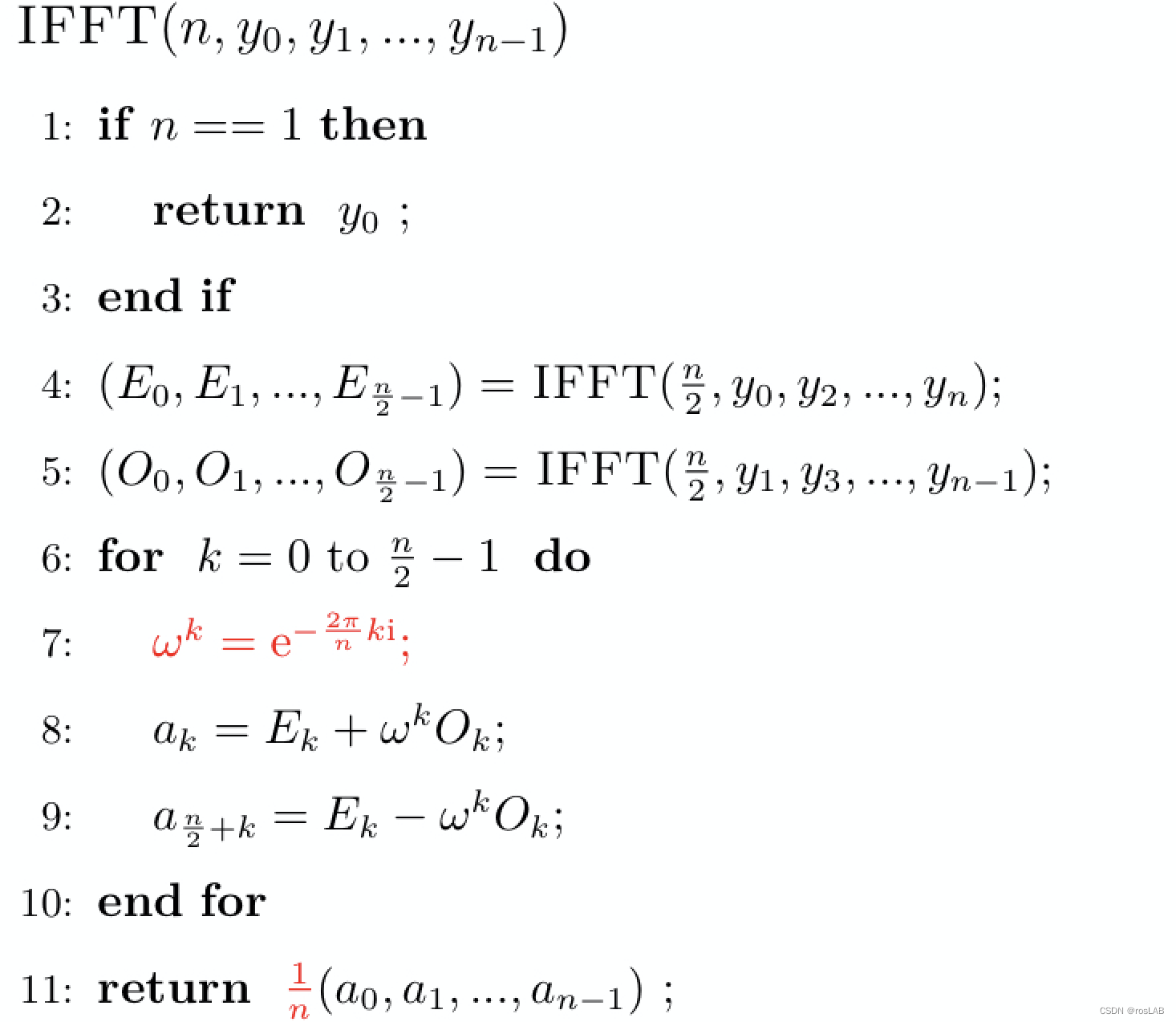
再写一遍：

$X_k={\sum }_{n=0}^{N-1}{x}_n{e}^{-i\frac{2\pi n}{N}k}，k=0,1,\dots ,N-1$
$X_k={\sum }_{n=0}^{N-1}x(n)\times \cos (\frac{2\pi n}{N}k)-i{\sum }_{n=0}^{N-1}x(n)\times \sin (\frac{2\pi n}{N}k)$

应用

等有时间再作整理……

C++代码实现

等有时间再作整理……