[Python嗯~机器学习]---对熵、条件熵、相对熵的补充

版权声明：允许转载请注明作者 https://blog.csdn.net/kepengs/article/details/86627810

熵、条件熵、相对熵、交叉熵

熵

首先，我们可以理解熵是一个量化信息量的东西，用来度量信息的多少。一件事情的信息量和不确定性是有关系的，信息量越大就表示不确定性越大。举一个例子：中国运动员将在2020年东京奥运会赢得短跑冠军。这个例子中，因为大家都知道几乎是不可能的，所以就不需要去查阅和引入很多信息，信息量就很少，熵就很小。反之，亦然。

这时候，我们把上面的例子泛化成一个事件 ，那么  发生的概率越大，它的信息熵越小。也就是要找 。

我们用一个函数来表示信息量 。那么信息量  和事件  发生的概率  之间就会产生某种联系。。两个事件如果相互之间没有任何关系，那么这两个事件  和  同时发生的信息量为 ，并且同时发生的概率为 。

通过对数公式  和两个事件同时发生的信息量和概率的公式可以看出信息量  和概率  之间是对数关系。

所以，可以表示成 ，因为概率是  之间的数， 为负数，通过前面加一个负号把整体移动到  轴上方。

就是自信息，描述某一个事件  发生所带来的信息量。

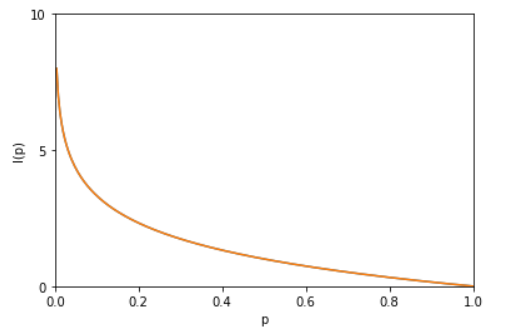
从上图也可以看出，当一个事件确定发生的时候，其信息量为 0 。

这时候我们开始讨论信息熵，还是举一个例子：假设 A 向 B 传输关于变量  的值，那么传输的平均信息量就可以通过信息量公式  对概率密度  求期望：

其中， 就被称为随机变量  的熵,它是表示随机事件不确定的度量，是对所有可能发生的事件产生的信息量的期望。
从上式，可以看出随机变量  越多，状态数就越多，不确定性就越大，熵就越大。均匀分布熵最大。

联合熵

将一维的随机变量分布推广到高维，就叫做联合熵。

证明均匀分布熵最大

还是举一个例子，假设随机变量  具有某一个值，但是传输过程中有四种状态， 假设所有状态都是等可能的话，根据熵的公式可以得出我们需要传播的信息量为

假设四种状态有不同的概率为 ，那么信息量为

通过上面的例子得出均匀分布的熵最大。这样，我们就可以用哈夫曼编码来代表概率，用短编码代表概率高的事件，用长编码代表概率低的事件。
熵是传输一个随机变量状态值所需的比特位下界（最短平均编码长度），所以可以用来做数据压缩。

证明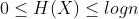

拉格朗日乘子法：
因为 
所以，
目标函数
约束条件 

1、定义拉格朗日函数：

2、 分别对  求偏导数，令偏导数等于 0，

3、求出  的值，
解方程 ，代入  得到目标函数极值：

证明，  为最大值。

条件熵

条件熵  表示在已知随机变量  的条件下随机变量  的不确定性。条件熵  定义为  给定条件下  的条件概率分布的熵对  的数学期望：

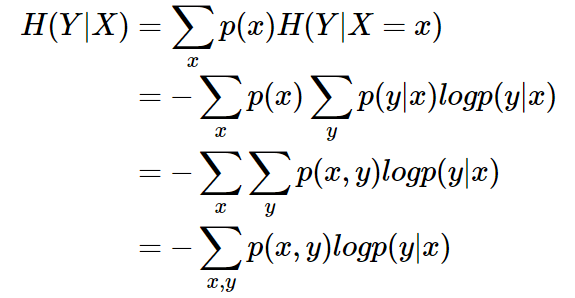
条件熵  相当于联合熵  减去单独的熵 ，即，证明如下：

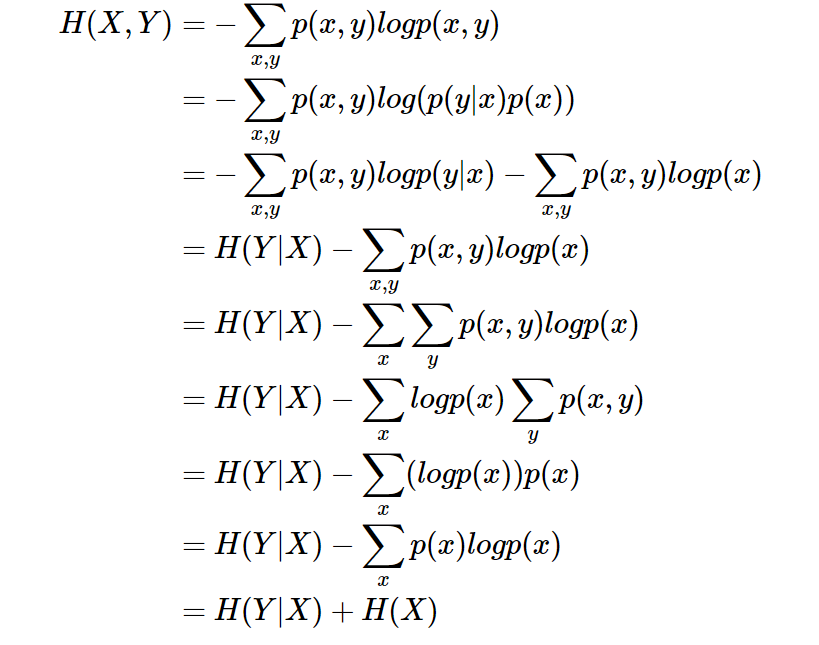
还是举个例子，温度高低和穿短袖长袖是有关系的，所以这两个事件的联合熵就可以写成，两个事件的信息量肯定是大于单一事件的信息量的，假设  表示今天环境温度的信息量，由于今天环境温度和今天我穿什么衣服这两个事件并不是独立分布的，所以在已知今天环境温度的情况下，我穿什么衣服的信息量或者说不确定性是被减少了。当已知  这个信息量的时候， 剩下的信息量就是条件熵：

描述  和  所需的信息是描述  自己所需的信息,加上给定   的条件下具体化   所需的额外信息。

相对熵，KL散度

设 、 是 离散随机变量  中取值的两个概率分布，则  对  的相对熵是：

性质：

1、如果  和  两个分布相同，那么相对熵等于0
2、，相对熵具有不对称性。大家可以举个简单例子算一下。
3、 证明如下（利用Jensen不等式）：

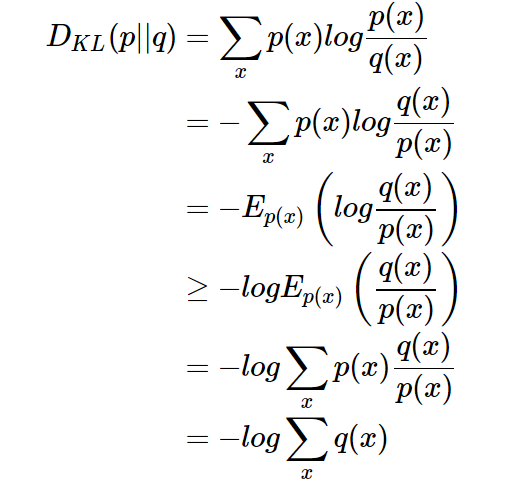
因为，所以有。
总结：相对熵可以用来衡量两个概率分布之间的差异，上面公式的意义就是求  与 之间的对数差在  上的期望值。

交叉熵

现在有关于样本集的两个概率分布  和 ，其中   为真实分布，  非真实分布。如果用真实分布  来衡量识别别一个样本所需要编码长度的期望（平均编码长度）为:

如果使用非真实分布  来表示来自真实分布 的平均编码长度，则是：

（因为用  来编码的样本来自于分布  ，所以  中的概率是 ）。此时就将  称之为交叉熵。
还是举一个例子。考虑一个随机变量 ，真实分布，非真实分布 ， 则（最短平均码长），交叉熵 。由此可以看出根据非真实分布  得到的平均码长大于根据真实分布  得到的平均码长。

我化简一下相对熵的公式：

这时候对比一下熵和交叉熵公式：
熵：
交叉熵：
推出：

（当用非真实分布  得到的平均码长比真实分布  得到的平均码长多出的比特数就是相对熵）
又因为相对熵 。
所以 （当  时取等号，此时交叉熵等于信息熵，相对熵等于 0）

并且当  为常量时（注：在机器学习中，训练数据分布是固定的），最小化相对熵  等价于最小化交叉熵  也等价于最大化似然估计。

在机器学习中，我们希望在训练数据上模型学到的分布  和真实数据的分布   越接近越好，所以我们可以使其相对熵最小。但是我们没有真实数据的分布，所以只能希望模型学到的分布 和训练数据的分布  尽量相同。假设训练数据是从总体中独立同分布采样的，那么我们可以通过最小化训练数据的经验误差来降低模型的泛化误差。即：

1. 希望学到的模型的分布和真实分布一致，
2. 但是真实分布不可知，假设训练数据是从真实数据中独立同分布采样的，
3. 因此，我们希望学到的模型分布至少和训练数据的分布一致，

根据之前的描述，最小化训练数据上的分布   与最小化模型分布  的差异等价于最小化相对熵，即。此时，  就是  中的 ，即真实分布， 就是 。又因为训练数据的分布  是给定的，所以求    等价于求 。得证，交叉熵可以用来计算学习模型分布与训练分布之间的差异。交叉熵广泛用于逻辑回归的Sigmoid和Softmax函数中作为损失函数使用。

总结

5、总结

1. 信息熵是衡量随机变量分布的混乱程度，是随机分布各事件发生的信息量的期望值，随机变量的取值个数越多，状态数也就越多，信息熵就越大，混乱程度就越大。当随机分布为均匀分布时，熵最大；信息熵推广到多维领域，则可得到联合信息熵；条件熵表示的是在  给定条件下， 的条件概率分布的熵对  的期望。
2. 相对熵可以用来衡量两个概率分布之间的差异。
3. 交叉熵可以来衡量在给定的真实分布下，使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。

或者：

1. 信息熵是传输一个随机变量状态值所需的比特位下界（最短平均编码长度）。
2. 相对熵是指用  来表示分布   额外需要的编码长度。
3. 交叉熵是指用分布  来表示本来表示分布  的平均编码长度。

通常“相对熵”也可称为“交叉熵”，因为真实分布  是固定的， 由  决定。当然也有特殊情况，彼时2者须区别对待。