机器学习 - 香农信息量，熵，联合熵，条件熵，相对熵，交叉熵，互信息

1. 香农信息量

1.1 引子

假设我们听到了两件事，分别如下：
事件A：我今天收到了乔治城大学的录取。
事件B：我今天收到了哈佛的录取。
仅凭直觉来说，显而易见事件B的信息量比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

如果是连续型随机变量的情况，设p为随机变量X的概率分布，即p(x)为随机变量X在X = x处的概率密度函数值，则随机变量X在X = x处的香农信息量定义为：
$$-lo{g}_{2}p(x)$$

这时香农信息量的单位为比特。由香农信息量我们可以知道对于一个已知概率的事件，我们需要多少的数据量能完整地把它表达清楚，不与外界产生歧义。

1.2 举例

假设我们有一段数据长下面这样：aaBaaaVaaaaa

可以算出三个字母出现的概率分别为：

a : 10/12 ， B : 1/12 ， V : 1/12

香农信息量为：a : 0.263 ， B : 3.585 ， V : 3.585

也就是说如果我们要用比特来表述这几个字母，分别需要0.263 ， 3.585 ， 3.585个这样的比特。当然，由于比特是整数的，因此应该向上取整，变为1,4,4个比特。

这个时候我们就可以按照这个指导对字母进行编码，比如把a编码为"0"，把B编码为"1000"，V 编码为"1001"，然后用编码替换掉字母来完成压缩编码，数据压缩结果为：001000000100100000.

2.熵

对于整个系统而言，我们更加关心的是表达系统整体所需要的信息量。比如我们上面举例的aaBaaaVaaaaa这段字母，虽然B和V的香农信息量比较大，但他们出现的次数明显要比a少很多，因此我们需要有一个方法来评估整体系统的信息量。
很自然地想到利用期望，因此评估的方法可以是：“事件香农信息量×事件概率”的累加。这也正是信息熵的概念。
$$H(p)=\sum _{i=1}^{n}p(X=x_i)lo{g}_{2}p(X=x_i)$$

信息熵衡量了系统的混乱程度，如果k个事件都是等概率发生，那么混乱程度最大，信息熵也最大。

3.联合熵

两个随机变量X，Y的联合分布，可以形成联合熵，用H(X,Y)表示。
$$H(X,Y)=\sum _{i,j}p(X=x_i,Y=y_j)lo{g}_{2}p(X=x_i,Y=y_j)$$

4. 条件熵

【定义1】条件熵
在随机变量Y发生的前提下，随机变量X的信息熵。用来衡量在已知随机变量Y的条件下随机变量X的不确定性。
$$\begin{gathered} H(X|Y)=\sum _{j}P(Y=y_j)H(X|Y=y_j) \\ =\sum _{j}P(Y=y_j)\sum _{i}P(X=x_i|Y=y_j)lo{g}_{2}P(X=x_i|Y=y_j) \\ =\sum _{i,j}P(y_j)P(x_i|y_j)lo{g}_{2}P(x_i|y_j) \\ =\sum _{i,j}P(x_i,y_j)lo{g}_{2}P(x_i|y_j) \end{gathered}$$

【性质】
$$H(X\mid Y)=H(X,Y)-H(Y)$$
推导：
$$\begin{gathered} H(X|Y)=\sum _{i,j}P(x_i,y_j)lo{g}_{2}P(x_i|y_j) \\ =\sum _{i,j}P(x_i,y_j)lo{g}_2\frac{P(x_i,y_j)}{P(y_j)} \\ =\sum _{i,j}P(x_i,y_j)[lo{g}_{2}P(x_i,y_j)-lo{g}_{2}P(y_j)] \\ =H(X,Y)-H(Y) \end{gathered}$$

5. 相对熵(KL散度)

5.1 直观解释

KL 散度是一种衡量两个分布之间的匹配程度的方法。

5.2 一个有趣的例子

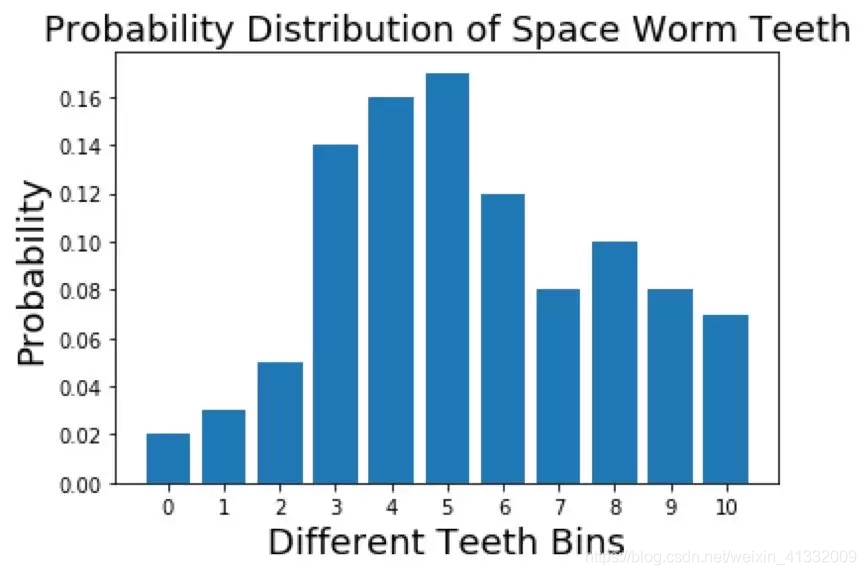
假设我们是一组正在广袤无垠的太空中进行研究的科学家。我们发现了一些太空蠕虫，这些太空蠕虫的牙齿数量各不相同。现在我们需要将这些信息发回地球。但从太空向地球发送信息的成本很高，所以我们需要用尽量少的数据表达这些信息。我们有个好方法：我们不发送单个数值，而是绘制一张图表，其中 X 轴表示所观察到的不同牙齿数量（0,1,2…），Y 轴是看到的太空蠕虫具有 x 颗牙齿的概率（即具有 x 颗牙齿的蠕虫数量/蠕虫总数量）。这样，我们就将观察结果转换成了分布。

发送分布比发送每只蠕虫的信息更高效。但我们还能进一步压缩数据大小。我们可以用一个已知的分布来表示这个分布（比如均匀分布、二项分布、正态分布）。举个例子，假如我们用均匀分布来表示真实分布，我们只需要发送两段数据就能恢复真实数据：均匀概率和蠕虫数量。但我们怎样才能知道哪种分布能更好地解释真实分布呢？这就是 KL 散度的用武之地。

假设有 100 只蠕虫，各种牙齿数的蠕虫的数量统计结果如下。
0 颗牙齿：2（概率：p_0 = 0.02）
1 颗牙齿：3（概率：p_1 = 0.03）
2 颗牙齿：5（概率：p_2 = 0.05）
3 颗牙齿：14（概率：p_3 = 0.14
4 颗牙齿：16（概率：p_4 = 0.16）
5 颗牙齿：15（概率：p_5 = 0.15）
6 颗牙齿：12（概率：p_6 = 0.12）
7 颗牙齿：8（概率：p_7 = 0.08）
8 颗牙齿：10（概率：p_8 = 0.1）
9 颗牙齿：8（概率：p_9 = 0.08）
10 颗牙齿：7（概率：p_10 = 0.07）

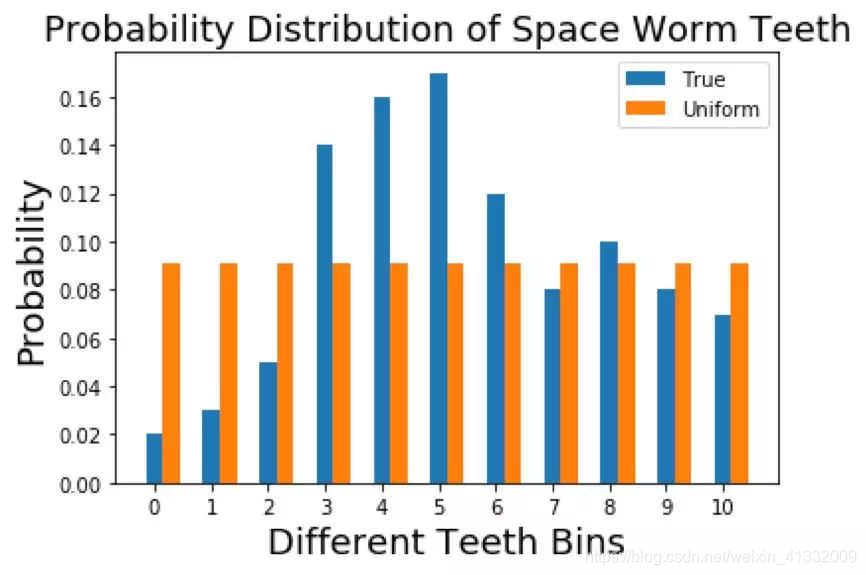
尝试1 :使用均匀分布建模

我们首先使用均匀分布来建模该分布。均匀分布只有一个参数：均匀概率；即给定事件发生的概率。
$$p_{uniform}=\frac{1}{11}=0.0909$$
均匀分布和真实分布对比：

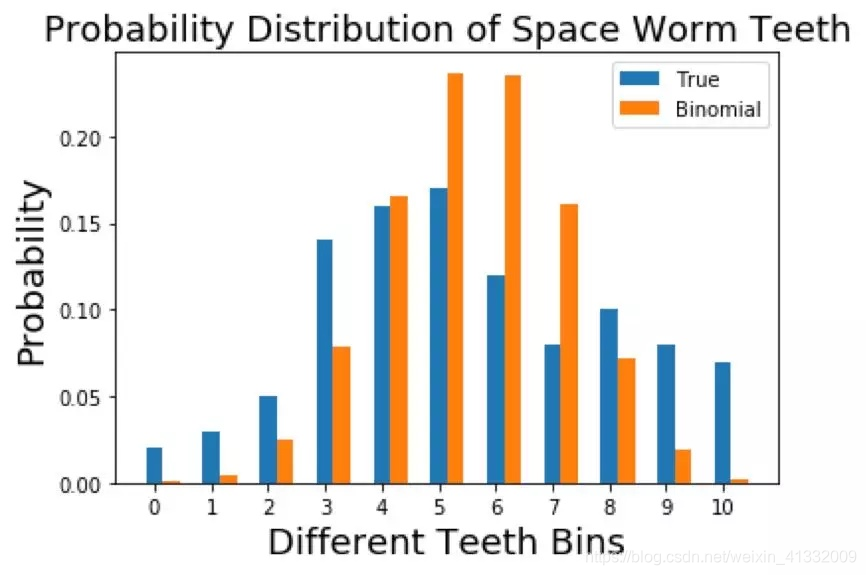
尝试2：使用二项分布建模

由于二项分布的均值为$np$，方差为$np(1-p)$,经计算得到p=0.544.
二项分布和真实分布对比：

我们如何定量地确定哪个分布更好？
经过这些计算之后，我们需要一种衡量每个近似分布与真实分布之间匹配程度的方法。这很重要，这样当我们发送信息时，我们才无需担忧「我是否选择对了？」毕竟太空蠕虫关乎我们每个人的生命。
这就是 KL 散度的用武之地。

【定义2】
KL散度在形式上定义如下：
$$D_{KL}(p||q)=\sum _{i=1}^{n}p(X=x_i)log\frac{p(X=x_i)}{q(X=x_i)}$$
其中 q(x) 是近似分布，p(x) 是真实分布。直观地说，这衡量的是给定任意分布偏离真实分布的程度。如果两个分布完全匹配，那么 $D_{KL}(p||q)=0$

KL 散度越小，真实分布与近似分布之间的匹配就越好。

5.3 公式的直观解释

让我们看看 KL 散度各个部分的含义。首先看看
$log\frac{p(X=x_i)}{q(X=x_i)}$项，如果 $q(X=x_i)$ 大于 $p(X=x_i)$ , 这个项的值为负。另一方面，如果 $q(X=x_i)$总是小于 $p(X=x_i)$，那么该项的值为正。如果 $q(X=x_i)==p(X=x_i)$则该项的值为 0。然后，为了使这个值为期望值，你要用 $p(X=x_i)$ 来给这个对数项加权。也就是说，$p(X=x_i)$ 有更高概率的匹配区域比低 $p(X=x_i)$ 概率的匹配区域更加重要。

5.4 性质

1）不对称性

尽管KL散度从直观上是个度量或距离函数，但它并不是一个真正的度量或者距离，因为它不具有对称性，即D(P||Q)!=D(Q||P)。这是因为KL散度是针对近似分布偏离真实分布的程度来说的。

（2）非负性

相对熵的值是非负值，即D(P||Q)>0。

6.交叉熵

6.1 和KL散度的关系

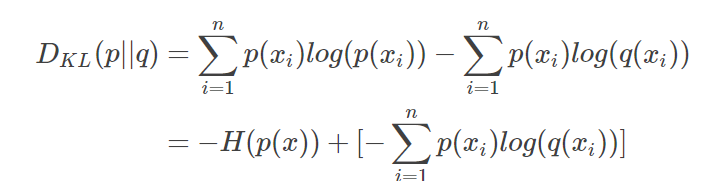
等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：

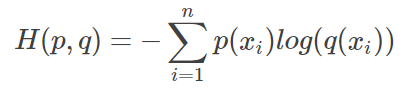
其中，$p(x_i)$是真实分布，$q(x_i)$是预测分布。

在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即$D_{KL}(y||\hat{y})$，由于KL散度中的前一部分$-H(y)$不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用交叉熵做loss，评估模型。

6.2 举例

单分类问题：

$$loss=-(0\times log(0.3)+1\times log(0.6)+0\times log(0.1)=log(0.6)$$
多分类问题：

这里不采用softmax(因为概率总和不再是1)，而是采用sigmoid把每个概率值放缩到(0,1)即可。

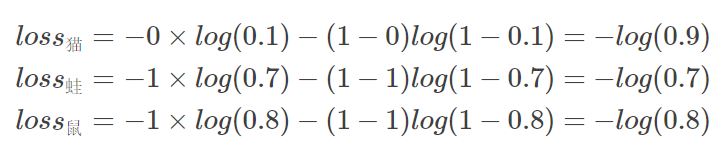
单个样本的loss即为$$loss=los{s}_{猫}+los{s}_{蛙}+los{s}_{鼠}$$

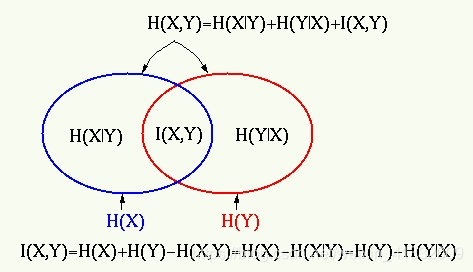
7. 互信息

7.1 启发式定义

Mutual Information表示两个变量X与Y是否有关系，以及关系的强弱。形象的解释是：假如X是一个随机事件，Y也是一个随机事件，那么X和Y相互依赖的程度应该是：
不知道X时，Y发生的不确定性（熵）- 已知X时，Y发生的不确定性(熵)。即：

$$I(X;Y)=H(Y)-H(Y|X)=H(X)-H(X|Y)$$

公式

熵和条件熵：

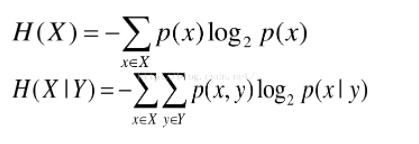
互信息：从概率角度，互信息是由随机变量X、Y的联合概率分布 p(x,y)和边缘概率分布 p(x), p(y)得出。

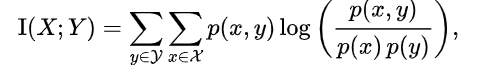
互信息和熵的关系是：