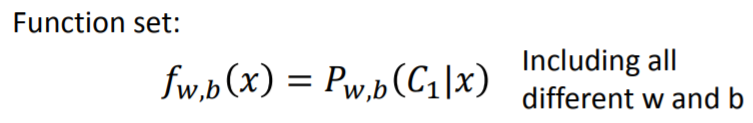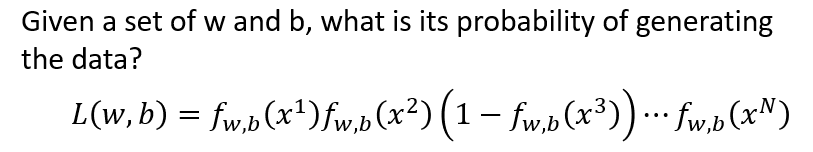ML Lecture 5: Classification——Logistic Regression
Logistic回归
在前面用概率生成模型解决分类问题的基础上,本节继续介绍判别模型——Logistic回归解决分类问题。按照机器学习三个步骤(确定模型/函数集、判断函数优劣、寻找最佳函数),介绍Logistic回归的基本原理。
1. 确定模型/函数集
在二分类问题中,我们的模型/函数集其实就是后验概率
P(C1|x)
。分类的判断依据是:
- 若
P(C1|x)>0.5
,样本
x
就属于第一类
- 若
P(C1|x)<0.5
,样本
x
就属于第二类

后验概率
P(C1|x)
可以化为Sigmoid函数
σ(z)
, 而
z=wTx+b=∑kwkxk+b
。
其中,样本
x
共有
K
维特征,则
w
和
x
都是
K
维向量,
wTx
是两个向量的内积。
b
是一个常数,称为偏置(Bias)。
xk
表示样本
x
的第
k
维特征(
k=1,2,..,K
),
wk
是样本
x
第
k
维特征的权重(Weight)。模型与各参数之间的关系用图形表示为:
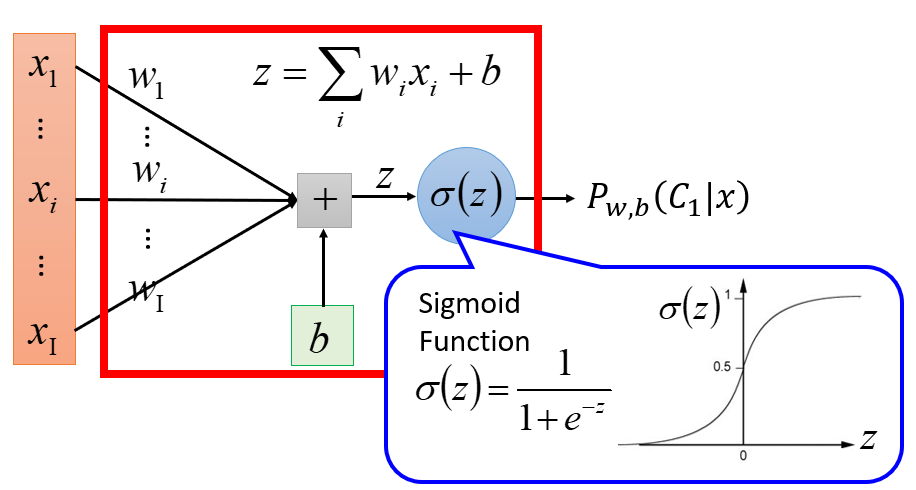
所以,
P(C1|x)
是由
K
维向量
w
和常数
b
决定的模型/函数集。选择不同的
w
和
b
,就会得到不同的函数。
将
P(C1|x)
、
σ(z)
记为关于参数
w
和
b
的形式:
fw,b(x)=Pw,b(C1|x)=11+e−z=σ(z)=σ(wTx+b)=σ(∑kwkxk+b)
这个模型就称为
Logistic回归模型。
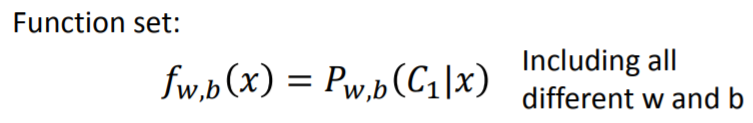
【Logistic回归 vs. 线性回归】
在机器学习第一个步骤——确定模型,Logistic回归和线性回归的区别在于:
- Logistic回归把每一个特征
xk
乘上对应的权重
wk
,加上常数
b
,再输入Sigmoid函数里。由于经过了Sigmoid函数的转换,所以Logistic回归输出的数值介于
[0,1]
之间
- 线性回归则是直接把每一个特征
xk
乘上对应的权重
wk
,加上常数
b
,而没有通过Sigmoid函数。所以线性回归输出的数值是任意的,在
[−∞,+∞]
之间

2. 判断函数优劣
依旧是二分类问题,假设
N
个训练样本
{x1,x2,x3,...,xN}
分别属于
{C1,C1,C2,...,C1}
类,它们是根据后验分布的模型
Pw,b(C1|x)
产生的。

给定一组参数
w′
和
b′
,也就相应确定了一个函数
fw′,b′(x)=Pw′,b′(C1|x)
。从而能够计算由
w′
和
b′
构成的函数
fw′,b′(x)
生成这
N
个样本的概率。
注意,
fw′,b′(x)
表示一个样本
x
来自
C1
的概率。所以,从
fw′,b′(x)
中产生
N
个样本的似然函数写为:
L(w′,b′)=fw′,b′(x1)⋅fw′,b′(x2)⋅(1−fw′,b′(x3))...fw′,b′(xN)
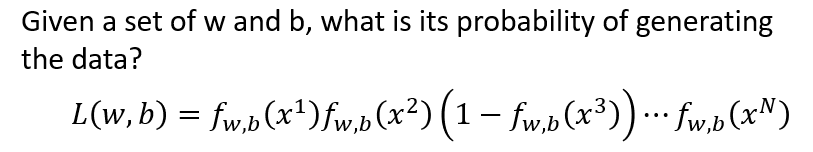
我们要做的是,穷尽所有可能的
w
和
b
,找到一组参数
w∗
和
b∗
,使得上面的似然函数最大。即找到使
N
个样本出现概率最大的那个函数:
(w∗,b∗)=argmaxw,bL(w,b)

如何通过一些简单的变换,找到最优的参数
w∗
和
b∗
?
似然函数
→
对数似然函数,最大化
→
最小化
对于似然函数:
L(w,b)=fw,b(x1)⋅fw,b(x2)⋅(1−fw,b(x3))...fw,b(xN)
由于它带有连乘结构,所以考虑用
log(x)
函数将其变成连加结构。而函数
log(x)
具有与
x
同增同减的特性,问题可以进一步转化为:
argmaxw,bL(w,b)→argmaxw,blnL(w,b)→argminw,b[−lnL(w,b)]
以上三个优化问题求得的
w∗
与
b∗
是相同的,但从求解问题一转化到求解问题三,计算更简便。

对数似然函数的新形式:引入交叉熵
H(p,q)=Ep[−logq]=−∑xp(x)logq(x)
最优参数的求解问题转变为
argminw,b[−lnL(w,b)]
后,
−lnL(w,b)
就是我们定义的用来判断函数优劣的损失函数(似然函数最大化
→
损失函数最小化):
−lnL(w,b)=−lnfw,b(x1)−lnfw,b(x2)−ln(1−fw,b(x3))−...−lnfw,b(xN)
由于不同类别的表达式不一样,第一类样本的形式是
−∑lnfw,b(xn)
,而第二类样本的形式是
−∑ln(1−fw,b(xn))
,无法将整个式子统一成
∑
形式(这里仅考虑二分类问题)。 所以考虑引入二分类变量
y^
。若第
n
个样本
xn
属于
C1
,对应的目标输出是
y^n=1
;若
xn
属于
C2
,对应的目标输出是
y^n=0
。所以,
y^n
即第
n
个样本
xn
的真实类别标签:
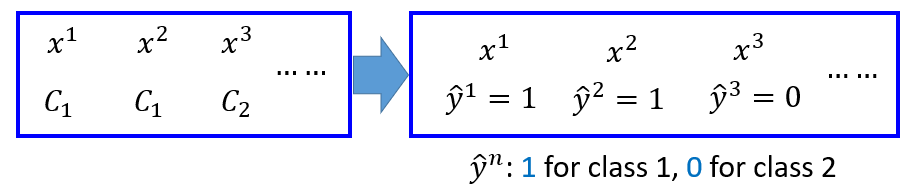
y^n={10,xn∈C1,xn∈C2
这个做法类似于线性回归中,每一个输入样本
x
都对应一个真实输出值
y^
。二者的区别在于,线性回归的
y^
可以是任意数值,而二分类问题的真实输出是某个类别,
y^
只能是
0
或
1
。
则
−lnL(w,b)
中的每一项都可以写为(省略函数
f
的下标参数
w
和
b
):
−[y^n⋅lnf(xn)+(1−y^n)⋅ln(1−f(xn))]

其中,
n=1,..,N
。显然:
- 当
xn∈C1
,
y^n=1
,上式等于
−lnf(xn)
- 当
xn∈C2
,
y^n=0
,上式等于
−ln(1−f(xn))
从而
−lnL(w,b)
就可以统一成
∑
的形式:
−lnL(w,b)=∑n=1N−[y^n⋅lnf(xn)+(1−y^n)⋅ln(1−f(xn))]
其中,
−[y^n⋅lnf(xn)+(1−y^n)⋅ln(1−f(xn))]
这一项是伯努利分布
X
~
B(1,y^n)
和伯努利分布
X
~
B(1,f(xn))
之间的交叉熵(Cross Entropy),是第
n
个样本
xn
的交叉熵。注意,
∑Nn=1
代表
N
个样本的交叉熵累加。

对于离散分布
p
、
q
,它们在给定样本集
{x1,x2,x3,...,xN}
上的交叉熵定义如下:
H(p,q)=Ep[−logq]=−∑xp(x)logq(x)
注意,这里的
∑x
表示样本
x
遍历所有可能的类别。
特别地,在Logistic回归(二分类问题)中,第
n
个样本
xn
只可能属于两个类别的其中一个,则
xn
的交叉熵展开写为:
H(p,q)=−[p(xn∈C1)logq(xn∈C1)+p(xn∈C2)logq(xn∈C2)]
p
、
q
是两个不同的伯努利分布(0-1分布、两点分布),其中:
p
为第
n
个样本
xn
的真实分布,服从参数为
y^n
的
0−1
分布,即
X
~
B(1,y^n)
p(xn∈C1)=y^n
p(xn∈C2)=1−y^n
【注】:真实分布是固定的
q
为第
n
个样本
xn
的估计分布,服从参数为
f(xn)
的
0−1
分布,即
X
~
B(1,f(xn))
q(xn∈C1)=f(xn)
q(xn∈C2)=1−f(xn)
代入上式,真实分布与估计分布的交叉熵写为:
H(p,q)=−[y^n⋅lnf(xn)+(1−y^n)⋅ln(1−f(xn))]

交叉熵反映的是分布
p
、
q
之间的相似程度。交叉熵有两个特性使得它能够作为Logistic回归的代价函数:
- 交叉熵是非负的。
y^n
的值等于
0
或
1
,而
f(xn)
的值介于
0
到
1
之间,
log
之后得负。整个式子前面添加了一个负号,所以交叉熵的数值非负
-
p
、
q
两个分布越相近,交叉熵越小。如果两个分布完全一样,计算出来的交叉熵就是
0
。例如:
当
xn∈C1
,
y^n=1
,若
f(xn)≈1
,则
H(p,q)≈0
当
xn∈C2
,
y^n=0
,若
f(xn)≈0
,则
H(p,q)≈0
事实上,均方代价函数也同时满足这两个特征。但交叉熵有另外一个特征是均方代价函数不具备的,就是交叉熵能够避免学习速率降低的情况,后详。
【Logistic回归 vs. 线性回归】
在机器学习第二个步骤——评价函数的优劣,Logistic回归和线性回归的区别在于:
Logistic回归中,评价一个函数优劣的方式是这样的:
对于训练集中的第
n
个样本
xn
,它对应一个真实类别的输出
y^n
。若
xn∈C1
,
y^n=1
;若
xn∈C2
,
y^n=0
。从而构成了样本对
(xn,y^n)
。这里,定义
y^n
的取值只能为
0
或
1
。
我们定义的损失函数(即需要最小化的对象),是所有样本的交叉熵总和:
L(f)=∑n=1NH(y^n,f(xn))=∑n=1N−[y^n⋅lnf(xn)+(1−y^n)⋅ln(1−f(xn))]
直观而言,我们希望找到一个函数
f(xn)
,它的输出能够与样本真实类别的输出
y^n
越接近越好。或者说,我们希望找到的伯努利分布与样本实际的伯努利分布越接近越好。线性回归的损失函数是均方误差(MSE):
L(f)=1N∑n=1N(f(xn)−y^n)2

3. 寻找最佳函数
根据第1步的变换:
fw,b(x)=Pw,b(C1|x)=11+e−z=σ(z)=σ(wTx+b)=σ(∑kwkxk+b)
第2步定义的损失函数:
L(f)=−lnL(w,b)
=∑n=1N−[y^n⋅lnfw,b(xn)+(1−y^n)⋅ln(1−fw,b(xn))]
=∑n=1N−[y^n⋅lnσ(zn)+(1−y^n)⋅ln(1−σ(zn))]
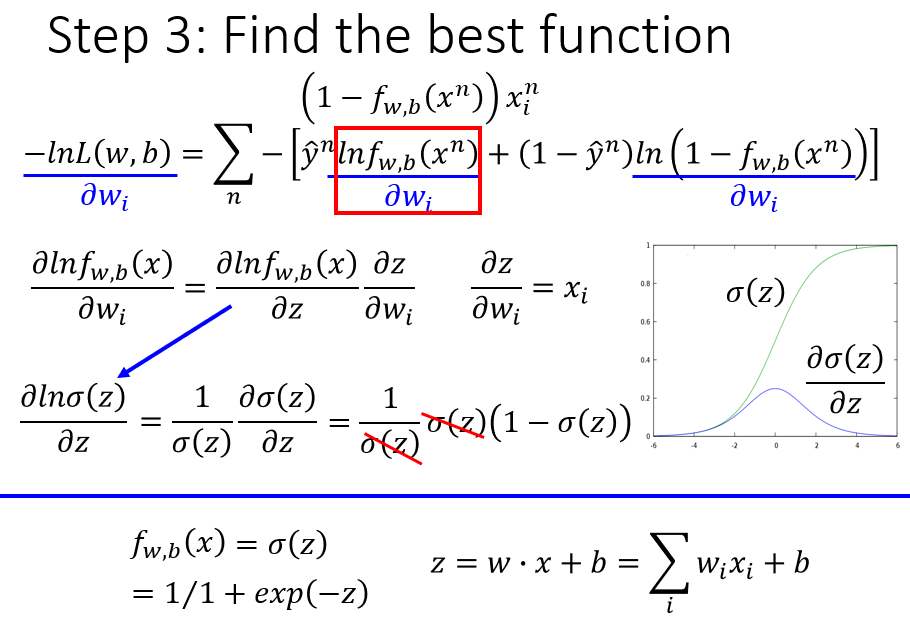
在第3步中,利用梯度下降法,求损失函数对权重
wk
的偏导:
∂L∂wk=∑n=1N−[y^n⋅∂lnσ(zn)∂wk+(1−y^n)⋅∂ln(1−σ(zn))∂wk]
=∑n=1N−[y^n⋅∂lnσ(zn)∂zn∂zn∂wk+(1−y^n)⋅∂ln(1−σ(zn))∂zn∂zn∂wk]
=∑n=1N−[y^n⋅σ′(zn)σ(zn)∂zn∂wk+(1−y^n)⋅−σ′(zn)1−σ(zn)∂zn∂wk]
=∑n=1N−[y^n⋅σ′(zn)σ(zn)−(1−y^n)⋅σ′(zn)1−σ(zn)]∂zn∂wk
其中,
∂zn∂wk=xnk
,
σ′(zn)=σ(zn)(1−σ(zn))
。
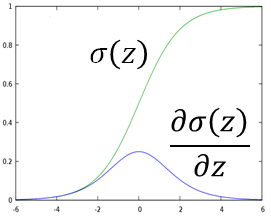
若在同一坐标图上画出
σ(z)
和
σ′(z)
的形状:由于
σ(z)
左右两端变化慢,中间段斜率很大,所以
σ′(z)
的两端趋近于
0
,在中间位置达到最大值,如下图。
将
∂zn∂wk
、
σ′(zn)
代入上式,则损失函数
L
对权重参数
wk
的偏导数可以化简为:
∂L∂wk=∑n=1N−[y^n⋅(1−σ(zn))−(1−y^n)⋅σ(zn)]xnk
=∑n=1N−[y^n−σ(zn)]xnk=∑n=1N−[y^n−fw,b(xn)]xnk


按照梯度下降法,将参数
wk
从第
g
个更新到第
g+1
个,其迭代公式为:
w(g+1)k=w(g)k−η∂L∂wk=w(g)k+η∑n=1N[y^n−fw,b(xn)]xnk
注意到,
wk
的更新取决于三个因素:
- 学习率
η
,是主观调整的
- 第
n
个样本的第
k
个特征值
xnk
,取决于样本数据
-
[y^n−fw,b(xn)]
,这一项代表模型的预测分布
fw,b(xn)
与真实分布
y^n
的差距有多大。假如
fw,b(xn)
距离真实分布还很远,亦即预测误差还很大,那么整体更新步伐就应该设大一点,这一参数更新理念也符合逻辑
【Logistic回归 vs. 线性回归】
在机器学习第三个步骤——寻找最佳函数/参数,Logistic回归和线性回归更新参数的方式是一样的,唯一不同的是数值输出:
- Logistic回归中,
y^n
的取值只能是
0
或
1
,
fw,b(xn)
是一个介于
[0,1]
之间的概率值
- 线性回归中,真实值
y^n
和预测值
fw,b(xn)
可以是任意实数

Logistic回归的损失函数:交叉熵还是平均误差?
为什么Logistic回归的损失函数要取交叉熵,而不按照线性回归那样直接取平方误差?如果Logistic回归的损失函数取平方误差会造成什么问题?
假设Logistic回归的损失函数取平方误差,则损失函数写为:
L(f)=1N∑n=1N(fw,b(xn)−y^n)2=1N∑n=1N(σ(zn)−y^n)2
损失函数对参数
wk
求偏导时:
∂L∂wk=1N∑n=1N∂(σ(zn)−y^n)2∂wk
=2N∑n=1N(σ(zn)−y^n)⋅∂σ(zn)∂zn⋅∂zn∂wk
其中,
∂σ(zn)∂zn=σ(zn)(1−σ(zn))
,
∂zn∂wk=xnk
。
代入得偏导结果:
∂L∂wk=2N∑n=1N(σ(zn)−y^n)⋅σ(zn)⋅(1−σ(zn))⋅xnk
=2N∑n=1N(fw,b(xn)−y^n)⋅fw,b(xn)⋅(1−fw,b(xn))⋅xnk

观察偏导结果,考察如下情况:
当第
n
个样本
xn
的真实类别是
C1
,有
y^n=1
。
若
fw,b(xn)=1
,说明预测的分类结果很接近真实类别,参数无需继续更新。而此时偏导结果
∂L∂wk=0
,确实是停止了参数的更新,很合理
但若
fw,b(xn)=0
,说明预测的分类结果与真实类别截然相反,参数距离目标还有很远,应该加大更新步伐。而此时偏导结果
∂L∂wk=0
,参数不再更新,显然不对

当第
n
个样本
xn
的真实类别是
C2
,有
y^n=0
。
若
fw,b(xn)=1
,说明预测的分类结果与真实类别截然相反,参数距离目标还有很远,应该加大更新步伐。而此时偏导结果
∂L∂wk=0
,参数不再更新,显然不对
若
fw,b(xn)=0
,说明预测的分类结果很接近真实类别,参数无需继续更新。此时偏导结果
∂L∂wk=0
,确实是停止了参数的更新,很合理

因此,当Logistic回归的损失函数取平方误差时,可能会出现参数更新无效率的问题。把参数与总损失(Total Loss)之间的变化作图可以更直观地反映问题,在损失函数分别取交叉熵和平均误差的情况下,假设中心位置是损失函数最低点:
- 黑色曲面为损失函数取交叉熵的情况,距离最低点越远,损失函数曲面越陡峭,偏导值越大,参数更新的步伐/速度也越快,这很合理。
- 红色曲面为损失函数取平均误差的情况,整个损失函数曲面比较平坦。在离最低点很远的地方,偏导值很小,参数更新的速度非常缓慢。而随机找一个参数初始值开始迭代,通常离最低点是很远的,如果参数更新很慢,就相当于卡在原地,很难到达最低点。虽然可以通过调整学习率使更新步伐变大,但偏导值很小的时候,我们并不能确定参数到底是在距离最低点很远的地方,还是已经到达最低点附近。如果已经到达最低点附近,学习率就不能调大,否则容易错过最低点。
所以,虽然损失函数取平方误差是可操作的,但不容易得到理想的参数结果,主要败在了参数更新效率上。

参考资料:
维基百科:交叉熵
交叉熵(Cross-Entropy)
交叉熵代价函数