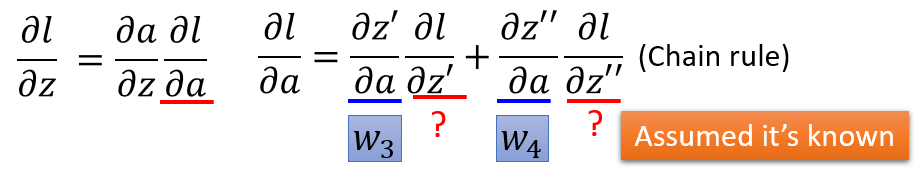ML Lecture 7: Backpropagation

ML Lecture 7: Backpropagation

• Youtube
• Bilibili
• 课件

---

反向传播算法

反向传播（Backpropagation，BP）是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的、用来训练人工神经网络的常见方法。该方法对网络中所有权重参数计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。

回顾梯度下降法求解最优参数：令损失函数$L(\theta)$对每一个参数分别求偏导，构成梯度向量$\nabla L(\theta)$，以学习率$\eta$不断迭代更新参数。当参数量十分庞大时，借助反向传播算法可以更高效地计算梯度。

---

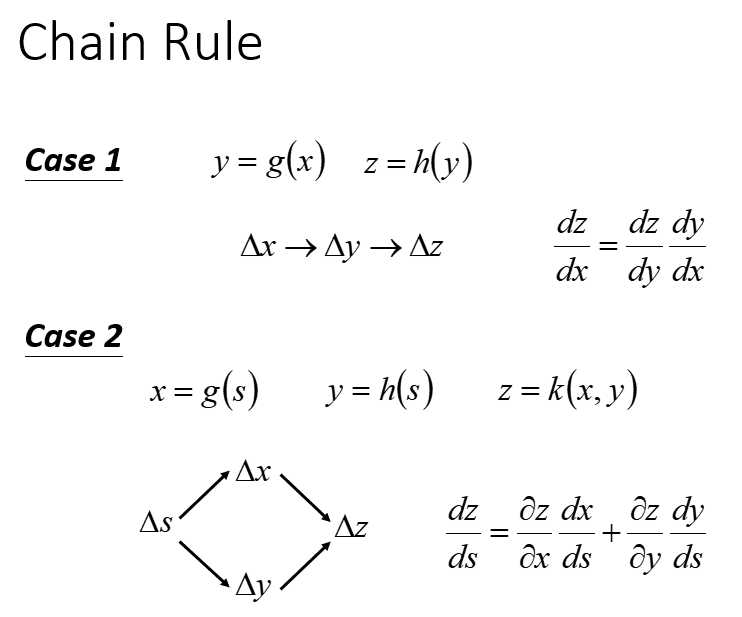
1. 链式法则（Chain Rule）回顾

• 对于两个函数$y = g(x)$和$z = h(y)$，自变量$x$的变化会引起$y$的变化，$y$的变化又会引起$z$的变化，这个连续的影响过程可以表示为：$\triangle x \to \triangle y \to \triangle z$。根据求导法则有：

  $$\frac{dz}{dx} = \frac{dz}{dy} \frac{dy}{dx}$$

• 对于函数$x = g(s)$、$y = h(s)$及二元函数$z = k(x, y)$，自变量$s$的变化会分别引起$x$、$y$的变化，而$x$、$y$的变化又会进一步影响$z$。根据链式求导法则，$s$是通过两条路径影响$z$的：

  $$\frac{dz}{ds} = \frac{\partial z}{\partial x} \frac{dx}{ds} + \frac{\partial z}{\partial y} \frac{dy}{ds}$$
  
  

---

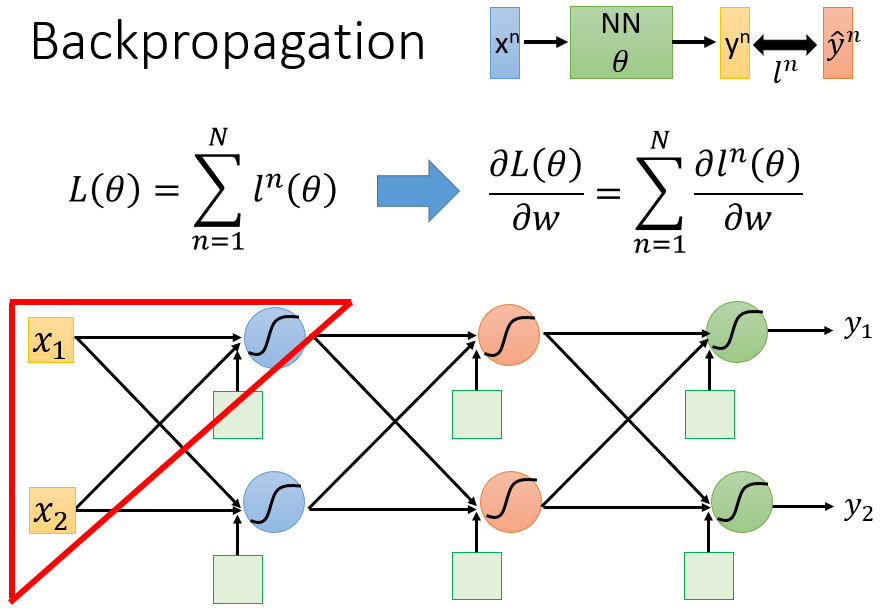
2. 反向传播（Backpropagation）的原理

首先明确，反向传播算法是一种辅助计算梯度向量的有效方法。利用反向传播算法计算出梯度后，就可以按照梯度下降法去更新参数。

在机器学习的第二个步骤中，我们定义了一个损失函数$L(\theta)$用于判断函数的优劣，这个损失函数$L(\theta)$是基于所有训练样本计算出来的。假设记第$n$个训练样本$x^n$的损失函数为$l^n(\theta)$，则$L(\theta) = \sum_{n=1}^N l^n(\theta)$。

在第三个步骤中，我们以损失函数$L(\theta)$最小化为目标寻找最优参数，需要计算$L(\theta)$对各个权重参数的偏导数。实际上，$L(\theta)$对某一个权重参数$w$的偏导数$\frac{\partial L(\theta)}{\partial w}$，即各个训练样本的损失函数$l(\theta)$分别对$w$求偏导，最后加总求和得到的：

$$\frac{\partial L(\theta)}{\partial w} = \sum_{n=1}^N \frac{\partial l^n (\theta)}{\partial w}$$

因此，损失函数的偏导数计算问题，就从计算$\frac{\partial L(\theta)}{\partial w}$转变为计算$\frac{\partial l(\theta)}{\partial w}$。

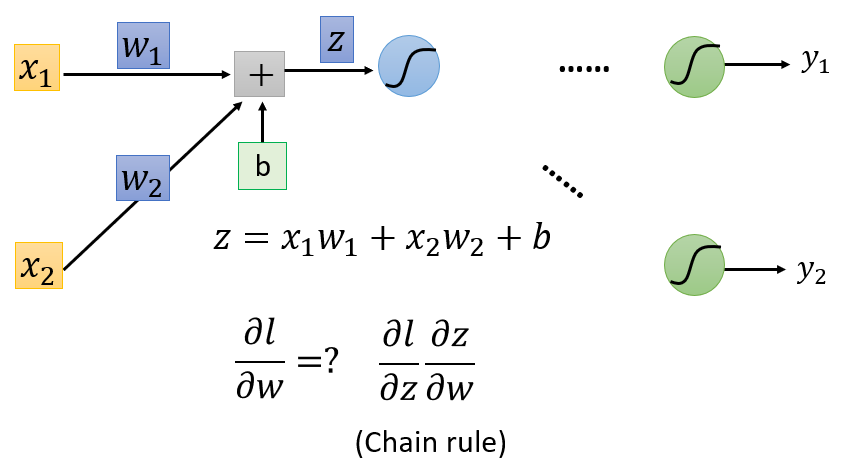
以其中一个神经元为例：假设该神经元的参数为$\theta = (w_1, w_2, b)$，输入样本$x$是一个二维向量$\left[ \begin{matrix} x_1 \\ x_2 \\ \end{matrix} \right]$，则样本$x$在这个神经元里，经过了一个线性变换（并在后续神经元里经过一系列转换，得到最后的输出$y$）：

$$z = w_1 x_1 + w_2 x_2 + b$$

记样本$x$的损失函数$l$，对于参数$\theta$中的权重参数$w_1$（或$w_2$）的偏导数为$\frac{\partial l}{\partial w_1}$（或$\frac{\partial l}{\partial w_2}$），则根据链式求导法则有：

$$\frac{\partial l}{\partial w} = \frac{\partial l}{\partial z} \frac{\partial z}{\partial w}$$
其中， $w=w_1$或 $w_2$。这里的影响路径是：改变参数 $w$，就会影响线性变换的结果 $z$，而 $z$会进一步影响损失函数 $l$。

因此，损失函数的偏导数计算问题，就从计算$\frac{\partial l(\theta)}{\partial w}$转变为计算$\frac{\partial l}{\partial z}$和$\frac{\partial z}{\partial w}$。 其中，第一项$\frac{\partial l}{\partial z}$称为反向传播（Backward Pass）；第二项$\frac{\partial z}{\partial w}$称为前向传播（Forward Pass）。

（1）前向传播阶段（Forward Pass）计算$\frac{\partial z}{\partial w}$

前向传播阶段的计算十分简单。需要计算的偏导数为$\frac{\partial z}{\partial w}$，以上面单个神经元为例，线性变换$z = w_1 x_1 + w_2 x_2 + b$，则$2$个权重参数的偏导数分别为：

$$\frac{\partial z}{\partial w_1} = x_1$$ $$\frac{\partial z}{\partial w_2} = x_2$$ 偏导数的计算结果恰好是这个神经元的输入 $x = \left[ \begin{matrix} x_1 \\ x_2 \\ \end{matrix} \right]$

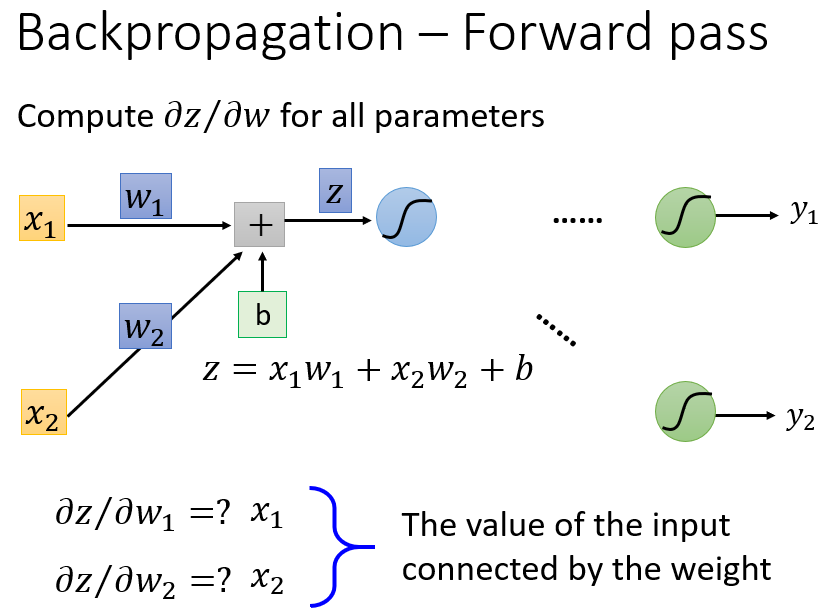
上面是单个神经元对自身各权重参数求偏导的情况。以此类推，任何一个神经元对自身权重参数的偏导，就是该神经元的输入值。

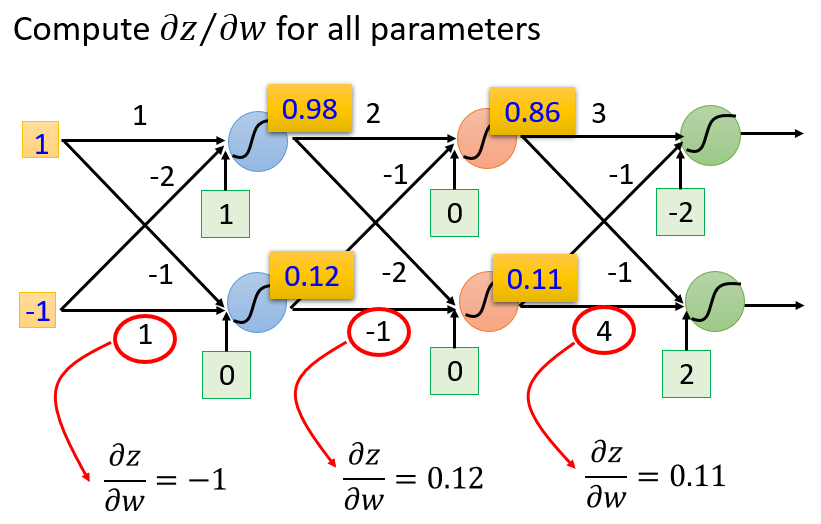
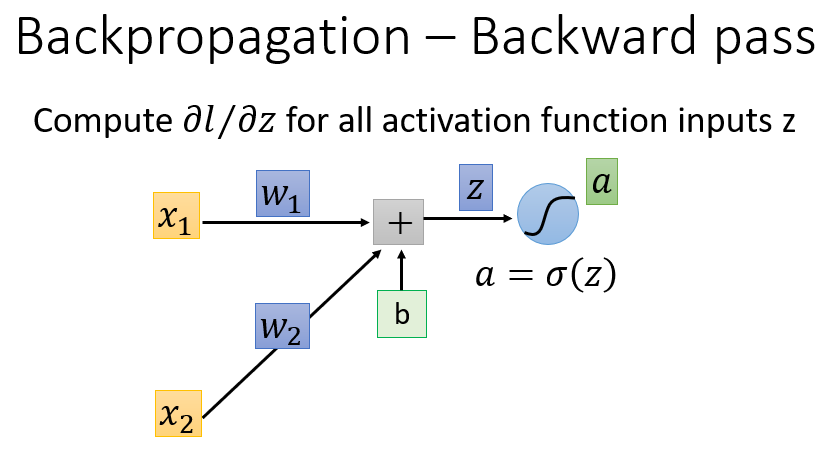
（2）反向传播阶段（Backward Pass）计算$\frac{\partial l}{\partial z}$

反向传播阶段计算的偏导数为$\frac{\partial l}{\partial z}$。首先考察线性变换$z$是如何影响损失函数$l$的：$z$通过一个激活函数$\sigma()$后，得到$a$。因此，$z$是通过影响$a$的值，进而影响损失函数$l$的值。
【注】：这里的激活函数是Sigmoid函数$\sigma(z)$，现在比较常用的是ReLU、tanh等激活函数，详见神经网络之激活函数(Activation Function)。

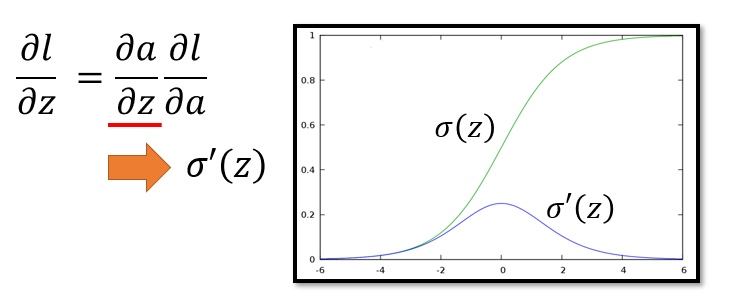
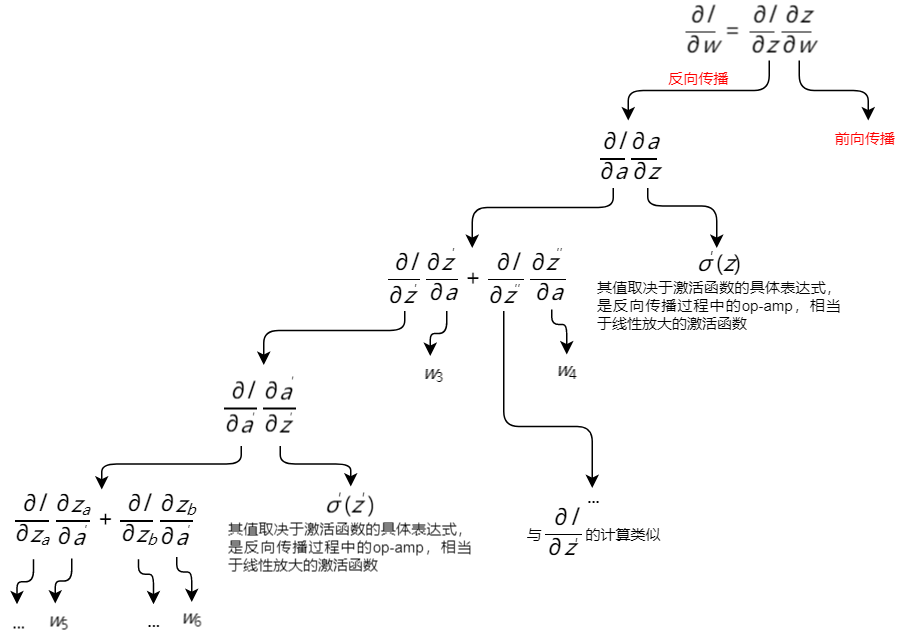
根据链式法则，偏导数$\frac{\partial l}{\partial z} = \frac{\partial l}{\partial a} \frac{\partial a}{\partial z}$。
其中$\frac{\partial a}{\partial z}$这一项取决于激活函数的具体表达式，计算比较简单。以Sigmoid函数$a = \sigma(z) = \frac{1}{1 + e^{-z}}$为例，偏导数$\frac{\partial a}{\partial z} = \sigma^{'} (z) = \sigma(z) (1 - \sigma(z))$。若在同一坐标图上画出$\sigma(z)$和$\sigma^{'}(z)$的形状：由于$\sigma(z)$左右两端变化慢，中间段斜率很大，所以$\sigma^{'}(z)$的两端趋近于$0$，在中间位置达到最大值，如下图。

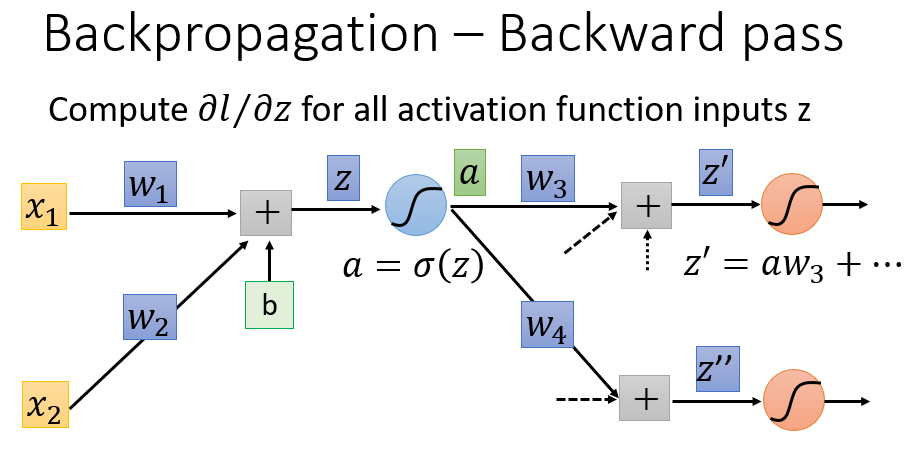
而另外一项$\frac{\partial l}{\partial a}$的计算则比较复杂，涉及到所谓的“反向传播”。经过第一层Sigmoid函数转化后，得到的$a = \sigma(z)$，将传入下一层的每一个神经元，所以$a$会影响到后面所有神经元。现在假设$a$后面还有两个神经元，显然$a$会影响到$z^{'}$和$z^{''}$：$z^{'} = a w_3$、$z^{''} = a w_4$。

因此，$\frac{\partial l}{\partial a}$就要继续按照链式法则展开，写成：$\frac{\partial l}{\partial a} = \frac{\partial l}{\partial z^{'}} \frac{\partial z^{'}}{\partial a} + \frac{\partial l}{\partial z^{''}} \frac{\partial z^{''}}{\partial a}$。
其中，$\frac{\partial z^{'}}{\partial a} = w_3$，$\frac{\partial z^{''}}{\partial a} = w_4$。

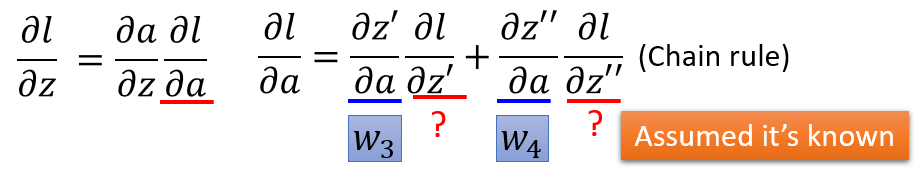
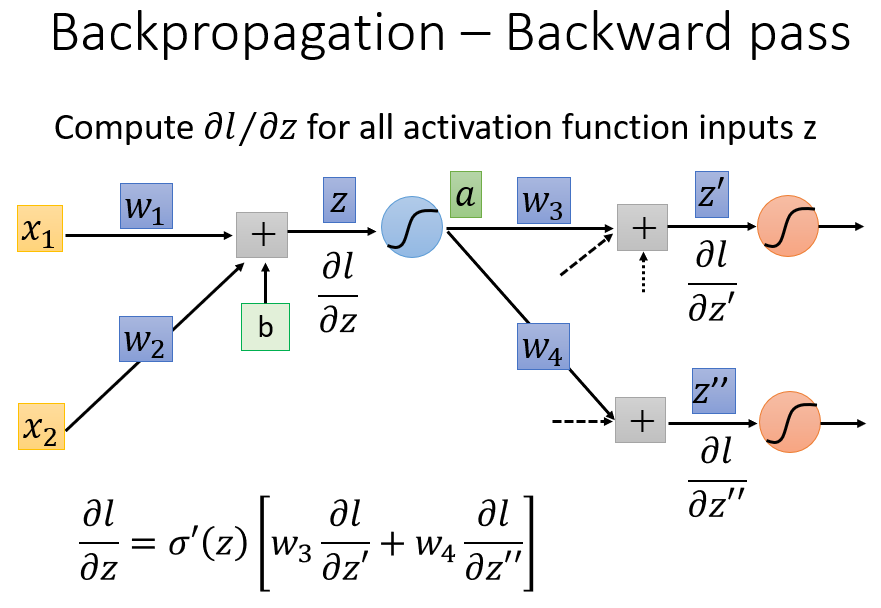
则反向传播阶段所要计算的偏导数$\frac{\partial l}{\partial z}$就可以总结为：

$$\frac{\partial l}{\partial z} = \frac{\partial l}{\partial a} \frac{\partial a}{\partial z} = (w_3 \frac{\partial l}{\partial z^{'}} + w_4 \frac{\partial l}{\partial z^{''}}) \sigma^{'}(z)$$

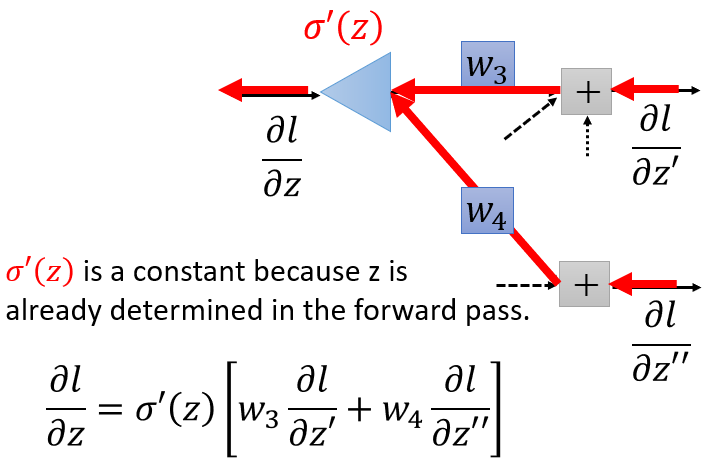
上面的式子可以从反向传播的角度来解读：把这个式子视为一个线性的神经元，一般我们认为神经元就是把输入值$x$在权重参数$w$的作用下，加上偏置值，通过激活函数，得到输出值。上述式子可以把$\frac{\partial l}{\partial z^{'}}$、$\frac{\partial l}{\partial z^{''}}$视为输入，把$w_3$、$w_4$视为权重，经过一个线性的激活函数，相当于经过一个运算放大器（Operational Amplifier，op-amp），即乘上一个常数$\sigma^{'}(z)$，得到输出$\frac{\partial l}{\partial z}$。

至此，剩下的问题就是如何求得$\frac{\partial l}{\partial z^{'}}$和$\frac{\partial l}{\partial z^{''}}$，分为如下两种情况讨论：

1. 若$z^{'}$和$z^{''}$通过激活函数后，得到的就是输出值，即已经抵达终点。那么由链式法则：

   $$\frac{\partial l}{\partial z^{'}} = \frac{\partial l}{\partial y_1} \frac{\partial y_1}{\partial z^{'}}$$ $$\frac{\partial l}{\partial z^{''}} = \frac{\partial l}{\partial y_2} \frac{\partial y_2}{\partial z^{''}}$$
   
   

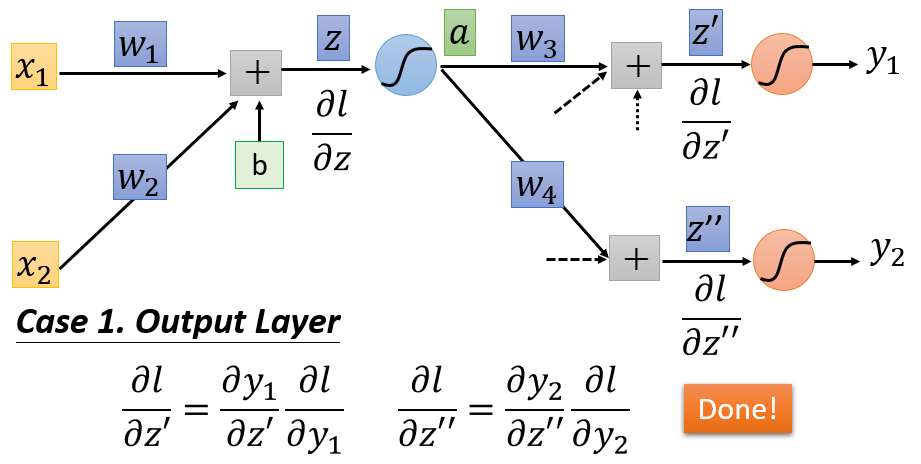
2. 若$z^{'}$和$z^{''}$通过激活函数后，还未到达输出层，后面还连接有其他神经元，那么链式法则就继续延伸。以$z^{'}$为例，其通过激活函数后，得到$a^{'}$，现在假设后面还有两个神经元$z_a$和$z_b$。显然$a^{'}$会影响到$z_a$和$z_b$：$z_a = a^{'} w_5$、$z_b = a^{'} w_6$。
   

   

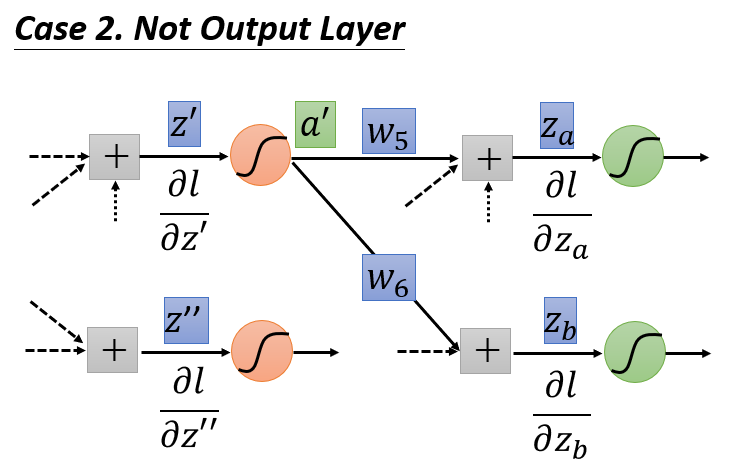
   那么根据链式法则：$\frac{\partial l}{\partial z^{'}} = \frac{\partial l}{\partial a^{'}} \frac{\partial a^{'}}{\partial z^{'}} = [\frac{\partial l}{\partial z_a} \frac{\partial z_a}{\partial a^{'}} + \frac{\partial l}{\partial z_b} \frac{\partial z_b}{\partial a^{'}}] \frac{\partial a^{'}}{\partial z^{'}} = [\frac{\partial l}{\partial z_a} w_5 + \frac{\partial l}{\partial z_b} w_6] \sigma^{'}(z^{'})$。

   同理，可以计算$\frac{\partial l}{\partial z^{''}}$。

   偏导数$\frac{\partial l}{\partial z}$的整个运算过程归纳如下。如果从Input的方向从前往后看，随着神经元个数不断增加，运算量以递归的形式不断增大。
   

   

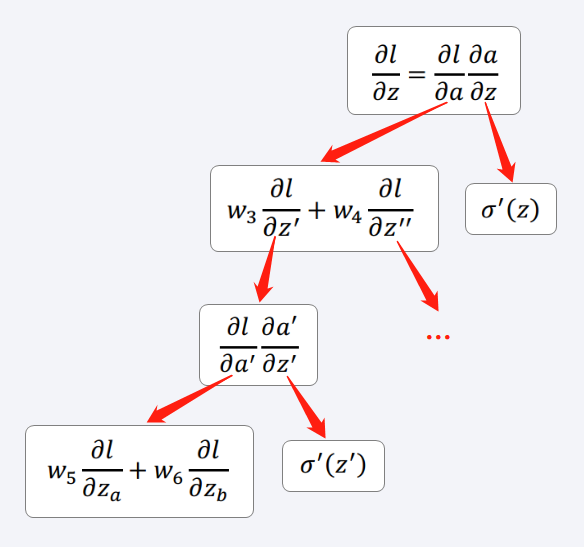
   容易观察：只要知道$\frac{\partial l}{\partial z_a}$和$\frac{\partial l}{\partial z_b}$，就能够计算出$\frac{\partial l}{\partial a^{'}}$，进而求出$\frac{\partial l}{\partial z^{'}}$；只要知道$\frac{\partial l}{\partial z^{'}}$和$\frac{\partial l}{\partial z^{''}}$，就能够计算出$\frac{\partial l}{\partial a}$，进而求出$\frac{\partial l}{\partial z}$。这里，$\sigma^{'}(z)$和$\sigma^{'}(z^{'})$相当于两个线性放大器op-amp。如果神经元个数继续增加，那么$\frac{\partial l}{\partial z_a}$和$\frac{\partial l}{\partial z_b}$就要继续往后做递归推算，直到抵达输出层。

   而从Output的方向出发，从后往前看，计算量会大大减少。
   

   

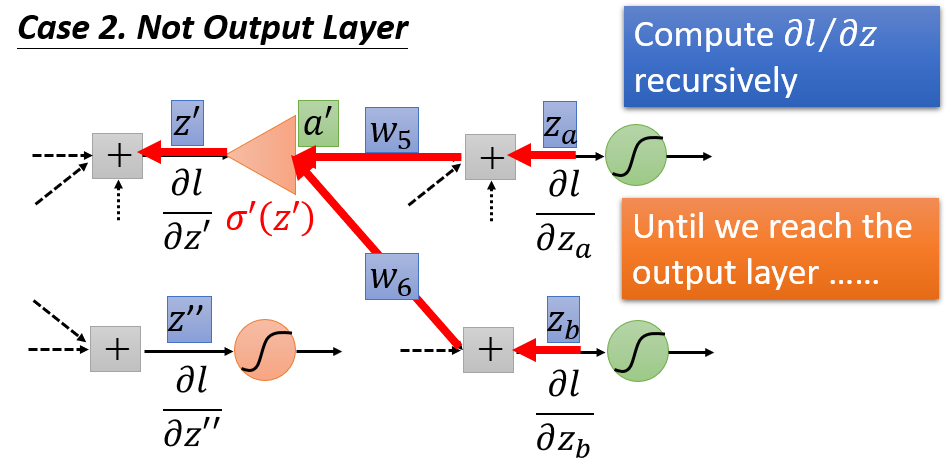
   假设一共有如下$6$个神经元：
   

   

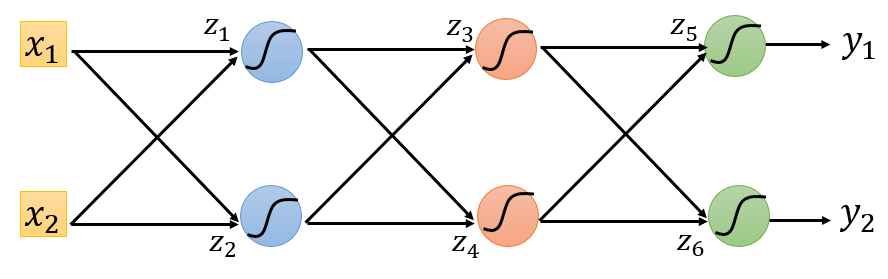
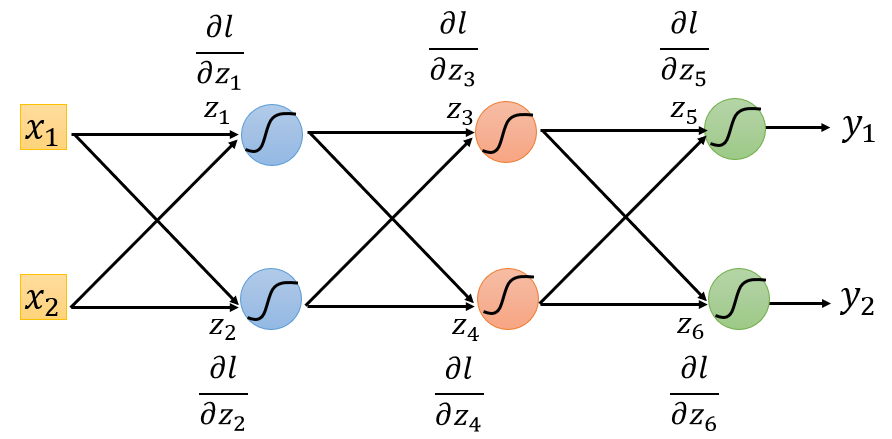
   • 如果从前往后看，要求出$\frac{\partial l}{\partial z_1}$，就必须先知道$\frac{\partial l}{\partial z_3}$和$\frac{\partial l}{\partial z_4}$；要求出$\frac{\partial l}{\partial z_3}$，就必须先知道$\frac{\partial l}{\partial z_5}$和$\frac{\partial l}{\partial z_6}$，运算过程很复杂
     

     

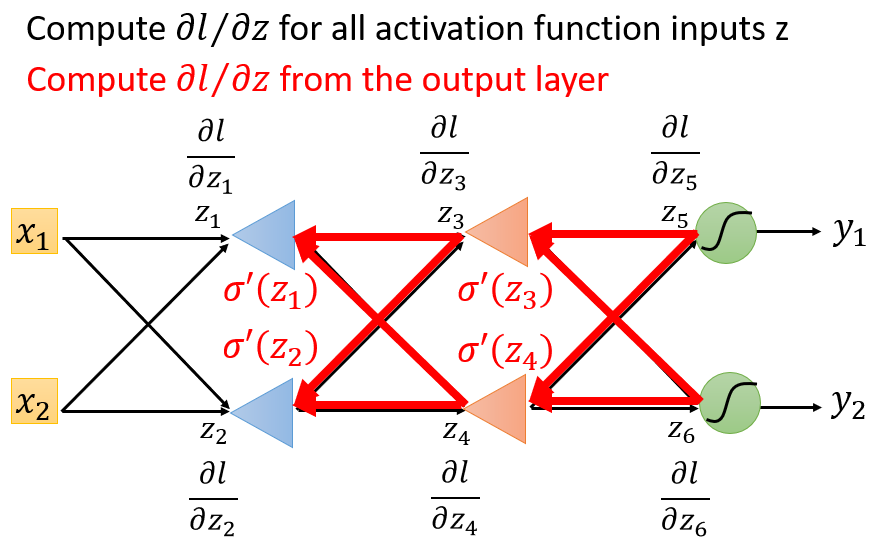
   • 如果从后往前看，这个问题就被简化了。如下图，把原来的神经网络通通逆转，把所有神经元全部用op-amp取代，放大倍率就是原神经元的激活函数的导数：$\sigma^{'}(z_1)...\sigma^{'}(z_4)$。
     先计算$\frac{\partial l}{\partial z_5}$和$\frac{\partial l}{\partial z_6}$，这两个偏导的计算是简单的，因为它们连接着输出层。分别经过op-amp$\sigma^{'}(z_3)$和$\sigma^{'}(z_4)$后，求出$\frac{\partial l}{\partial z_3}$和$\frac{\partial l}{\partial z_4}$。
     再将$\frac{\partial l}{\partial z_3}$和$\frac{\partial l}{\partial z_4}$经过op-amp$\sigma^{'}(z_1)$和$\sigma^{'}(z_2)$，求出$\frac{\partial l}{\partial z_1}$和$\frac{\partial l}{\partial z_2}$。
     注意到，这个运算过程与完全连接前馈式神经网络的计算量是一样的。
     

     

---

总结

将神经网络简化为如下构造：

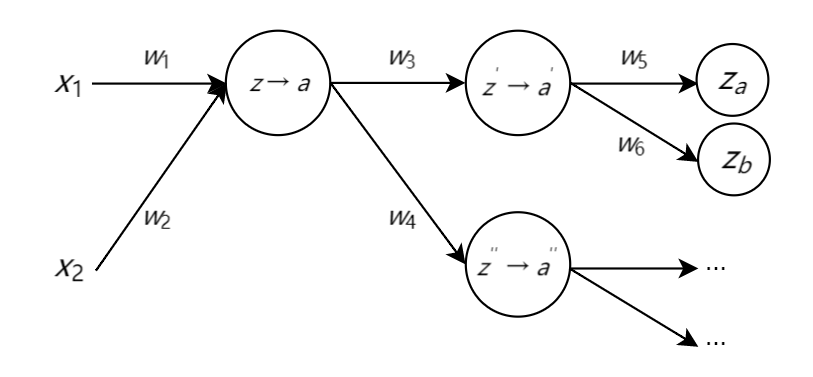
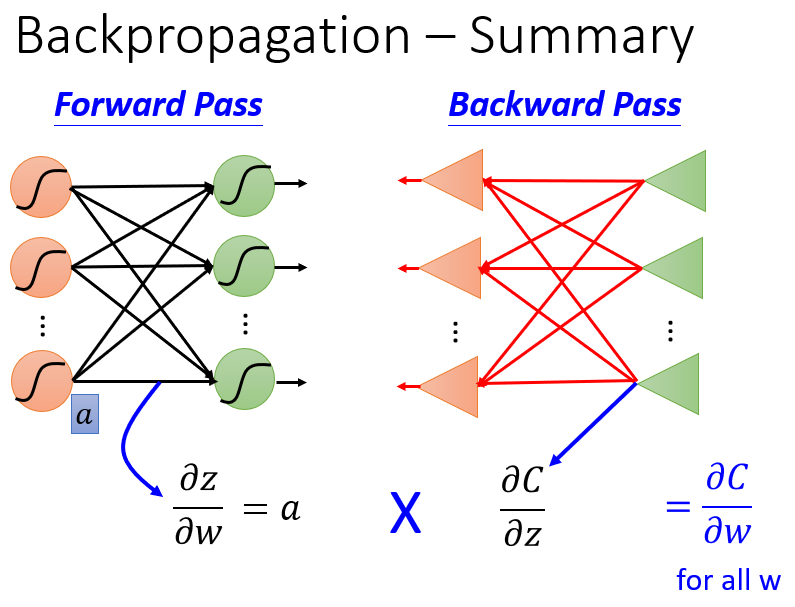
则在反向传播算法中，各个计算过程分别为：

1. 前向传播阶段（Forward Pass）的目标是计算$\frac{\partial z}{\partial w}$
   我们需要知道最开始的输入值，以及每一层各个神经元的输出，这些值就是各个神经元所对应的权重参数的偏导数$\frac{\partial z}{\partial w}$
2. 反向传播阶段（Backward Pass）的目标是计算$\frac{\partial l}{\partial z}$
   先把神经网络逆转，用op-amp替换所有神经元，从后往前计算各个神经元的$\frac{\partial l}{\partial z}$

最后，将$\frac{\partial z}{\partial w}$和$\frac{\partial l}{\partial z}$相乘，就可以得到单个样本的损失函数$l$对神经元中各权重参数$w$的偏导数$\frac{\partial l}{\partial w}$，用反向传播算法可以简单地将整个神经网络里的所有权重参数的偏导值求出来，构成一个梯度向量，这个梯度向量可以根据梯度下降法对参数进行更新。

参考资料：
维基百科：反向传播算法
一小时神经网络从入门到精通(放弃)
如何直观地解释 back propagation 算法？
手撸反向传播算法+代码实现

---

计算实栗

根据反向传播算法的过程：

其中，$\nabla_a$是求梯度运算符，$\nabla_a C = \frac{\partial C}{\partial a^L}$是一个向量，$L$表示最后一层（输出层）。

假设有如下三层神经网络：

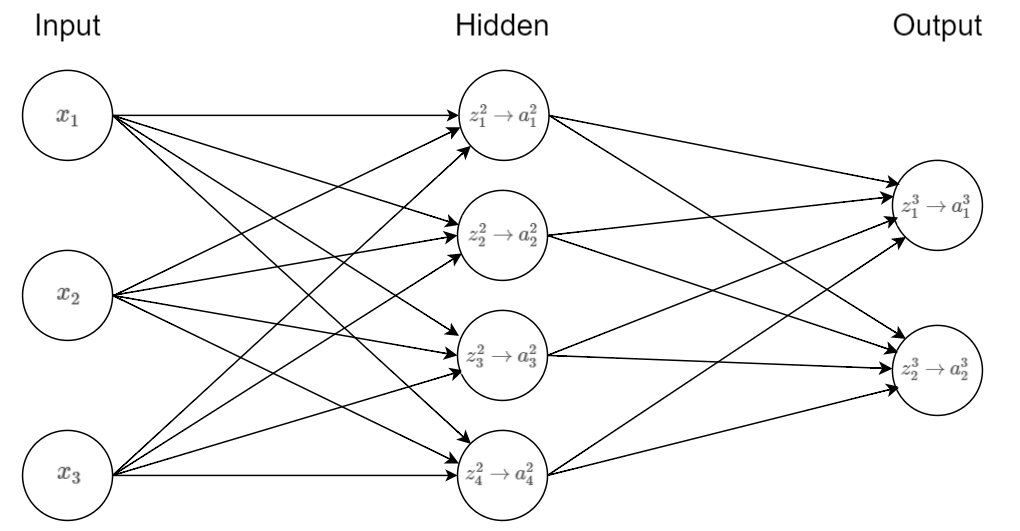
• 第一个输入层：样本$x = \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix} \right]$

• 第二个隐藏层有$4$个神经元：权重矩阵为$W^2 = \left[ \begin{matrix} w^2_{11} & w^2_{12} & w^2_{13} \\ w^2_{21} & w^2_{22} & w^2_{23} \\ w^2_{31} & w^2_{32} & w^2_{33} \\ w^2_{41} & w^2_{42} & w^2_{43} \end{matrix} \right]_{4 \times 3}$，偏置矩阵为$b^2 = \left[ \begin{matrix} b^2_1 \\ b^2_2 \\ b^2_3 \\ b^2_4 \end{matrix} \right]$
  带权输入为$z^2 = \left[ \begin{matrix} z^2_1 \\ z^2_2 \\ z^2_3 \\ z^2_4 \end{matrix} \right]$，激活向量为$a^2 = \left[ \begin{matrix} a^2_1 \\ a^2_2 \\ a^2_3 \\ a^2_4 \end{matrix} \right]$

• 第三个输出层有$2$个神经元：权重矩阵为$W^3 = \left[ \begin{matrix} w^3_{11} & w^3_{12} & w^3_{13} & w^3_{14} \\ w^3_{21} & w^3_{22} & w^3_{23} & w^3_{24} \end{matrix} \right]_{2 \times 4}$，偏置矩阵为$b^3 = \left[ \begin{matrix} b^3_1 \\ b^3_2 \end{matrix} \right]$
  带权输入为$z^3 = \left[ \begin{matrix} z^3_1 \\ z^3_2 \end{matrix} \right]$，激活向量为$a^3 = \left[ \begin{matrix} a^3_1 \\ a^3_2 \end{matrix} \right]$

【注】：第$l$个隐藏层的参数矩阵$W^l$，它的行数是该隐藏层（第$l$层）的神经元个数，它的列数是上一层（第$l-1$层）传过来的列向量的维数。

实际计算过程如下：

1. 输入：样本$x$，作为输入层的激活值$a^1 = x = \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix} \right]$

2. 前向传播：当$l = 2,3$，计算$z_2,a_2,z_3,a_3$：

   $z^2 = W^2 a^1 + b^2 = \left[ \begin{matrix} w^2_{11} & w^2_{12} & w^2_{13} \\ w^2_{21} & w^2_{22} & w^2_{23} \\ w^2_{31} & w^2_{32} & w^2_{33} \\ w^2_{41} & w^2_{42} & w^2_{43} \end{matrix} \right] \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix} \right] + \left[ \begin{matrix} b^2_1 \\ b^2_2 \\ b^2_3 \\ b^2_4 \end{matrix} \right] = \left[ \begin{matrix} w^2_{11} x_1 + w^2_{12} x_2 + w^2_{13} x_3 + b^2_1\\ w^2_{21} x_1 + w^2_{22} x_2 + w^2_{23} x_3 + b^2_2 \\ w^2_{31} x_1 + w^2_{32} x_2 + w^2_{33} x_3 + b^2_3 \\ w^2_{41} x_1 + w^2_{42} x_2 + w^2_{43} x_3 + b^2_4 \end{matrix} \right] = \left[ \begin{matrix} z^2_1 \\ z^2_2 \\ z^2_3 \\ z^2_4 \end{matrix} \right]$

   $a^2 = \sigma(z^2) = \left[ \begin{matrix} \sigma(w^2_{11} x_1 + w^2_{12} x_2 + w^2_{13} x_3 + b^2_1) \\ \sigma(w^2_{21} x_1 + w^2_{22} x_2 + w^2_{23} x_3 + b^2_2) \\ \sigma(w^2_{31} x_1 + w^2_{32} x_2 + w^2_{33} x_3 + b^2_3) \\ \sigma(w^2_{41} x_1 + w^2_{42} x_2 + w^2_{43} x_3 + b^2_4) \end{matrix} \right] = \left[ \begin{matrix} a^2_1 \\ a^2_2 \\ a^2_3 \\ a^2_4 \end{matrix} \right]$

   $z^3 = W^3 a^2 + b^3 = \left[ \begin{matrix} w^3_{11} & w^3_{12} & w^3_{13} & w^3_{14} \\ w^3_{21} & w^3_{22} & w^3_{23} & w^3_{24} \end{matrix} \right] \left[ \begin{matrix} a^2_1 \\ a^2_2 \\ a^2_3 \\ a^2_4 \end{matrix} \right] + \left[ \begin{matrix} b^3_1 \\ b^3_2 \end{matrix} \right]= \left[ \begin{matrix} w^3_{11} a^2_1 + w^3_{12} a^2_2 + w^3_{13} a^2_3 + w^3_{14} a^2_4 + b^3_1 \\ w^3_{21} a^2_1 + w^3_{22} a^2_2 + w^3_{23} a^2_3 + w^3_{24} a^2_4 + b^3_2 \end{matrix} \right] = \left[ \begin{matrix} z^3_1 \\ z^3_2 \end{matrix} \right]$

   $a^3 = \sigma(z^3) = \left[ \begin{matrix} \sigma(w^3_{11} a^2_1 + w^3_{12} a^2_2 + w^3_{13} a^2_3 + w^3_{14} a^2_4 + b^3_1) \\ \sigma(w^3_{21} a^2_1 + w^3_{22} a^2_2 + w^3_{23} a^2_3 + w^3_{24} a^2_4 + b^3_2) \end{matrix} \right] = \left[ \begin{matrix} a^3_1 \\ a^3_2 \end{matrix} \right]$

3. 计算输出层误差向量$\delta^3$：

   $\delta^3 = \nabla_a C \odot \sigma^{'}(z^3) = \frac{\partial C}{\partial a^3} \odot \sigma^{'}(z^3) = \left[ \begin{matrix} \frac{\partial C}{\partial a^3_1} \\ \frac{\partial C}{\partial a^3_2} \end{matrix} \right] \odot \left[ \begin{matrix} \sigma^{'}(z^3_1) \\ \sigma^{'}(z^3_2) \end{matrix} \right] = \left[ \begin{matrix} \frac{\partial C}{\partial a^3_1} \cdot \sigma^{'}(z^3_1) \\ \frac{\partial C}{\partial a^3_2} \cdot \sigma^{'}(z^3_2) \end{matrix} \right] = \left[ \begin{matrix} \delta^3_1 \\ \delta^3_2 \end{matrix} \right]$

4. 计算反向误差传播$\delta^2$：

   $\delta^2 = ((W^3)^T \delta^3) \odot \sigma^{'}(z^2) = (\left[ \begin{matrix} w^3_{11} & w^3_{12} & w^3_{13} & w^3_{14} \\ w^3_{21} & w^3_{22} & w^3_{23} & w^3_{24} \end{matrix} \right]^T \left[ \begin{matrix} \delta^3_1 \\ \delta^3_2 \end{matrix} \right]) \odot \left[ \begin{matrix} \sigma^{'}(z^2_1) \\ \sigma^{'}(z^2_2) \\ \sigma^{'}(z^2_3) \\ \sigma^{'}(z^2_4) \end{matrix} \right] = \left[ \begin{matrix} (w^3_{11} \delta^3_1 + w^3_{21} \delta^3_2) \cdot \sigma^{'}(z^2_1) \\ (w^3_{12} \delta^3_1 + w^3_{22} \delta^3_2) \cdot \sigma^{'}(z^2_2) \\ (w^3_{13} \delta^3_1 + w^3_{23} \delta^3_2) \cdot \sigma^{'}(z^2_3) \\ (w^3_{14} \delta^3_1 + w^3_{24} \delta^3_2) \cdot \sigma^{'}(z^2_4) \end{matrix} \right] = \left[ \begin{matrix} \delta^2_1 \\ \delta^2_2 \\ \delta^2_3 \\ \delta^2_4 \end{matrix} \right]$

5. 代价函数的梯度元素计算公式为：$\frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \cdot \delta^l_j$和$\frac{\partial C}{\partial b^l_j} = \delta^l_j$，以计算偏导数$\frac{\partial C}{\partial w^2_{11}}$为例：

   由公式：

   $$\frac{\partial C}{\partial w^2_{11}} = a^1_1 \cdot \delta^2_1 = x_1 \cdot \delta^2_1$$

   由链式法则：

   $$\frac{\partial C}{\partial w^2_{11}} = \frac{\partial z^2_1}{\partial w^2_{11}} \frac{\partial a^2_1}{\partial z^2_1} \frac{\partial z^3_1}{\partial a^2_1} \frac{\partial a^3_1}{\partial z^3_1} \frac{\partial C}{\partial a^3_1} + \frac{\partial z^2_1}{\partial w^2_{11}} \frac{\partial a^2_1}{\partial z^2_1} \frac{\partial z^3_2}{\partial a^2_1} \frac{\partial a^3_2}{\partial z^3_2} \frac{\partial C}{\partial a^3_2}$$
   $$= x_1 \cdot \sigma^{'}(z^2_1) \cdot w^3_{11} \cdot \sigma^{'}(z^3_1) \cdot \frac{\partial C}{\partial a^3_1} + x_1 \cdot \sigma^{'}(z^2_1) \cdot w^3_{21} \cdot \sigma^{'}(z^3_2) \cdot \frac{\partial C}{\partial a^3_2}$$
   $$= x_1 \cdot \sigma^{'}(z^2_1) \cdot [w^3_{11} \cdot \sigma^{'}(z^3_1) \cdot \frac{\partial C}{\partial a^3_1} + w^3_{21} \cdot \sigma^{'}(z^3_2) \cdot \frac{\partial C}{\partial a^3_2}]$$
   $$= x_1 \cdot \sigma^{'}(z^2_1) \cdot [w^3_{11} \cdot \delta^3_1 + w^3_{21} \cdot \delta^3_2]$$
   $$= x_1 \cdot \delta^2_1$$

因此，由反向传播计算公式与链式法则的计算结果完全一致。