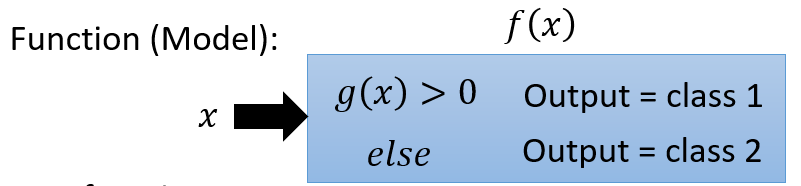ML Lecture 4: Classification——Probabilistic Generative Model（上）

ML Lecture 4: Classification——Probabilistic Generative Model

分类问题：概率生成模型

在分类问题中，输入是样本 $x$ 的一系列特征，输出是样本 $x$ 属于哪一类。

例如：

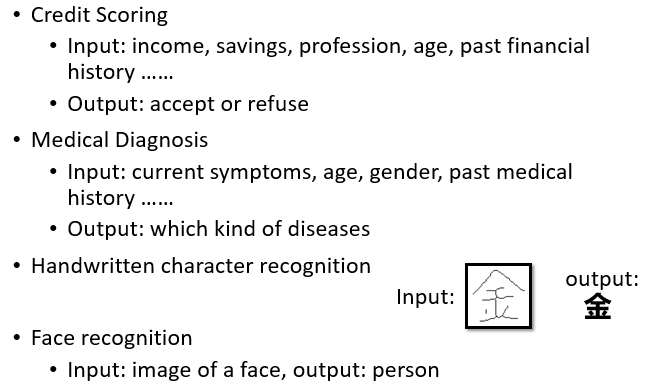
金融上用分类模型，决定是否贷款给某个客户：寻找一个模型，输入值是一个客户的收入、存款、工作、年龄、过去的消费记录等，输出是/否贷款
做医疗诊断，判断得病类型：输入值是症状、年龄、性别、过去的得病记录等，输出得哪一种病
手写文字辨识：输入手写文字的图像，输出文字属于哪一个汉字。在中文手写辨识问题里，大约有 $8000$ 个字符，所以这个分类问题中包含着 $8000$ 多个类别，模型的输出就是从这 $8000$ 多个类别里面选一个
人脸辨识：输入人脸图像，输出身份

能否用回归方法解决分类问题？

首先，分类问题的训练集是成对数据（pair）： $(x^1, \hat y^1)$ 、 $(x^2, \hat y^2)$ … $(x^N, \hat y^N)$ 。其中，第 $n$ 个样本 $x^n$ 是一个向量，其中包含能够描述该样本情况的一系列值（例如，pokemon的生命值、攻击力、防御力、速度等）； $\hat y^n$ 是该样本对应的真实类别。

以二分类问题（Binary Classification）为例，其输出结果只有两种。假如把二分类问题看作回归问题来解决，那么：

在训练集中，当样本属于第一类时，输出结果记为 $\hat y = 1$ ；当样本属于第二类时，输出结果记为 $\hat y = -1$ ，强行训练出回归模型
在测试集上，根据回归模型预测出来的 $y$ 值（这个值不会正好是 $1$ 或 $-1$ ，而是任意一个可能的数值），把 $y$ 值接近 $1$ 的样本归入第一类，把 $y$ 值接近 $-1$ 的样本归入第二类

问题就转变为：以 $y = 0$ 为分界，若回归模型的输出值 $y > 0$ ，就归为第一类；若回归模型的输出值 $y < 0$ ，就归为第二类。但是，这种做法是有缺陷的。

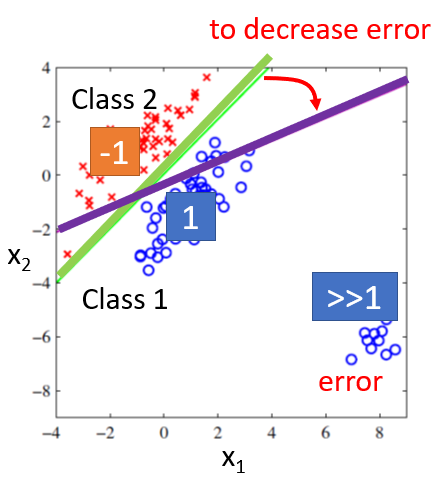
以下图训练集数据为例，假设 $x_1$ 、 $x_2$ 分别代表样本的两个不同特征，蓝色代表样本属于第一类，红色代表样本属于第二类，利用训练集建立回归模型 $y = b + w_1 x_1 + w_2 x_2$ 。

我们希望模型能够满足：蓝色样本的特征值输入回归模型，得到的 $y$ 值尽量接近 $1$ ；红色样本的特征值输入该模型，得到的 $y$ 值尽量接近 $-1$ 。

在数据分布比较理想的情况下（没有异常值），找到符合条件的参数 $w = \left[ \begin{matrix} w_1\\ w_2 \\ \end{matrix} \right]$ 、 $b$ 并不难。此时绿色直线 $b + w_1 x_1 + w_2 x_2 = 0$ 就成为两个类别的分界线，线上任意一点 $(x_1,x_2)$ 对应的输出值 $y$ 为 $0$ 。直线左上区域代表模型输出值小于 $0$ ，样本归为第二类；直线右下区域代表模型输出值大于 $0$ ，样本归为第一类
而在数据分布不理想的情况下，例如第一类样本（蓝色点），虽然同为一类，但分布并不均匀。直观来看，划分第一、二类的良好分界线应该仍然是绿色线。
但是对回归方法而言，为了更好地拟合右下角的离群点，回归方法会调整参数，给出新的分界——紫色线，而紫色线的分类效果显然不如绿色线。

在上述例子中，回归模型认为紫色线是最佳函数，而实际上用于分类的最佳函数是绿色线。所以，用回归模型去解决分类问题存在如下问题：

回归模型中定义损失函数的方式（平方损失函数），并不适用于分类问题
回归模型在训练过程中，会惩罚一些输出值过大的样本（太过于正确），最后训练出来的回归模型分类效果反而不好
此外，在分类问题中，不同类别之间应该具有同等地位。如果强行用回归方法去解决，就必须为每个真实类别定义不同的输出值：例如第一类的真实输出记为 $\hat y = 1$ ，第二类的真实输出记为 $\hat y = 2$ ，第三类的真实输出记为 $\hat y = 3$ ，…，这样就隐含着“类别 $1$ 与类别 $2$ 更接近”，“类别 $2$ 与类别 $3$ 更接近”的假设，显然不合适

如何解决分类问题？

解决分类问题的方法有多种，一个可能的想法是：以二元分类为例，在我们要寻找的函数 $f$ 里，内建另外一个函数 $g$ 。如果 $g(x) > 0$ ，就判为第一类，否则判为第二类
损失函数定义为：选定某个函数 $f$ ，在训练集上做分类预测，它预测错误的次数。如果 $f$ 在训练集上预测分类的错误次数越少，代表损失函数越小，函数 $f$ 就越好。 $f(x^n)$ 是函数 $f$ 对第 $n$ 个样本 $x^n$ 的分类结果， $\hat y^n$ 是 $x^n$ 的真实类别， $\delta()$ 函数代表：若括号内的条件成立，则输出 $1$ ，否则输出 $0$
找到最优函数，可以通过感知机（Perceptron）、SVM等

以下暂不探讨感知机、SVM，而是从概率的角度出发，介绍概率生成模型，该方法与机器学习的三个步骤其实是一样的。

问题引入

1. 盒子取球问题

给定两个盒子，其内都装有蓝、绿两种颜色的球，不同颜色的球个数如下图。已知现在取得一个蓝色球，问这个球来自两个盒子的概率分别有多大？

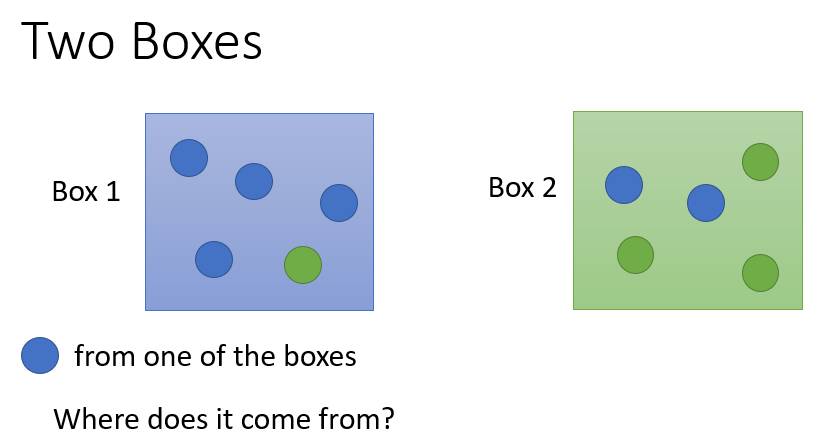
假设先验分布：选择盒 $1$ 的概率为 $P(B_1) = \frac{2}{3}$ ，选择盒 $2$ 的概率为 $P(B_2) = \frac{1}{3}$

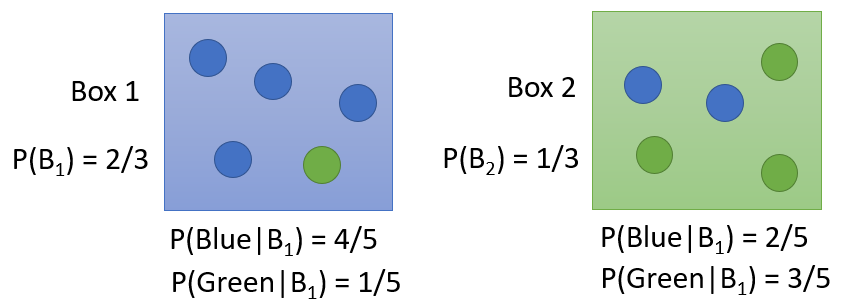
则根据条件概率公式可以分别求出蓝球来自盒 $1$ 、盒 $2$ 的概率：

蓝色球来自盒 $1$ 的概率： $P (B_{1} | B l u e) = \frac{P (B l u e | B_{1}) P (B_{1})}{P (B l u e | B_{1}) P (B_{1}) + P (B l u e | B_{2}) P (B_{2})}$ $P(B_1|Blue) = \frac{P(Blue|B_1) P(B_1)}{P(Blue|B_1) P(B_1) + P(Blue|B_2) P(B_2)}$
蓝色球来自盒 $2$ 的概率： $P (B_{2} | B l u e) = \frac{P (B l u e | B_{2}) P (B_{2})}{P (B l u e | B_{1}) P (B_{1}) + P (B l u e | B_{2}) P (B_{2})}$ $P(B_2|Blue) = \frac{P(Blue|B_2) P(B_2)}{P(Blue|B_1) P(B_1) + P(Blue|B_2) P(B_2)}$

比较两个概率的大小，就可以判别蓝色球更可能来自哪一个盒子。

2. 二分类问题

二分类问题类似于上面的盒子取球问题：将盒 $1$ 、盒 $2$ 视为类别 $1$ 、类别 $2$ ，对于一个待分类的样本 $x$ ，它来自其中某一个类别的概率有多大？

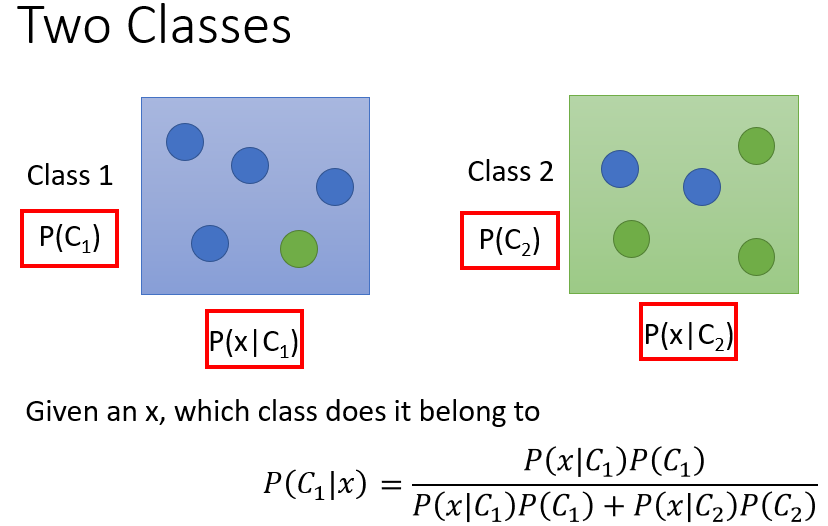
同样地，如果能够得知：

$P(C_1)$ ：选中类别 $1$ 进行抽样的先验概率
$P(x|C_1)$ ：从类别 $1$ 中抽到样本 $x$ 的概率
$P(C_2)$ ：选中类别 $2$ 进行抽样的先验概率
$P(x|C_2)$ ：从类别 $2$ 中抽到样本 $x$ 的概率

就能够计算出样本 $x$ 分别来自类别 $1$ 、类别 $2$ 的概率：

$x$ 来自类别 $1$ 的概率： $P (C_{1} | x) = \frac{P (x | C_{1}) P (C_{1})}{P (x | C_{1}) P (C_{1}) + P (x | C_{2}) P (C_{2})} = \frac{P (C_{1}, x)}{P (x)}$ $P(C_1|x) = \frac{P(x|C_1) P(C_1)}{P(x|C_1) P(C_1) + P(x|C_2) P(C_2)} = \frac{P(C_1,x)}{P(x)}$
$x$ 来自类别 $2$ 的概率： $P (C_{2} | x) = \frac{P (x | C_{2}) P (C_{2})}{P (x | C_{1}) P (C_{1}) + P (x | C_{2}) P (C_{2})} = \frac{P (C_{2}, x)}{P (x)}$ $P(C_2|x) = \frac{P(x|C_2) P(C_2)}{P(x|C_1) P(C_1) + P(x|C_2) P(C_2)} = \frac{P(C_2,x)}{P(x)}$

比较两个概率的大小，就可以判别样本 $x$ 属于哪一类。
因此，在二元分类问题中，我们需要求出上面四个概率，它们的值是通过训练集估测出来的。

这种解决分类问题的思路，属于生成模型（Generative Model）。生成模型是指能够随机生成观测数据的模型，尤其是在给定某些隐含参数的条件下。简单来说，有了这个模型，就可以利用它抽样产生任意一个样本 $x$ ，即可以计算任意一个样本 $x$ 出现的概率：

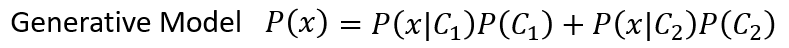
应用实例：对pokemon做分类，从训练集计算各个概率值

分类任务：假设要对pokemon进行分类，只考虑水系（第一类）、一般系（第二类）两类。

数据描述：每只pokemon都用一个向量（vector）来描述，向量中的值代表这只pokemon的各种特征（feature）。所以，vector就是feature，即每个样本向量都是由一堆特征值组成的。

1. 计算先验 $P(C_1)$ 、 $P(C_2)$

将编号ID小于 $400$ 的样本作为训练集，剩余样本作为测试集。
假设训练集的样本分布情况：水系 $79$ 只，一般系 $61$ 只，计算先验 $P(C_1)$ 、 $P(C_2)$

2. 计算条件概率 $P(x|C_1)$ 、 $P(x|C_2)$

训练集中，水系物种有 $79$ 只，其中包含杰尼龟、可达鸭、蚊香蝌蚪等，但是没有出现海龟。

这个时候，若用训练集估测条件概率，就会出现：从水系物种里随机抽一只，抽到海龟的概率等于 $0$ 。但海龟确实属于水系物种，所以这个结果并不合理。

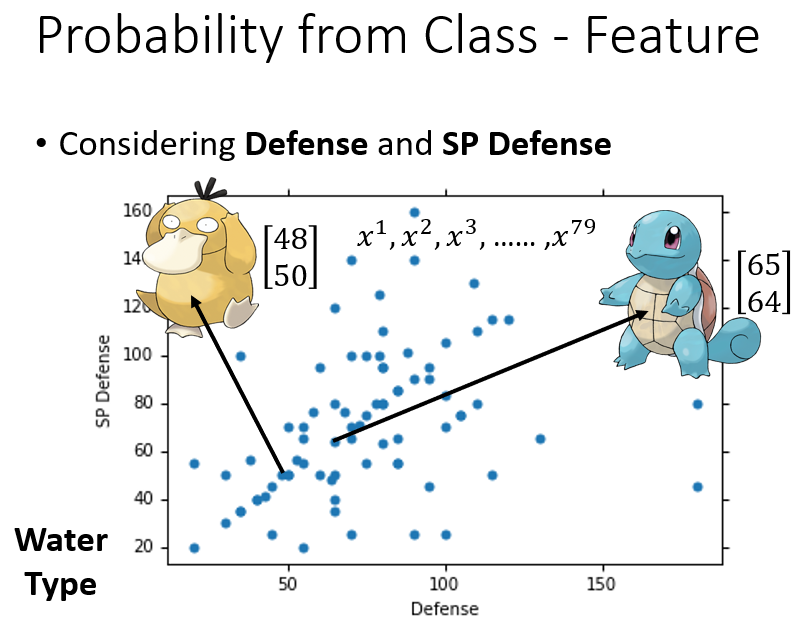
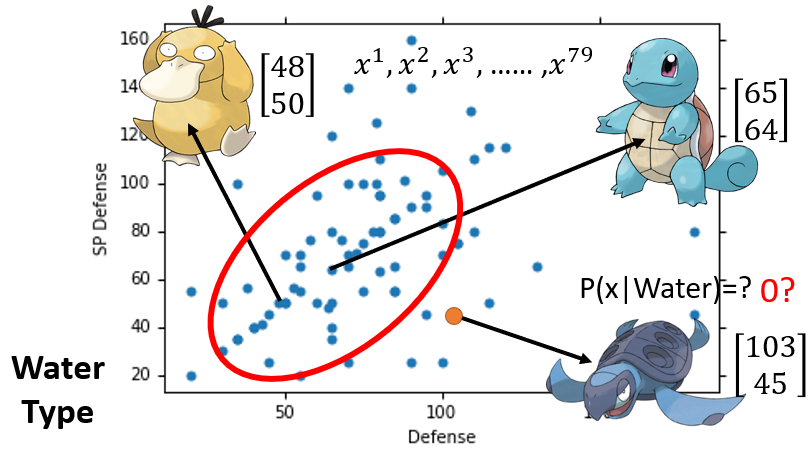
更具体地描述这个问题，假设只考虑pokemon的两个特征：防御力（Defense）和特殊防御力（SP Defense），将训练集的 $79$ 只水系样本 $x^1,...,x^{79}$ 画在坐标图上。例如可达鸭的防御力是 $48$ ，特殊防御力是 $50$ ，代表可达鸭的向量是 $\left[ \begin{matrix} 48 \\ 50 \\ \end{matrix} \right]$ ；杰尼龟的防御力是 $65$ ，特殊防御力是 $64$ ，代表杰尼龟的向量是 $\left[ \begin{matrix} 65 \\ 64 \\ \end{matrix} \right]$ 。

假如给我们一个新的点——海龟，它对应的向量是 $\left[ \begin{matrix} 103 \\ 45 \\ \end{matrix} \right]$ ，而这个点并没有在训练数据中出现过，如果基于训练数据计算样本出现次数作为条件概率值，那么海龟在水系样本中出现次数为 $0$ ，计算出来的条件概率也是 $0$ ，这显然是不对的。

如何从已有的pokemon信息里，估测 $P(杰尼龟|Water)$ 的值？

假设水系物种的所有样本是来自一个多维高斯分布，训练集的 $79$ 只水系样本只是从该高斯分布抽样出来的冰山一角，形成了 $79$ 个样本的分布图。而从最原始的水系物种的高斯分布里抽样，抽到海龟的概率并不是 $0$ 。

我们要做的，就是充分利用已有的 $79$ 个水系样本的信息，找到最佳的多维高斯分布，然后通过这个高斯分布计算抽到海龟的概率。

【多维高斯分布】

多维高斯分布可以简单地视为一个函数，其输入值是一个向量 $x$ ，这里代表某只pokemon的防御力和特殊防御力（二维高斯）。其输出值是从该高斯分布中抽到这只pokemon的概率密度（与抽样概率成正比）。多维高斯分布的两个参数：

均值向量 $\mu$
协方差矩阵 $\Sigma$

多维高斯分布的概率密度函数表示为：

f_{μ, Σ} (x) = \frac{1}{(2 π)^{\frac{K}{2}}} \cdot \frac{1}{| Σ |^{\frac{1}{2}}} \cdot e^{- \frac{1}{2} (x - μ)^{T} Σ^{- 1} (x - μ)}

$f_{\mu, \Sigma}(x) = \frac{1}{(2 \pi)^{\frac{K}{2}}} \cdot \frac{1}{|\Sigma|^{\frac{1}{2}}} \cdot e^{- \frac{1}{2} (x - \mu)^T \Sigma^{-1} (x - \mu)}$ 其中，

K

$K$ 表示向量

x

$x$ 的维度。当参数

μ

$\mu$ 和

Σ

$\Sigma$ 不同时，多维高斯分布的形状也不同。

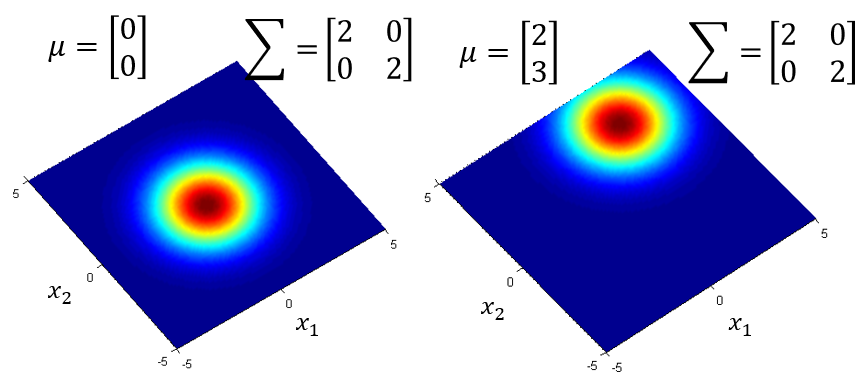
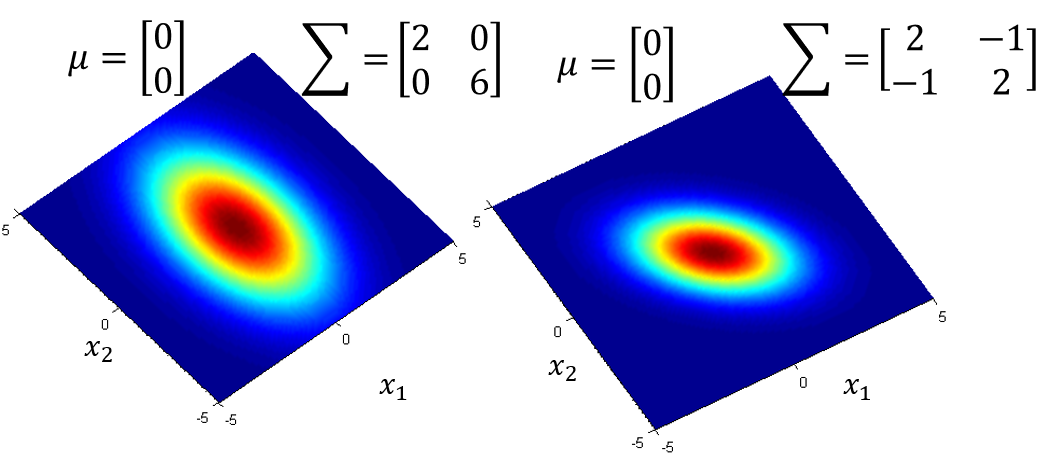
$\mu$ 不同， $\Sigma$ 相同，概率分布图中最高点的位置不同
$\mu$ 相同， $\Sigma$ 不同，概率分布最高点是一样的，但分布离散的程度不同

回到分类问题上，假如 $79$ 个水系样本都来自同一个多维高斯分布，利用样本信息求得最佳参数 $\mu$ 和 $\Sigma$ 后，就可以通过该高斯分布计算新样本出现的概率密度。与一维正态分布类似，新样本越接近均值 $\mu$ ，其出现的概率就越大。

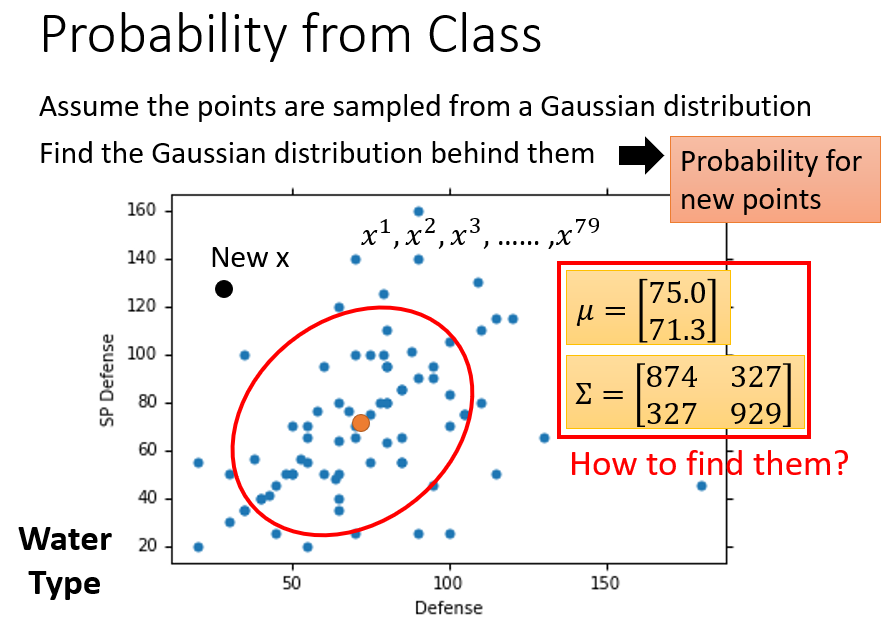
如何确定这个多维高斯分布，或者如何求出这个多维高斯分布的参数 $\mu$ 和 $\Sigma$ ？

事实上，这 $79$ 个样本可以从任何一个多维高斯分布抽样得到，因为多维高斯分布抽样可能抽取到空间上的任何一点，不同高斯抽到同一个点的概率不同，但每一个点被抽到的概率都不会是 $0$ （每个点都有可能被抽到，只是概率大小问题）。例如：

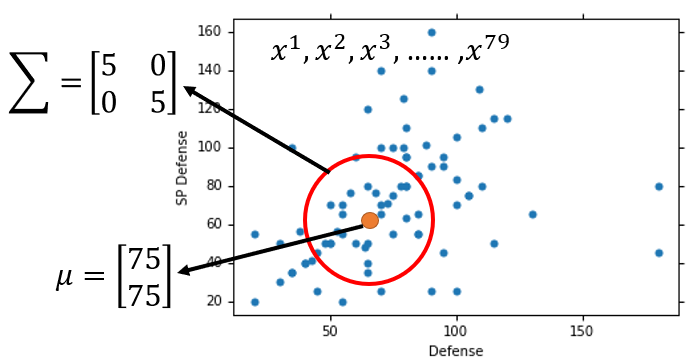
这 $79$ 个样本可能是从 $\mu = \left[ \begin{matrix} 75 \\ 75 \\ \end{matrix} \right]$ ， $\Sigma = \left[ \begin{matrix} 5 & 0 \\ 0 & 5 \\ \end{matrix} \right]$ 这个高斯分布中抽样得到的
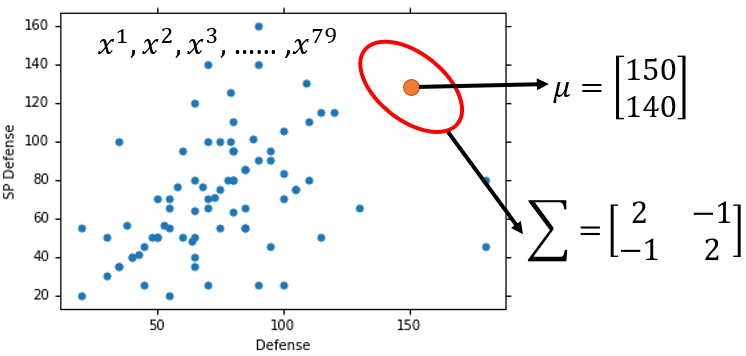
也可能是从 $\mu = \left[ \begin{matrix} 150 \\ 140 \\ \end{matrix} \right]$ ， $\Sigma = \left[ \begin{matrix} 2 & -1 \\ -1 & 2 \\ \end{matrix} \right]$ 这个高斯分布中抽样得到的

虽然两种高斯都可能抽到这 $79$ 个样本，但区别就在于，二者抽到这 $79$ 个样本的概率不同（Different Likelihood）。显然，第一个高斯分布更有可能抽到这些样本（根据样本散点图直观判断）。

随机选取一组参数 $(\mu^{'}, \Sigma^{'})$ ，就可以确定一个多维高斯分布 $f_{\mu^{'},\Sigma^{'}} (x)$ ，从而能够求出在该高斯分布中抽样时，抽到这 $79$ 个样本的概率（似然函数）；再选定另外一组参数 $(\mu^{''}, \Sigma^{''})$ ，也可以求出从 $f_{\mu^{''}, \Sigma^{''}} (x)$ 中抽到这 $79$ 个样本的概率（似然函数）。以此类推，穷举所有的 $\mu$ 和 $\Sigma$ ，每一组参数都能对应求出关于训练集样本的似然函数。

我们要做的就是，找出能够使 $79$ 个样本的似然函数最大（即：使训练集样本出现的可能性最大）的那组参数。

由于每个样本都是独立地从同一个多维高斯分布抽样出来的，所以似然函数表示为各个样本点抽样概率密度的乘积：

L (μ, Σ) = f_{μ, Σ} (x^{1}) f_{μ, Σ} (x^{2}) . . . f_{μ, Σ} (x^{79})

$L(\mu, \Sigma) = f_{\mu,\Sigma}(x^1) f_{\mu,\Sigma}(x^2)...f_{\mu,\Sigma}(x^{79})$

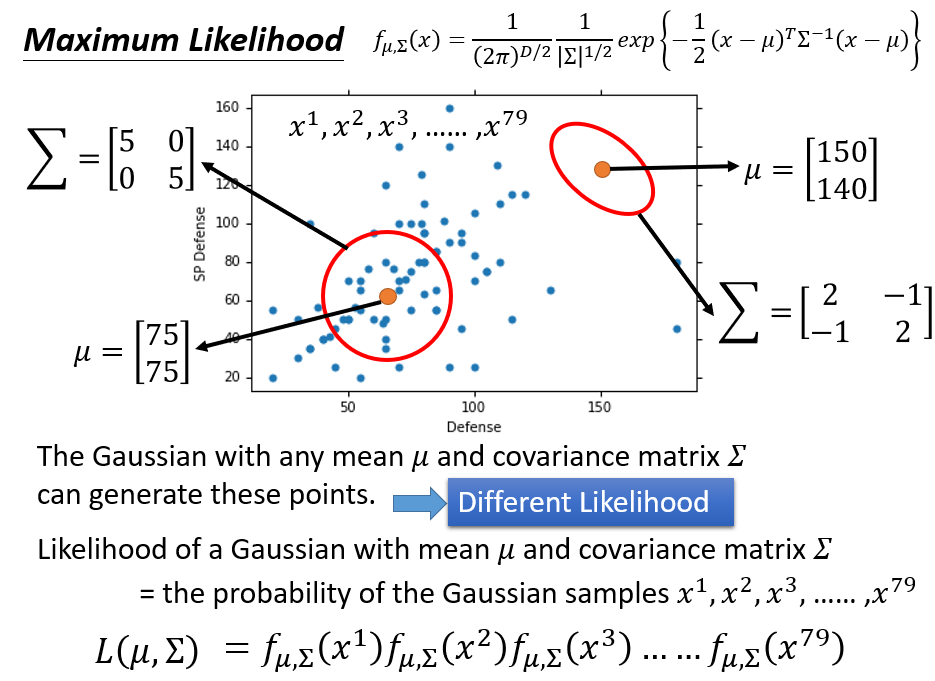
假设使 $79$ 个样本的似然函数最大的一组参数是 $\mu^*$ 、 $\Sigma^*$ ，则用数学表达式写成：

μ^{*}, Σ^{*} = \underset{μ, Σ}{a r g m a x} L (μ, Σ)

$\mu^*,\Sigma^* = \mathop{argmax}_{\mu,\Sigma} L(\mu, \Sigma)$

通过多元正态分布的极大似然估计求得极值点：

μ^{*} = \frac{1}{N} \sum_{n = 1}^{N} x^{n}

$\mu^* = \frac{1}{N} \sum_{n = 1}^{N} x^n$

Σ^{*} = \frac{1}{N} \sum_{n = 1}^{N} (x^{n} - μ^{*}) (x^{n} - μ^{*})^{T}

$\Sigma^* = \frac{1}{N} \sum_{n=1}^{N} (x^n - \mu^*)(x^n - \mu^*)^T$ 其中，

x^{n}

$x^n$ 表示第

n

$n$ 个样本。

依照上述公式：

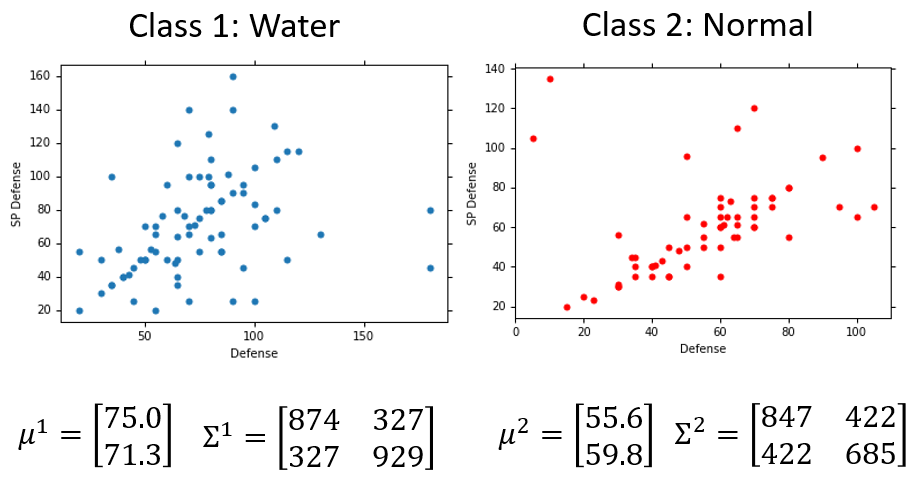
训练集的水系样本有 $79$ 只，可求得多维高斯分布： $\mu^1 = \left[ \begin{matrix} 75.0 \\ 71.3 \\ \end{matrix} \right]，\Sigma^1 = \left[ \begin{matrix} 874 & 327 \\ 327 & 929 \\ \end{matrix} \right]$ ，用这个高斯分布来抽样，抽到这 $79$ 个样本的概率最大。这个高斯分布可以计算 $P(x|C_1)$
训练集的一般系样本有 $61$ 只，可求得多维高斯分布： $\mu^2 = \left[ \begin{matrix} 55.6 \\ 59.8 \\ \end{matrix} \right]，\Sigma^2 = \left[ \begin{matrix} 847 & 422 \\ 422 & 685 \\ \end{matrix} \right]$ ，用这个高斯分布来抽样，抽到这 $61$ 个样本的概率最大。这个高斯分布可以计算 $P(x|C_2)$

如下图横纵轴分别表示防御力、特殊防御力，蓝色点是训练集的水系pokemon的分布，红色点是训练集的一般系pokemon的分布。计算二维坐标图上每一个点 $x$ 属于第一类（水系）的概率 $P(C_1|x)$ ，不同颜色的区域代表 $P(C_1|x)$ 的大小不同：

粉红色区域表示 $P(C_1|x)$ 较大，在这个区域里的点会归入第一类
蓝紫色区域表示 $P(C_1|x)$ 较小，在这个区域里的点会归入第二类

理想情况下，散落在粉红区域内的蓝色样本点应越多越好，说明水系样本被正确地归入第一类；散落在蓝紫色区域内的红色样本点应越多越好，说明一般系样本被正确地归入第二类。

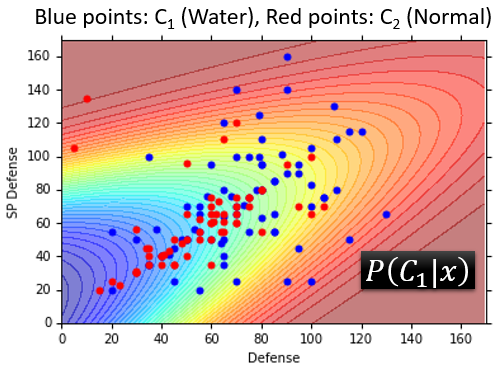
将 $P(C_1|x) = 0.5$ 的分界线表示在坐标图上，更清晰地区分训练集样本的判断结果：蓝色点大多数落在了粉红色区域内，红色点大多数落在了紫色区域内。

进一步地，利用上面求得的两个多维高斯分布： $f_{\mu^1,\Sigma^1} (x)$ 、 $f_{\mu^2,\Sigma^2} (x)$ 计算测试集每一个样本的 $P(C_1|x)$ ，得到的准确率只有 $47$ %。

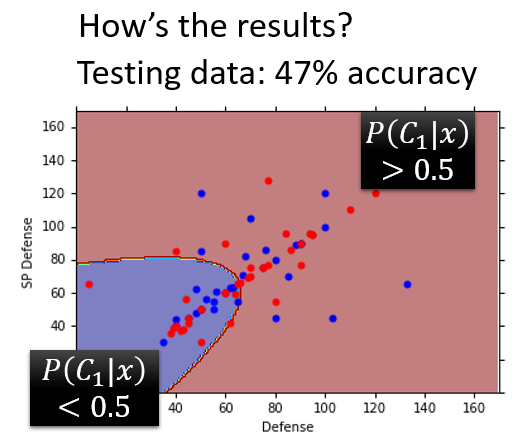
准确率太低有可能是因为考虑的特征比较少，只有两维（防御力、特殊防御力）。机器学习可以处理高维空间的问题，所以考虑 $7$ 个特征：每只pokemon都分布在一个七维空间里，由七个点确定一只pokemon的位置。此时需要重新计算最优高斯分布的参数， $\mu^1,\mu^2$ 都是七维向量， $\Sigma^1,\Sigma^2$ 都是 $7 \times7$ 的对称正定矩阵。再对测试集做预测，得到了 $54$ %的准确率。

后面会继续尝试对概率模型做一些改进。

参考资料：
生成模型与判别模型
 probability principal component analysis