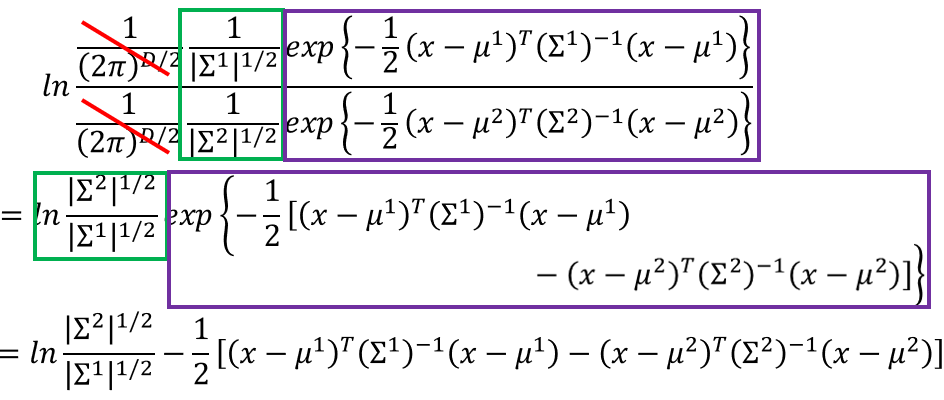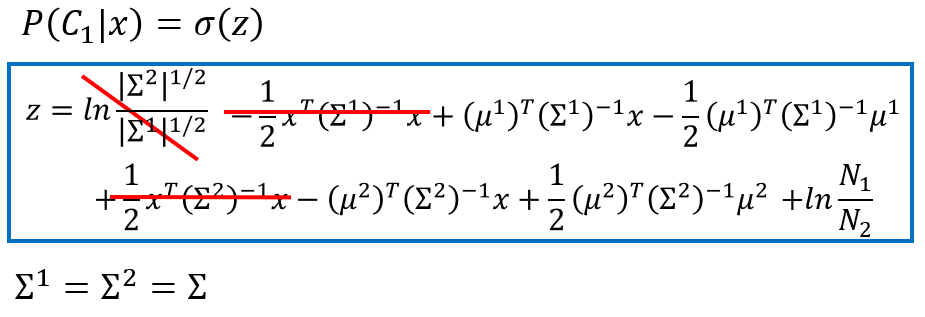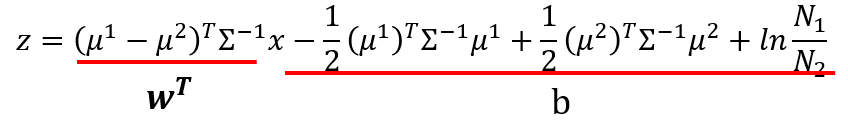ML Lecture 4: Classification——Probabilistic Generative Model
改进分类问题的概率生成模型:共用协方差矩阵
上一节提到,通过建立概率生成模型对pokemon进行分类。概率生成模型中包括两个部分:
- 各类别的先验分布
P(C1)
、
P(C2)
- 每一个类别自身的抽样分布
P(x|C1)
、
P(x|C2)
(假设是高斯分布),有多少个类别就有多少个(高斯)分布

虽然充分利用了样本
7
个特征的信息,准确率仍然只有
54
%。事实上,上节对两个类别分别计算了各自的高斯参数:
水系的多维高斯分布:μ1=[75.071.3],Σ1=[874327327929]
一般系的多维高斯分布:μ2=[55.659.8],Σ2=[847422422685]
可以看到,水系样本原始分布的参数是
(μ1,Σ1)
,一般系样本原始分布的参数是
(μ2,Σ2)
。像这样给不同类别赋予不同的
μ
、
Σ
,在概率生成模型中并不常用。比较常见的做法是,两个类别的高斯分布共用一个协方差矩阵,即令
Σ1=Σ2=Σ
。

这样做的原因是,协方差矩阵里的元素个数与特征维度的平方是成正比的,例如使用
7
个特征时,协方差矩阵就有
49
个元素。随着特征的增多,协方差矩阵内的元素个数增长是十分快的。在这种情况下,如果两个类别分别使用不同的协方差矩阵
Σ1
、
Σ2
,模型的参数就会太多,方差(Variance)就会随之增大,容易造成过拟合。所以为了有效减少参数,可以让水系、一般系的高斯分布共用一个协方差矩阵
Σ
。
如何找到共用的协方差矩阵
Σ
?
第一类有
79
只水系样本,第二类有
61
只一般系样本。当两个类别的高斯分布共用一个协方差矩阵时,不再是“每个类别各自对应一个似然函数”,而是“由一个总的似然函数描述所有样本被抽样的可能性”:
L(μ1,μ2,Σ)=fμ1,Σ(x1)...fμ1,Σ(x79)×fμ2,Σ(x80)...fμ2,Σ(x140)
其中,
fμ1,Σ(x)
为第一个高斯分布,
fμ2,Σ(x)
为第二个高斯分布。
在这种情况下,
μ1
、
μ2
的值与上一节的计算结果完全相同。唯一不同的是,共用的协方差矩阵
Σ
,它是不共用情况下求得
Σ1
、
Σ2
的加权平均:
μ1=179∑n=179xn
μ2=161∑n=80140xn
Σ=79140Σ1+61140Σ2
其中,
Σ1=179∑79n=1(xn−μ1)(xn−μ1)T
,
Σ2=161∑140n=80(xn−μ2)(xn−μ2)T
。

当使用防御力、特殊防御力两个特征:
- 没有共用协方差矩阵的情况下(下左图),分类界线(Boundary)是
P(C1|x)=0.5
的曲线(这种情况下不是线性模型)
- 共用协方差矩阵
Σ
后(下右图),分类界线(Boundary)变成了一条直线。正是由于高斯分布下的分类界线是线性的,所以这样的模型又称为线性模型
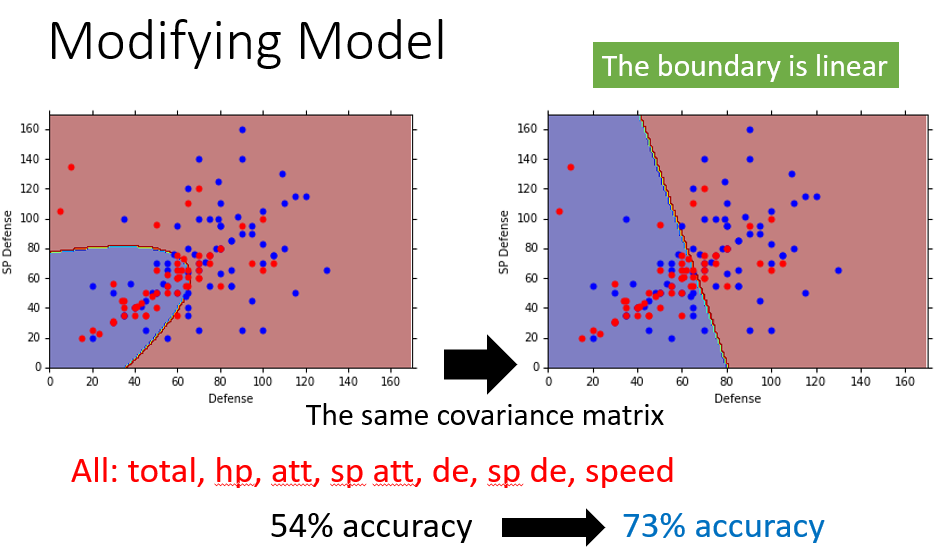
共用协方差矩阵后,考虑所有的
7
个特征,拟合高斯分布,准确率从
54
%上升到
73
%。为什么会出现这么明显的提升呢?这是在高(七)维空间中发生的变化,我们很难直观地认识到分类界线是怎么做切分的(它的形状是怎么样的),所以很难描述准确率提升的原因。但这就是机器学习迷人的地方,虽然人类无法知道怎么做,但机器可以帮助我们做出来。假如只有二维特征,人类可以在二维坐标图上直观地划分类别,也就没有必要使用机器学习。
机器学习三步骤
用概率生成模型解决分类任务,也是分为三个步骤,以二分类问题为例:
第一步,寻找一个模型/函数集
P(C1|x)
,模型中每个函数都包含:第一个类别的先验概率
P(C1)
、第二个类别的先验概率
P(C2)
、第一个类别的抽样概率分布
P(x|C1)
、第二个类别的抽样概率分布
P(x|C2)
。
这些先验概率、概率分布相当于模型的参数,选择不同的概率分布(例如伯努利分布、高斯分布等),就产生不同的参数(伯努利分布的参数
p
、高斯分布的参数
μ
、
Σ
),进而得到不同的函数。这些概率分布不同的函数就构成一个模型/函数集。
分类的判断依据是:若
P(C1|x)>0.5
,
x
就属于第一类;若
P(C1|x)<0.5
,
x
就属于第二类。以上是模型的基本形式。

第二步,评价模型中每一个函数的优劣。假设抽样的概率分布是多维高斯分布,那么就是对不同的参数
μ
、
Σ
做评价。评价参数/函数优劣的依据是:假如一组参数能够使得产生训练样本的概率最大/似然函数最大,那么这组参数/这个函数就是最佳参数/最佳函数。
根据第2步定义的似然函数,找出使似然函数最大的参数
(μ∗,Σ∗)
,从而得到最佳函数
fμ∗,Σ∗(x)
。

对抽样概率分布的假设
在前面的分析中,抽样概率的分布始终是以多维高斯分布为例,即假设不同类别做抽样时的概率分布服从多维高斯分布。实际上,这个概率分布也可以是其他任何可能的分布,是凭人类自己的经验决定哪一个概率模型比较合适,而不是由人工智慧决定的。选择比较简单的概率模型,参数较少,可能出现偏置较大、误差较小的情况;选择比较复杂的概率模型,参数较多,可能出现偏置较小、误差较大的情况。
1. 朴素贝叶斯分类器:对
P(x|C1)
的特征独立假设
我们知道,样本
x
是一个向量,它由一组特征值描述,有几个特征,
x
就是几维的。例如在pokemon分类问题中,由
7
个特征构成一只独一无二的pokemon,那么这只pokemon就是一个
7
维的向量。
有一种常见的假设:假设每一维特征从概率模型中产生的概率,都是相互独立的。那么一个样本被抽到的概率,就等于它的各个特征被单独抽到的概率的乘积。
例如在pokemon分类问题中,从第一个类别里抽到一只生命值
150
、防御力
65
、特殊防御力
45
的pokemon的概率,就等于从第一个类别里抽到生命值为
150
的pokemon的概率,乘以从第一个类别里抽到防御力为
65
的pokemon的概率,再乘以从第一个类别里抽到特殊防御力为
45
的pokemon的概率,是三个概率的乘积。即:
P(x=⎡⎣⎢x1=150x2=65x3=45⎤⎦⎥|C1)=P(x1=150|C1)⋅P(x2=65|C1)⋅P(x3=45|C1)
推广到多维特征的情况,若样本
x=⎡⎣⎢⎢⎢⎢⎢⎢x1...xk...xK⎤⎦⎥⎥⎥⎥⎥⎥
,概率分布可以表示为:
P(x|C1)=P(x1|C1)...P(xk|C1)...P(xK|C1)
若假设这些抽样概率分布是高斯分布,那么
P(x1|C1)
、…、
P(xk|C1)
、…、
P(xK|C1)
都是一维高斯分布,因为每一个概率分布只含有一个(维)特征。在这个假设下,多维高斯分布
P(x|C1)
,其协方差矩阵变成一个
对角矩阵(Diagonal Matrix),非对角位置的元素全部为
0
,所以能有效减少参数量,获得更简单的模型。

【注】:
P(x1|C1)
、…、
P(xk|C1)
、…、
P(xK|C1)
不一定必须是高斯分布,当特征
xk(k=1,2,...,K)
是诸如战斗力、生命力、抵抗力等连续变量时,可以假设是高斯分布。但当特征
xk(k=1,2,...,K)
是二分类的离散变量,例如pokemon是/不是神兽,很明显这个不是高斯分布,而更有可能是伯努利分布。

基于以上特征/维度独立假设(不考虑特征/维度之间的协方差)的概率生成模型称为朴素贝叶斯分类器(Naive Bayes Classifier)。之所以称之为朴素(Naive)的贝叶斯,就是因为其简化了很多条件,进行了最直接暴力的假设,如果“假设各个特征/维度相互独立”这件事是符合实际的,那么朴素贝叶斯分类器可以带来很好的分类效果。
但也由于模型过于简单,忽略了许多内在关系,当假设不成立时,分类结果的误差很大。例如在pokemon的分类问题上,分类结果就十分不理想。因为它假设一只pokemon的各个特征之间是相互独立的,就像假设一个人的身高与体重之间没有关系一样,都是不合理的。

2. 后验概率与Sigmoid函数:
P(C1|x)=σ(z)=11+e−z
接下来我们需要分析后验概率:
P(C1|x)=P(x|C1)P(C1)P(x|C1)P(C1)+P(x|C2)P(C2)=11+P(x|C2)P(C2)P(x|C1)P(C1)
令
z=lnP(x|C1)P(C1)P(x|C2)P(C2)
,则后验概率可以表示为:
P(C1|x)=11+e−z=σ(z)
σ(z)
又称为
Sigmoid函数。当
z→+∞
时,
σ(z)→1
;当
z→−∞
时,
σ(z)→0
。它的形状如下:

【Warning of Math】
σ(z)
是一个关于
z
的函数,而
z
取决于
P(x|C1)
、
P(x|C2)
的概率分布。
假设
P(x|C1)
、
P(x|C2)
都是多维高斯分布,那么
z
的表达式是怎样的?

已知:
z=lnP(x|C1)P(C1)P(x|C2)P(C2)=lnP(x|C1)P(x|C2)+lnP(C1)P(C2)
其中,
P(C1)P(C2)=N1N1+N2N2N1+N2=N1N2
。
N1
是第一个类别的样本数量,
N2
是第二个类别的样本数量。
假设
P(x|C1)
、
P(x|C2)
服从
K
维高斯分布,则:
P(x|C1)=1(2π)K2⋅1|Σ1|12⋅e−12(x−μ1)T(Σ1)−1(x−μ1)
P(x|C2)=1(2π)K2⋅1|Σ2|12⋅e−12(x−μ2)T(Σ2)−1(x−μ2)
P(x|C1)P(x|C2)=|Σ2|12|Σ1|12⋅e−12[(x−μ1)T(Σ1)−1(x−μ1)−(x−μ2)T(Σ2)−1(x−μ2)]
所以有:
lnP(x|C1)P(x|C2)=ln|Σ2|12|Σ1|12−12[(x−μ1)T(Σ1)−1(x−μ1)−(x−μ2)T(Σ2)−1(x−μ2)]
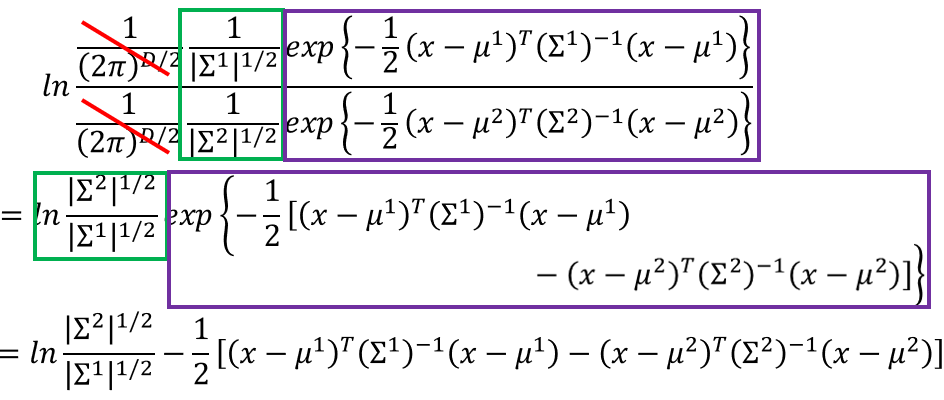
其中:
(x−μ1)T(Σ1)−1(x−μ1)=xT(Σ1)−1x−2(μ1)T(Σ1)−1x+(μ1)T(Σ1)−1μ1
(x−μ2)T(Σ2)−1(x−μ2)=xT(Σ2)−1x−2(μ2)T(Σ2)−1x+(μ2)T(Σ2)−1μ2

将
lnP(x|C1)P(x|C2)
、
lnP(C1)P(C2)
代入
z
中整理得:
z=ln|Σ2|12|Σ1|12−12xT(Σ1)−1x+(μ1)T(Σ1)−1x−12(μ1)T(Σ1)−1μ1+12xT(Σ2)−1x−(μ2)T(Σ2)−1x+12(μ2)T(Σ2)−1μ2+lnN1N2
在共用协方差矩阵的情况下,
Σ1=Σ2=Σ
。则
z
的表达式简化为:
z=(μ1−μ2)TΣ−1x−12(μ1)TΣ−1μ1+12(μ2)TΣ−1μ2+lnN1N2
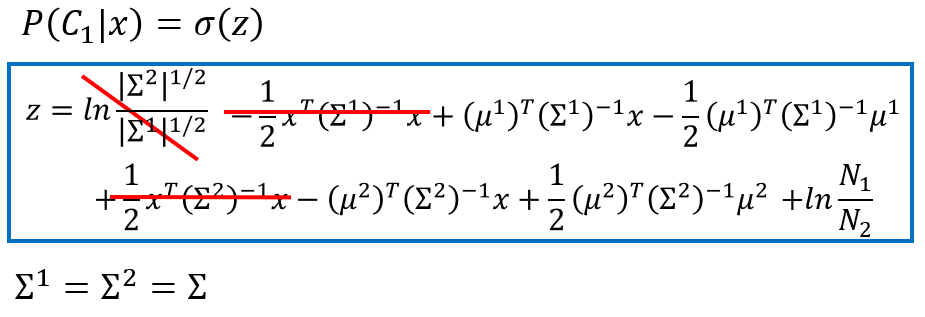
记
wT=(μ1−μ2)TΣ−1
,则
w
是一个
K×1
的列向量,
wTx
是一个数值;记
b=−12(μ1)TΣ−1μ1+12(μ2)TΣ−1μ2+lnN1N2
,
b
是一个数值。则
z
又可写为线性形式:
z=wTx+b
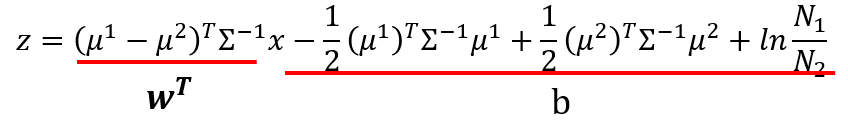
综上,后验概率表示为:
P(C1|x)=11+e−z=σ(z)=σ(wTx+b)
。注意到,结果之所以能表达为线性形式,就是因为假设两个类别的高斯分布共用一个协方差矩阵
Σ
。这也解释了为什么在高斯分布(共用协方差矩阵)的假设下,分类界线(Boundary)是一条线性的直线。
Logistic回归:直接寻找二分类模型的参数
w
和
b
按照前面的分类思想,二分类问题中,后验概率
P(C1|x)
有两种计算思路:
假定
P(x|C1)
、
P(x|C2)
分别服从
K
维高斯分布
NK(μ1,Σ)
和
NK(μ2,Σ)
,它们共用一个协方差矩阵
Σ
。
已知:
P(C1|x)=P(x|C1)P(C1)P(x|C1)P(C1)+P(x|C2)P(C2)
则可以通过极大似然估计求解参数:
μ1
(
K×1
)、
μ2
(
K×1
)、
Σ
(
K×K
)
进而计算:
向量wT=(μ1−μ2)TΣ−1
常数b=−12(μ1)TΣ−1μ1+12(μ2)TΣ−1μ2+lnN1N2
这种方法建立的模型称为概率生成模型,因为我们求出了每一个分布的参数,从而能够计算新样本出现的概率。

由于
P(C1|x)=σ(wTx+b)
,而我们的目标只需要求出一个向量
w
和一个常数
b
,那么另一种思路就是,不去求
μ1
、
μ2
、
Σ
,而是通过梯度下降法直接求解参数
w
、
b
。
这种方法建立的模型称为判别模型。
下面探讨用第二种方法:分类问题中的判别模型——Logistic回归,梯度下降法求出参数
w
和
b
。

参考资料:
维基百科:多元正态分布