ML Lecture 1: Regression - Case Study
Regression(回归):输出数值
之前提到,机器学习要做的事情就是寻找函数,而回归要做的事情就是使我们所找的那个函数,其输出为数值型。或者说,如果我们找到的函数,它的输出是数值型的,这类型的任务就称为回归。举几个关于回归的例子:
- 股票市场的预测:找一个函数,其输入是过去股票市场的变动情况,输出是明天道琼工业指数的数值
- 驾驶无人车:找一个复杂函数,其输入是无人车上的各个感受器收集的数据,输出是方向盘角度
- Amazon的商品推荐/Youtube的视频推荐:找一个函数,其输入是用户A、商品B的各种特性,输出是用户A购买商品B的可能性
应用实例:做回归,预测pokemon进化后的CP值(战斗力)
回归任务:找一个函数,其输入用
来表示,代表pokemon进化前的各种指标(例如:进化前的CP值
、所属物种
、进化前的HP值
、重量
、高度
等),输出是进化后的CP值,用
来表示。

如何找出这个函数?之前提到,机器学习的三个步骤分别是:
第一步,寻找一个模型(即一组函数/一个函数集)。假设我们认为进化后的CP值 与进化前的CP值 有密切的关系,那么就可以将模型表示为:
并称之为线性模型(Linear Model),这个模型随着参数 和 取不同值,可以形成多个函数 。显然,该模型(函数集)中的函数并非全部是合理的,我们需要从中挑取有利于预测的函数。进一步地,考虑其他的各种指标,可以将模型推广表示为:其中, 泛指各种指标/特征(Feature): ; 称为权重(Weight); 称为偏置(Bias)。
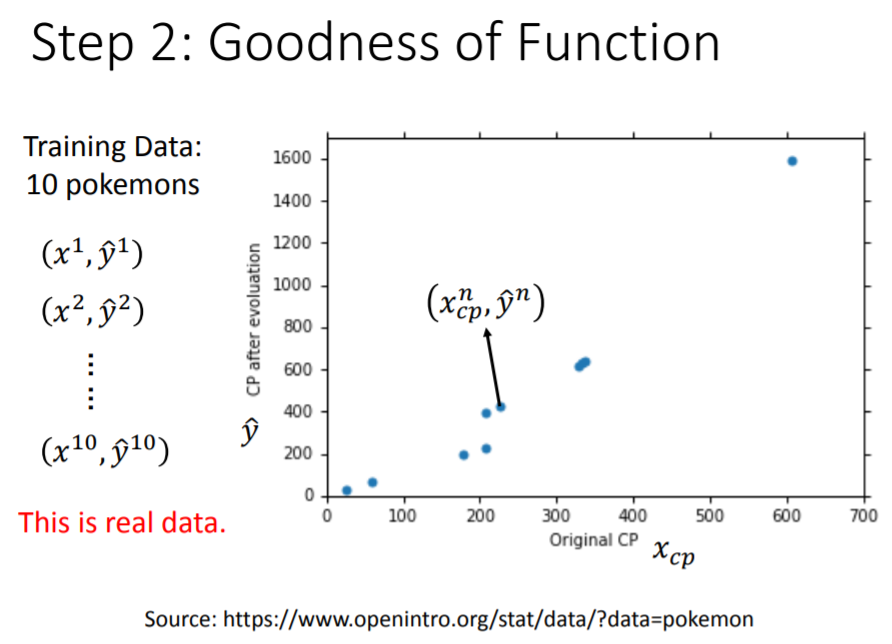
第二步,判断函数的优劣。为此,我们必须收集一些训练资料,其中包括不同pokemon的 。其中 代表第 只pokemon进化前的CP值, 代表第 只pokemon进化后的真实CP值。下图是收集到 只pokemon的训练资料(蓝色点):
有了数据以后,就可以考察模型中的任意一个函数的优劣,这种“评价”是通过定义另一个函数,即
损失函数(Loss Function)来完成的,通常用 表示。注意,损失函数是关于 的函数,即函数的函数。它的输入是:模型中的任意一个函数 (由参数 和 决定);输出是:关于这个函数优劣的评价。
统计学习常用的损失函数有:0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等,这里采用最常见的平方损失函数:
第三步,根据定义的损失函数 ,按照 越小越好(即损失越少越好)的原则,从模型中挑选最佳函数 ,这个过程用公式表示为:
寻找 就是寻找最佳参数 。一个有效方法是
梯度下降法(Gradient Descent),只要损失函数 是可微分的,都可以用此方法求解最佳函数/参数: 。
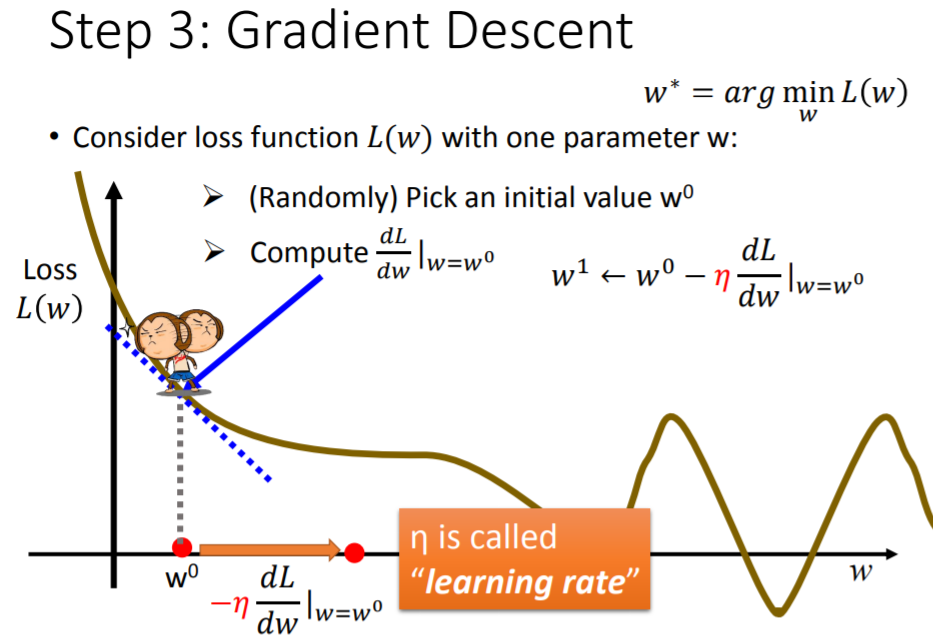
梯度下降法是如何工作的呢?首先不考虑 ,假设待求解的参数只有 ,再定义一个关于 的损失函数 ,这个 可以是任何形式的函数,只要满足:可微分、能够衡量 的优劣。有了 后,我们要做的就是找一个 ,使得 最小。最容易联想到的做法就是暴力穷举所有 ,逐个代入 ,比较之后得到最小的 ,然而此举效率十分低下。
采用梯度下降法可以克服上述困难:它不是穷举所有 ,而是首先随机选取一个初始 ,计算 在 处的导数: ,得到的数值即损失函数的曲线在 处的切线斜率:- 若 ,说明 的曲线正在下降,应该增大 ,以降低
- 若
,说明
的曲线正在上升,应该减小
,以降低
增大或减小的幅度取决于两件事:
- 当前导数值 的大小。它代表了损失函数的曲线当前正处于陡峭,还是平坦状态。显然,在曲线越陡峭的位置, 稍微增大或减小一点,就会使损失函数发生很大的变动
学习率(Learning Rate)的大小。 是自行设定的常数项,它决定了参数学习速度有多快。 越大,则 下一步要跨越的距离就越大(即参数更新的幅度大),意味着参数的学习效率比较高
注意,由于导数值 的正负与 的移动方向恰好相反,所以 更新时,应该加上负号,即 。按照这样的规则,从初始参数开始迭代: 。
在针对线性回归的迭代过程中,参数的更新使得损失函数不断下降,最终逼近最优参数 ,使损失函数取得最小值。梯度下降法之所以能用来解决线性回归任务的参数求解,是因为这里的损失函数 是一个凸函数(Convex Function),其中不存在局部最小值的问题,最后只有一个全局最小值,所得即所求。
事实上其他许多参数求解问题,虽然每一次更新也使损失函数不断下降,但最后到达的是局部最小值(Local Minimum)。此时,损失函数看似到达最低点,并且由于导数值 ,参数会停止更新。但在整个损失函数中,可能存在着一个更低点全局最小值(Global Minimum),而全局最小值才是我们的终极目标。关于这一点,后面会作图解释。
同理,当有两个参数 时,首先定义一个关于 的损失函数 ,然后随机选取一组初始参数 ,计算在 处, 对 和 的偏导数: , 。
按照 , ,进行两个参数的迭代更新,直到最后偏导数等于 ,参数停止更新。此时的参数 能够使损失函数最小。
梯度下降中的梯度,就是指损失函数 对各个参数求偏导后,所组成的向量:
上述关于两个参数的迭代过程,可以理解如下:图中每一个点分别代表不同的 ,越往中间(紫色部分),损失函数的值越小,对 的每一次更新,都是沿着等高线的法线方向,往中间地区移动。
同样地,可以推广到用梯度下降法求解多个参数的情形。假设 表示一个参数的集合,运用梯度下降法求解时,我们希望参数的每一次更新,都能使损失函数再降低一点:
但正如前面所说,梯度下降法的缺陷在于:
选取不同的初始参数,可能会得到不同的局部最小值
在全局/局部最小值处,参数不再更新,是因为这里的导数值为 。但其实在整个
误差曲面(Error Surface)上,导数值为 的点不止全局/局部最小值,也有可能是鞍点(Saddle Point)。鞍点的位置如下图浅蓝色框所示,在该点处,导数值为 却并非最小值点在实际迭代操作中,我们往往不会真的等到导数值为 ,才停止参数的更新,而是会设定一个
阈值(Threshold),当导数值小于此阈值时,我们就认为损失函数已经差不多接近最小值,参数也差不多接近最优,并停止迭代。但这样的做法会带来问题:绿色框对应的点,其实离全局/局部最小值、鞍点还很远,但由于处在非常平坦的地方,其计算出来的导数值特别小,每一次参数更新都只前进一点点,若此时误以为已经接近目标而停止迭代,那么求出来的参数是无法使损失函数最小的
必须强调的是,在线性回归模型中,由于损失函数是一个凸函数,类似于碗的形状,不存在多个最小值,因此从任何一个初始位置出发,最后都会回到唯一的最低点,所以能够克服上述缺陷。
模型选择与评估
至此,关于如何用梯度下降法求解回归方程参数的基本原理就结束了,下面开始运用实际数据做拟合。以 只pokemon的基本信息(每个样本的指标 及其对应的输出 )作为训练集,考虑到进化后的CP值 应该与进化前的CP值 值有密切联系,因此尝试拟合第一个模型:
计算两个偏导数:
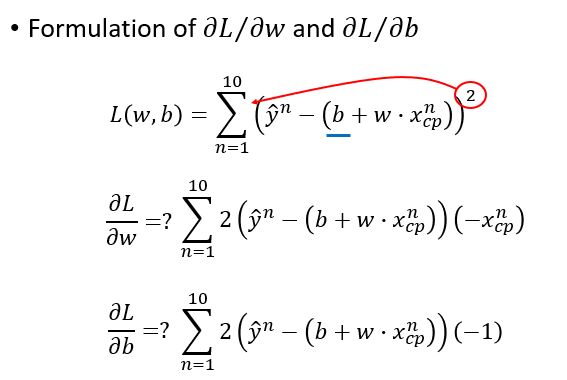
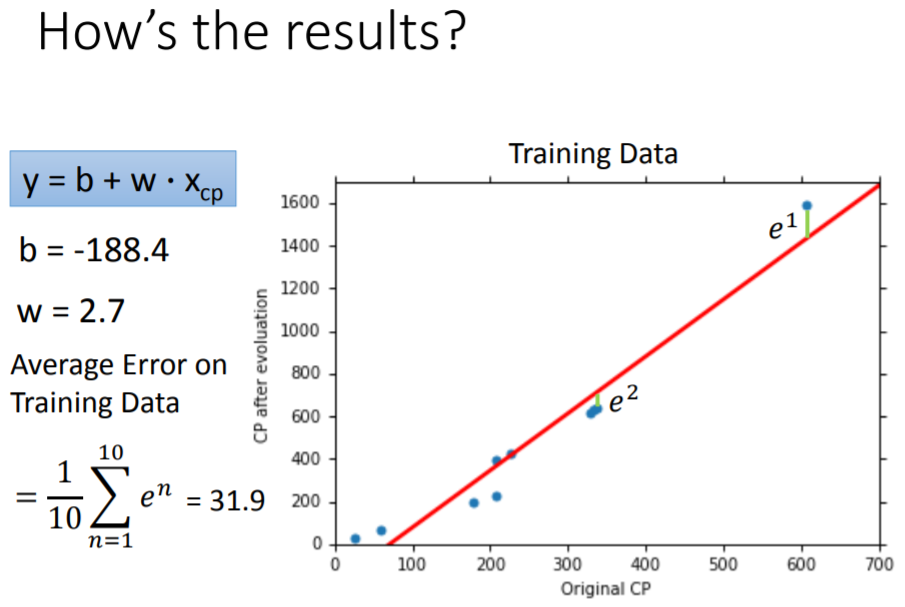
假设在第一个模型上,通过训练集的数据资料,迭代求得最优参数为
。于是我们得到的最优函数为:
,这个函数基于训练集的平均误差为
。平均误差(Average Error)的计算公式为:
再抓取
只新的pokemon的基本信息(新样本的指标
及其对应的输出
)作为测试集,对函数的泛化性能作一评估,得到测试集上的平均误差为
。
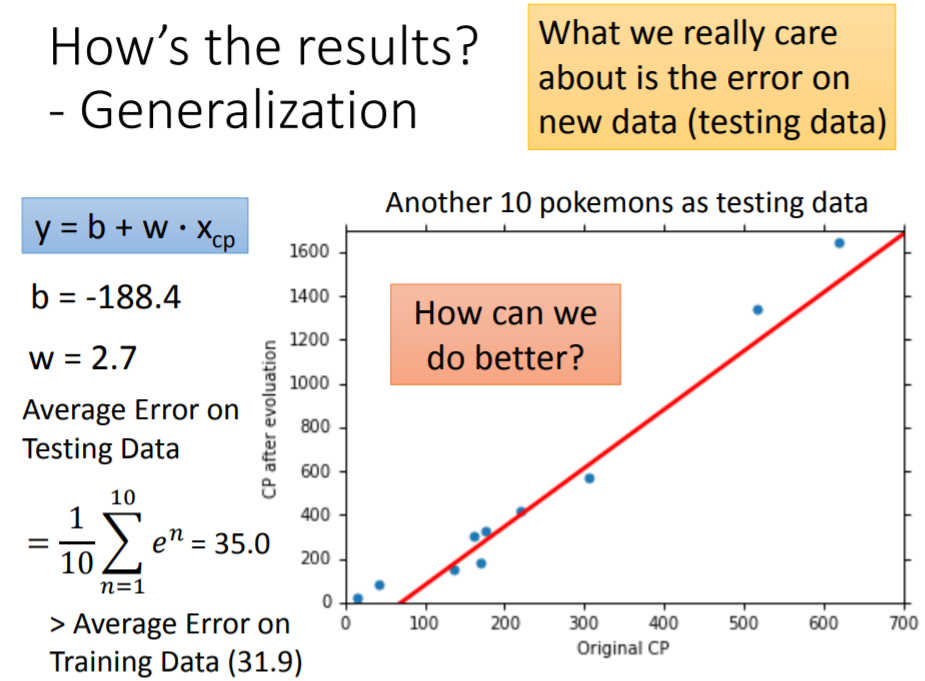
考虑进化后的CP值 与进化前的CP值 、及其平方项 之间的关系,拟合第二个模型:
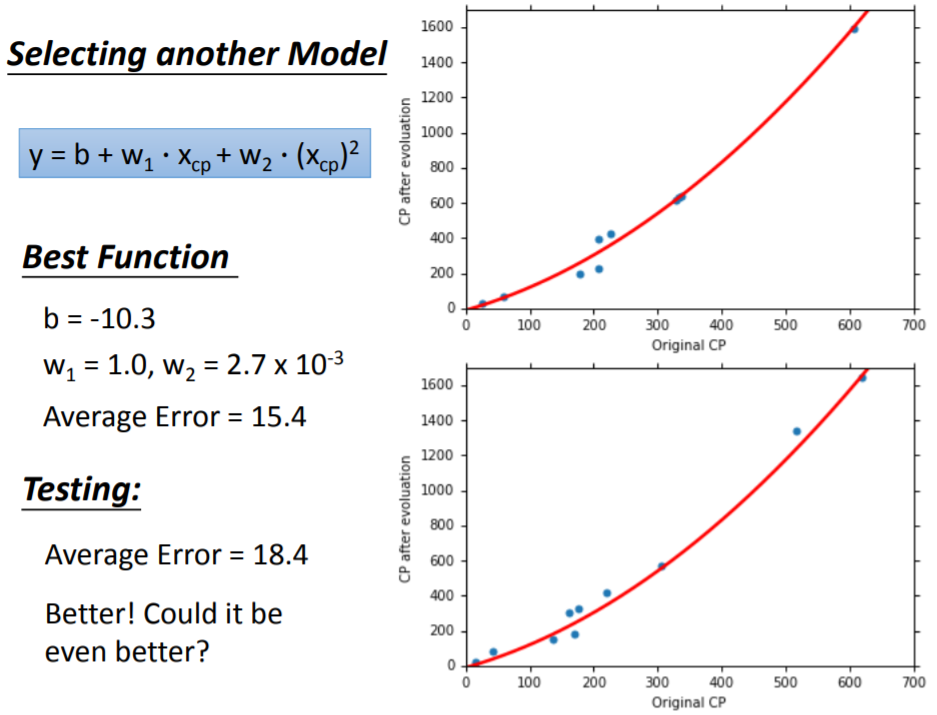
以此类推,考虑 、平方项 、三次方项 ,拟合第三个模型:

当拟合第四个模型:
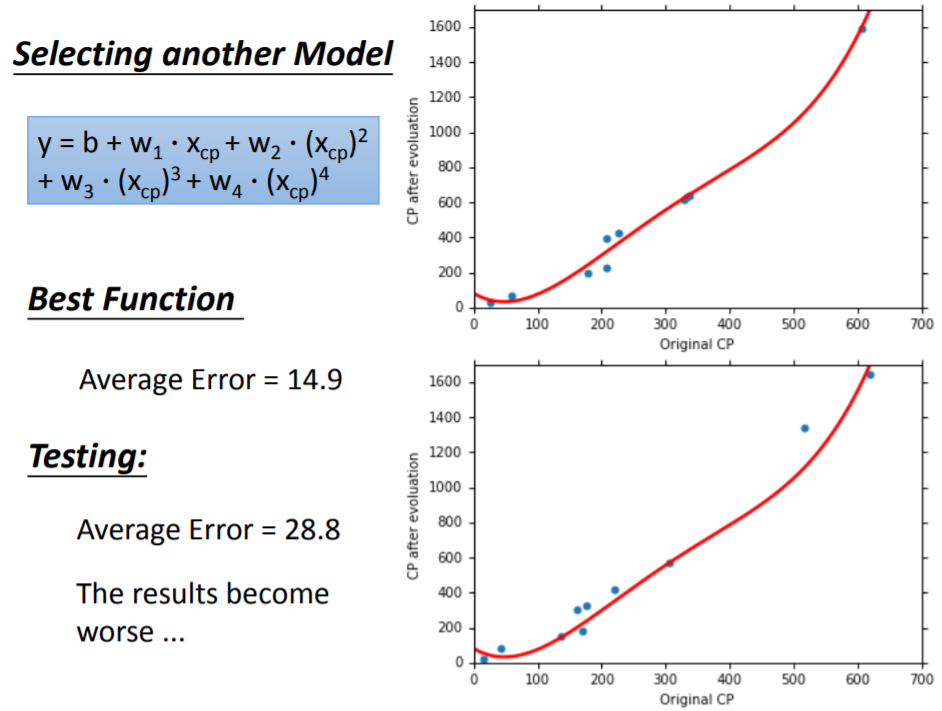
当拟合第五个模型:

【注】:上述拟合的五个模型都是线性的,因为模型是相对于参数 和 而言的, 、 、 …则视为不同的样本特征(feature),可以用 、 、 代替。
从第一个模型到第五个模型,易观察到,随着模型越来越复杂,基于训练集所求出来的平均误差是越低的,而基于测试集的平均误差则是先减小后增大,出现了过拟合问题。为什么会出现过拟合?考察上面五个模型(函数集)之间的关系,它们之间满足:

而在测试集上,第三个模型的性能是最好的,从第四个模型开始,平均误差逐渐增大。可见,并不是越复杂的模型就越好,它在测试集上的性能并非一直提升。一个复杂模型在训练集上得到了比较好的性能,而在测试集上性能表现十分不理想,这就是过拟合(Overfitting)问题。事实上,我们更关注的是模型在测试集(而非训练集)上的表现,因此在模型选择过程中,应该以在测试集上表现最佳的模型作为最终选择。

解决过拟合的其中一个方法是收集更多的数据。当持有更多数据的时候,会发现进化后的CP值
并不只与进化前的CP值
有关,还与pokemon的物种有关。
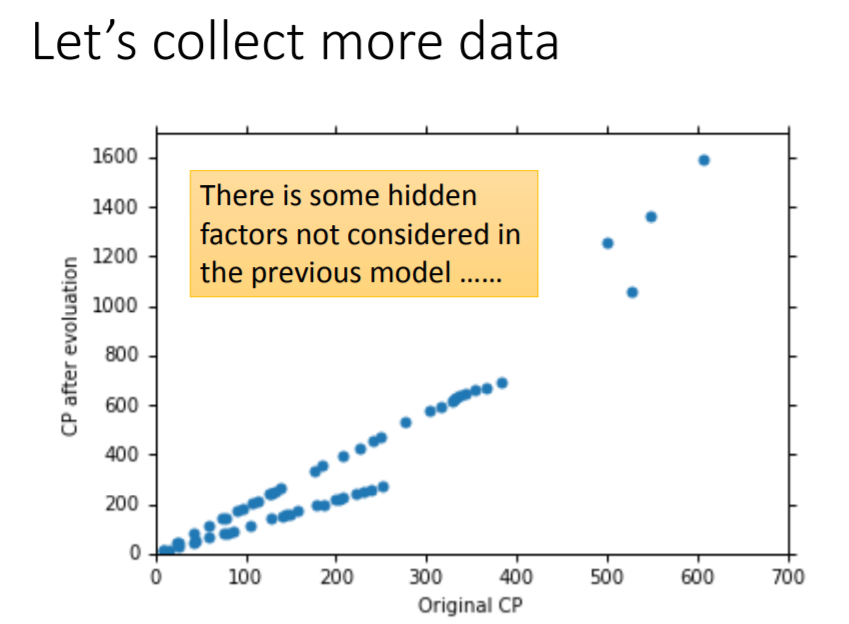

因此重新设计模型,加入
,代表pokemon的种类。当
取不同的值,分别对应不同的函数表达式。这样的模型仍然是一个线性模型:
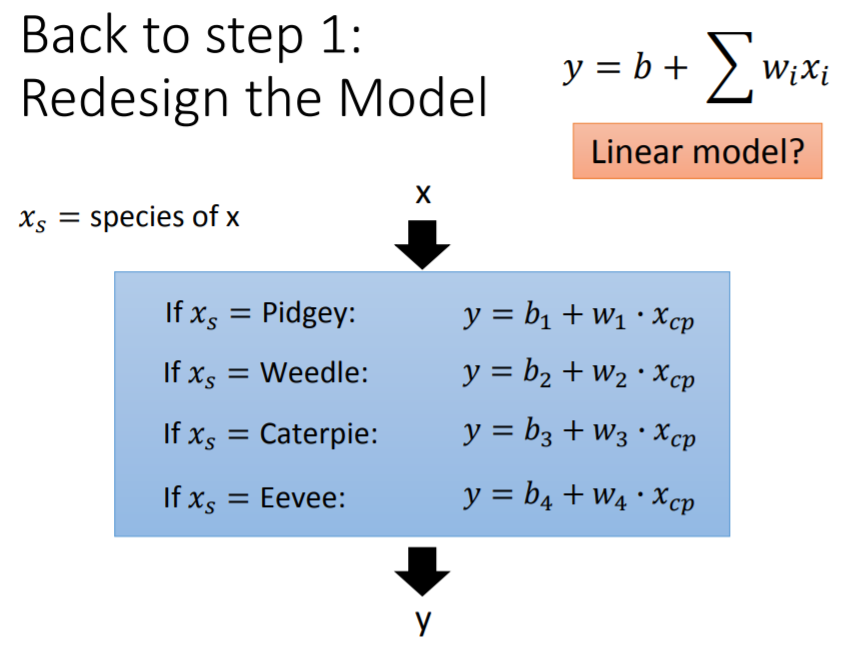
上述线性模型引入
(相当于哑变量)后,可进一步表示为:

其中,蓝色方框内的
个变量可视为
,
则视为
个参数,因此该模型仍然是一个线性模型。用此模型在训练集上拟合,可求得
个参数,代表四条曲线,分别反映四个物种的进化情况:蓝色是波波(Pidgey),绿色是绿毛虫(Caterpie),黄色是独角虫(Weedle),红色是伊布(Eevee)。图中由于绿毛虫与独角虫的直线重合,所以看上去只有三条。最后,在训练集上平均误差为
,在测试集上平均误差为
。
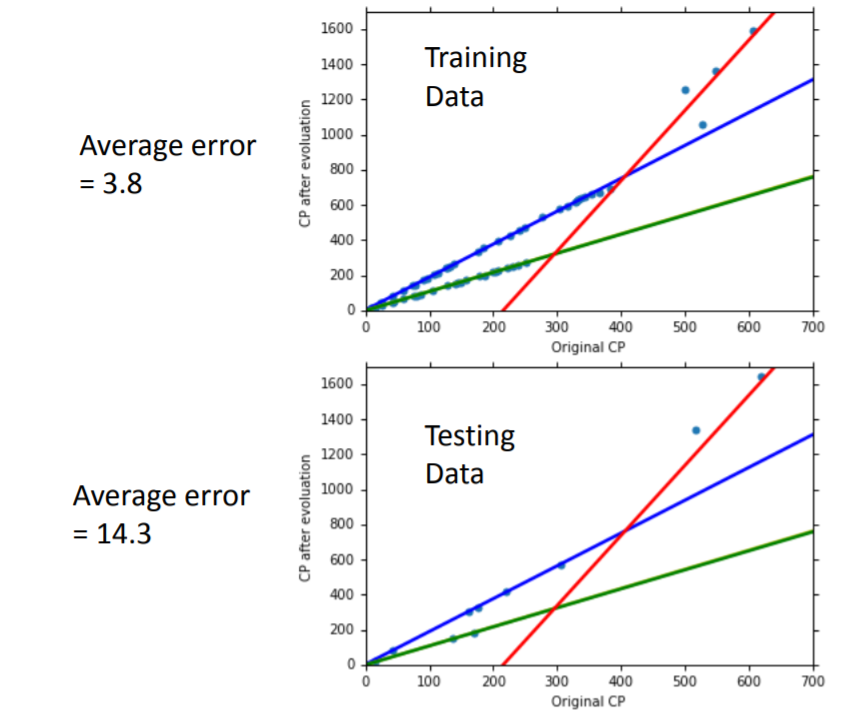
考虑物种后,尽管模型性能进一步提升,但在训练集上的平均误差还是没有接近
,这可能是由于直线不足以描述
与
之间的关系,又或者是还有其他相关的因素未加以考虑:例如观察散点图,认为pokemon的HP值可能与进化后的CP值存在一定的关系。
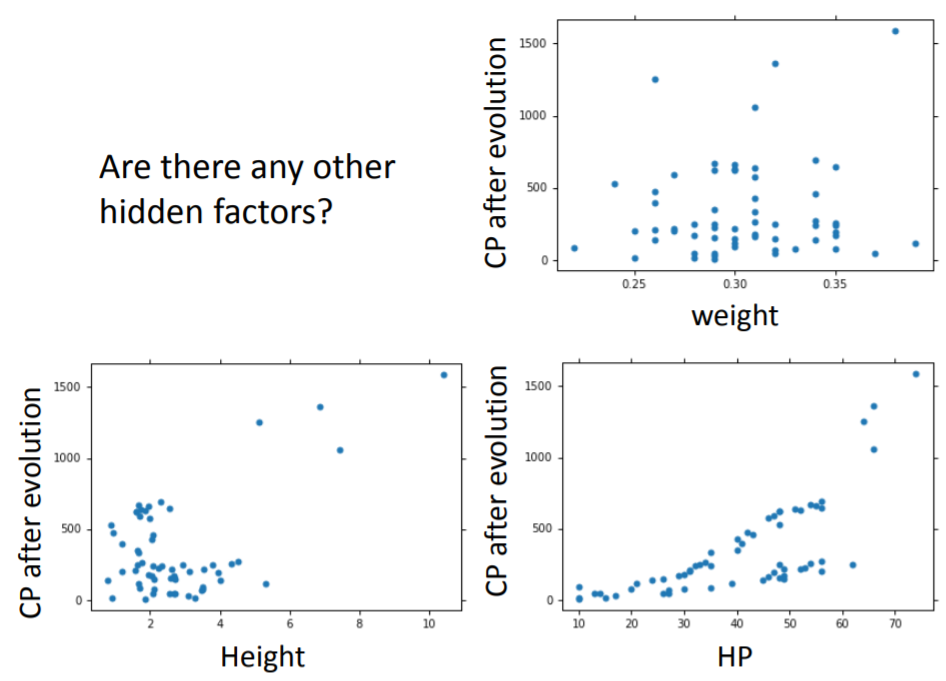
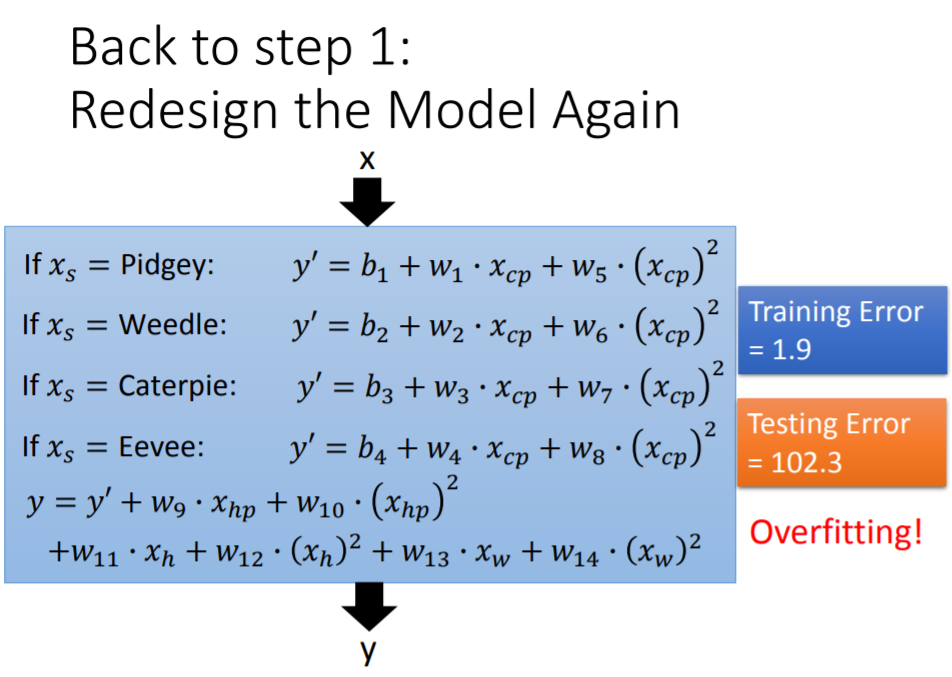
因此,在考虑物种因素的模型基础上,尝试加入:进化前的CP值的平方项
、体重
、高度
、HP值
,构成了含有
个参数(
)的新模型。最后得到训练集上的平均误差为
,测试集上的平均误差高达
,出现严重过拟合,说明上述尝试并不能改进模型。
防止过拟合:正则化
以往我们定义损失函数后,就按照使训练集的损失函数最小化/平均误差最小化的原则求取参数,并得到最佳的预测函数 。但通过这种方法得到的函数,可能是过拟合的,导致在测试集上的预测结果有时并不理想。
针对上一节的过拟合问题,如果具备相应的领域知识(Domain Knowledge),那么可以根据专业知识删除一些不重要的因素。但在无法对各个因素做出准确判断的情况下,通常采正则化(Regularization)来防止过拟合。
正则化方法对损失函数进行了重新定义,在原有损失函数的基础上,加入了一个正则项。假设线性模型为:
正则项 是由 和所有参数 的平方和构成的。定义新的损失函数后,求 意味着同时求 和 :即它不仅要求原有的损失函数 最小化,还要求正则项也最小化。
使损失函数 最小化容易理解。但最小化正则项对于模型选择有什么帮助呢?或者说,加入正则项的意义是什么?
首先明确,在模型
中,参数
很小意味着模型里的函数是比较平滑的。所谓函数平滑(Smooth),是指当输入值
发生变化时,这种变化不会引起输出值
的剧烈变动,即
越小,
对
的影响越小(可以理解为较小的
,降低了
变化带来的冲击)。举个极端例子,当
,
是一条相当平滑的直线,
的任何变化都不会对
造成影响。
因此,正则项最小化意味着我们寻找的最佳函数,要尽可能的平滑,能够最大程度地抵挡因输入值变化而对输出值带来的冲击。
而正则项的意义就在于:当我们从一个模型(函数集)中挑选最佳函数 时,正则项的存在能够防止我们挑到对波动十分敏感的函数。加入正则项,使 尽可能平滑的做法之所以成立,是因为“在多数状况下,我们认为平滑曲线更有可能是正确的目标函数,更有利于预测,波动幅度很大的函数往往会造成很大的误差”。
然而,正则项也有失灵的时候。正则项的存在是为了使挑出来的预测函数 更平滑,减小测试集上的误差。但,假如真实的函数本身就是一个波动性很大的函数,我们还利用正则项去挑选平滑的预测函数,那么与真实函数是背道而驰的。不过一般情况下,还是认为正确的函数不会长得很奇怪,不会波动特别厉害,所以正则项还是颇有帮助。
总而言之,新的损失函数 由于加入了正则项,令我们的目标变成了:
- 寻找最佳函数 ,使得原来的损失函数 是最小的
- 这个最佳函数 自身的参数 也是尽可能小的,从而使 尽可能地平滑
对于正则项,还有两个需要注意的地方:
- 正则项中还有一个常数 ,它是一个需要手动设置的参数,决定了 的平滑程度( 越大,则要求 越平滑)
- 通常只对权重参数
进行正则化,而不对截距参数
做正则化。首先,如果非要为参数
构造正则项,其实并不是错误的做法(虽然没有对错,但有好坏之分)。但在实际经验中,
的正则化通常对改进模型没有帮助。因为参数
这一项只代表了一条水平线,它对函数
是否平滑没有任何影响,只决定
上下移动的位置。
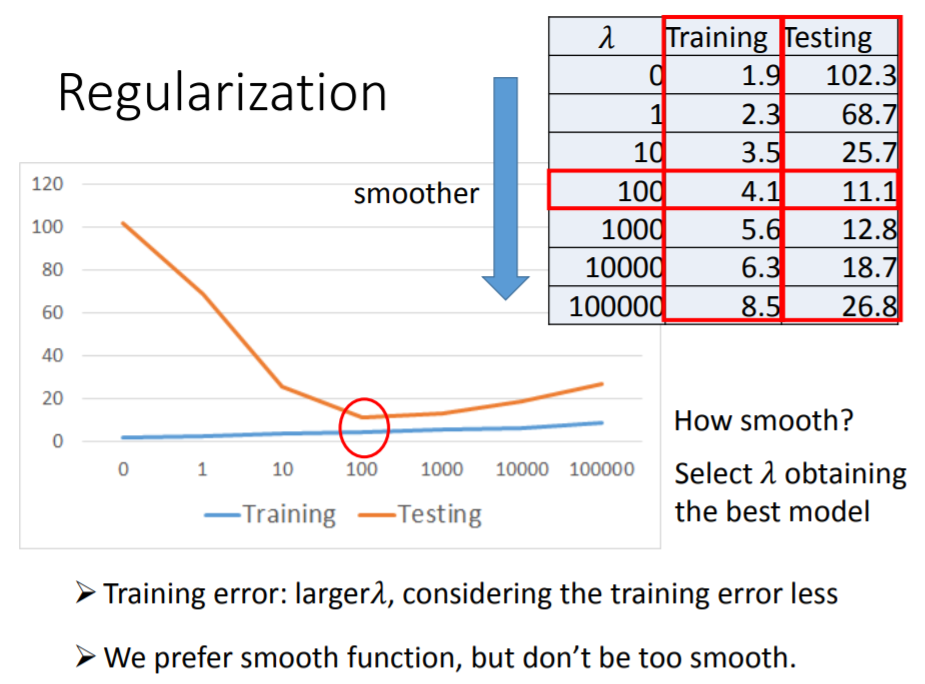
手动设置不同的正则项参数
进行拟合,随着
不断增大,得到的最佳函数
也越来越平滑。这个过程中,
在训练集的平均误差从
增大到
,这个变化是合理的:因为没有加入正则项的时候,我们的优化目标只有
,而加入正则项使我们同时要考虑减小
,使
变得平滑。并且随着
的增大,我们更倾向于得到平滑的
,这是以训练集的平均误差上升为代价的。但训练集的平均误差增大,不代表测试集的平均误差会增大。
结论
- 进化后的CP值与进化前的CP值、pokemon的种类有密切关系,但仍然可能存在其他隐藏的关联因素
- 接下来会继续介绍梯度下降法的相关理论
- 加入正则项,最后在测试集上得到的最好结果是,
,平均误差为
。假如继续收集新的数据,平均误差将会大于