ML Lecture 3-1: Gradient Descent（上）

ML Lecture 3-1: Gradient Descent

梯度下降法回顾

回顾机器学习的第三个步骤，我们需要从模型/函数集 $f_1,f_2,f_3...$ 中挑选最佳函数 $f^*$ ，这是一个求最优解的问题，需要利用损失函数。

在第二步中，我们定义的损失函数 $L$ 是关于函数的函数：把函数 $f_1,f_2,f_3...$ 逐个代入损失函数 $L$ 中，使得 $L$ 越小的 $f$ 就越好：

f^{*} = \underset{f}{a r g m i n} L (f)

$f^* = \mathop{argmin}_f L(f)$

而“把函数 $f_1,f_2,f_3...$ 逐个代入损失函数 $L$ ”这个过程太过繁琐，因此利用梯度下降法提高效率。

二参数的梯度下降过程

设参数集 $\theta = \{\theta_1,\theta_2\}$ ，包含2个参数。则梯度下降法的计算过程：

随机选取一组初始参数 $\theta^0$ ： $θ^{0} = [\begin{matrix} θ_{1}^{0} \\ θ_{2}^{0} \end{matrix}]$ $\theta^0 = \left[ \begin{matrix} \theta_1^0 \\ \theta_2^0 \\ \end{matrix} \right]$
分别计算 $L$ 对 $\theta_1$ 和 $\theta_2$ 的偏导数 $\frac{\partial L}{\partial \theta_1}$ 和 $\frac{\partial L}{\partial \theta_2}$ ，记为梯度向量 $\nabla L = \left[ \begin{matrix} \frac{\partial L}{\partial \theta_1} \\ \frac{\partial L}{\partial \theta_2} \\ \end{matrix} \right]$
计算 $\frac{\partial L}{\partial \theta_1}|_{ (\theta_1^0,\theta_2^0) }$ 和 $\frac{\partial L}{\partial \theta_2}|_{ (\theta_1^0,\theta_2^0) }$ ，将参数从 $\theta^0$ 更新至 $\theta^1$ ： $θ^{1} = [\begin{matrix} θ_{1}^{1} \\ θ_{2}^{1} \end{matrix}] = [\begin{matrix} θ_{1}^{0} \\ θ_{2}^{0} \end{matrix}] - η [\begin{matrix} \frac{\partial L}{\partial θ_{1}} |_{(θ_{1}^{0}, θ_{2}^{0})} \\ \frac{\partial L}{\partial θ_{2}} |_{(θ_{1}^{0}, θ_{2}^{0})} \end{matrix}]$ $\theta^1 = \left[ \begin{matrix} \theta_1^1 \\ \theta_2^1 \\ \end{matrix} \right] = \left[ \begin{matrix} \theta_1^0 \\ \theta_2^0 \\ \end{matrix} \right] - \eta \left[ \begin{matrix} \frac{\partial L}{\partial \theta_1}|_{ (\theta_1^0,\theta_2^0) } \\ \frac{\partial L}{\partial \theta_2}|_{ (\theta_1^0,\theta_2^0) } \\ \end{matrix} \right]$ 即 $\theta^1 = \theta^0 - \eta \nabla L (\theta^0)$
计算 $\frac{\partial L}{\partial \theta_1}|_{ (\theta_1^1,\theta_2^1) }$ 和 $\frac{\partial L}{\partial \theta_2}|_{ (\theta_1^1,\theta_2^1) }$ ，将参数从 $\theta^1$ 更新至 $\theta^2$ ： $θ^{2} = [\begin{matrix} θ_{1}^{2} \\ θ_{2}^{2} \end{matrix}] = [\begin{matrix} θ_{1}^{1} \\ θ_{2}^{1} \end{matrix}] - η [\begin{matrix} \frac{\partial L}{\partial θ_{1}} |_{(θ_{1}^{1}, θ_{2}^{1})} \\ \frac{\partial L}{\partial θ_{2}} |_{(θ_{1}^{1}, θ_{2}^{1})} \end{matrix}]$ $\theta^2 = \left[ \begin{matrix} \theta_1^2 \\ \theta_2^2 \\ \end{matrix} \right] = \left[ \begin{matrix} \theta_1^1 \\ \theta_2^1 \\ \end{matrix} \right] - \eta \left[ \begin{matrix} \frac{\partial L}{\partial \theta_1}|_{ (\theta_1^1,\theta_2^1) } \\ \frac{\partial L}{\partial \theta_2}|_{ (\theta_1^1,\theta_2^1) } \\ \end{matrix} \right]$ 即 $\theta^2 = \theta^1 - \eta \nabla L (\theta^1)$

以此类推，不断更新参数： $\theta^0 \to \theta^1 \to \theta^2...$

参数更新轨迹见如下坐标图。横、纵坐标是不同的参数变量，梯度在图中理解为一种标量场。红色线代表梯度，它是一个向量，指向损失函数的等高线的法线方向。蓝色线是参数的更新路径，注意到蓝色线与红色线恰好是方向相反的。

Tip 1：调整学习率（Tuning your learning rates）

在前面的梯度下降过程中，学习率被设为一个常数 $\eta$ 。事实上，学习率过大可能会导致无法收敛，学习率过小又会导致收敛极慢，以下图为例。

【注】：关于学习率过大、过小所带来的问题，在优化学习速率里有一个非常直观的练习。

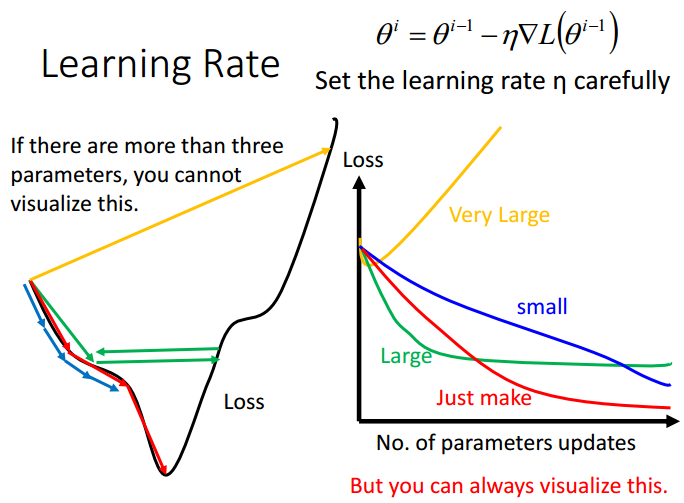
红色路径：设置适当的学习率，误差值会匀速下降，直至到达损失函数的最低点
蓝色路径：学习率太小，误差值下降十分缓慢，需要很长的时间才能到达损失函数的最低点
绿色路径：学习率较大，误差值先下降，降到一定程度后就卡住。由于更新步伐太大，只能在最低点左右震荡，始终无法抵达最低点，误差值不再发生变化
黄色路径：学习率非常大，参数直接跨过最低点，误差瞬间增大

只有当参数是一维或二维时，才能画出左边的路径图。在高维的参数空间里，无法作出路径图。但我们可以根据参数变化对损失函数值的影响，得到右边的图，观察每一次参数更新的误差变化情况，事实上做梯度下降是很有必要画出右图作参考的。接下来，考虑对学习率做一些适当的调整。

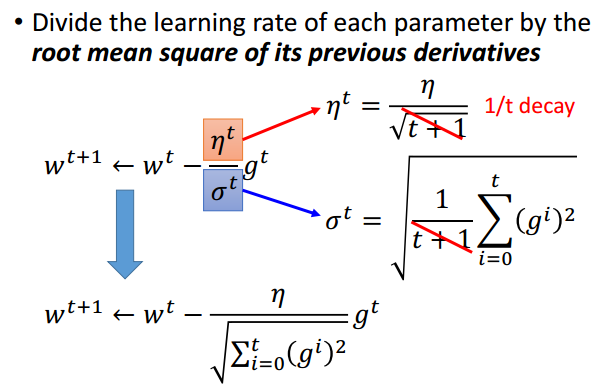
自适应学习率（Adaptive Learning Rate）之Adagrad

调整学习率的最基本、最简单的原则是：随着参数的更新，学习率应该逐渐减小。因为起始参数的位置离最低点往往比较远，所以一开始学习率应该设置大一点，加大更新步伐，加快接近目标。经过几次更新后，参数已经比较接近目标，这时就应该减小学习率，使得参数能够慢慢收敛到损失函数的最低点。

例如，把学习率设为关于迭代次数 $t$ 的函数（Time-depend Learning Rate），记为 $\eta^t$ 。随着迭代次数 $t$ 的增大， $\eta^t$ 逐渐减小：

η^{t} = \frac{η}{\sqrt{t + 1}}

$\eta^t = \frac{\eta}{\sqrt{t + 1}}$

这样做仍然是不够的，对于不同的参数应该因材施教，最好是每一个参数都赋予一个合适的学习率。即在不同的迭代过程中，对不同的参数赋予不同的学习率。这就意味着，每一个参数在每一次迭代中的学习率，都是量身定做、独一无二的。

对于上述设想，最简单有效的算法实现是Adagrad。首先考虑最简单的一维参数。假设现在要在每一轮迭代中，对一维参数 $w$ 设置不同的学习率，第 $t$ 次更新得到的参数为 $w^t$ ，损失函数 $L$ 在 $w = w^t$ 处的梯度记为 $g^t = \frac{dL}{dw}|_{w = w^t}$ ，则：

普通梯度下降（Vanilla Gradient Descent）的基本做法是，设置一个固定的学习率 $\eta$ ；或将学习率设为关于迭代次数 $t$ 的函数： $\eta^t = \frac{\eta}{\sqrt{t + 1}}$ 。参数更新过程表示为：

$(w^0 - \eta^0 g^0) \to w^1$
$(w^1 - \eta^1 g^1) \to w^2$
$...$
$(w^t - \eta^t g^t) \to w^{t + 1}$
Adagrad算法调整学习率的基本思想是：在 $\eta^t$ 的基础上，再除以过去所有导数值的均方根（Root Mean Square） $\sigma^t$ 。注意到，对于不同的参数、在不同的迭代过程中，计算出来的 $\sigma^t$ 都是不一样的，从而能够保证在多参数的情况下，每个参数都有各自的学习率。学习率表示为：
$l r = \frac{η^{t}}{σ^{t}}$ $lr = \frac{\eta^t}{\sigma^t}$ 其中， $\sigma^t = \sqrt{\frac{1}{t + 1} [(g^0)^2 + (g^1)^2 + ... + (g^t)^2]} = \sqrt{\frac{1}{t + 1} \sum_{i = 0}^t (g^i)^2}$ 。则参数更新过程可以表示为：

$(w^0 - \frac{\eta^0}{\sigma^0} g^0) = (w^0 - \frac{\eta^0}{\sqrt{(g^0)^2}} g^0) \to w^1$
$(w^1 - \frac{\eta^1}{\sigma^1} g^1) = (w^1 - \frac{\eta^1}{\sqrt{\frac{1}{2} [(g^0)^2 + (g^1)^2] }} g^1) \to w^2$
$(w^2 - \frac{\eta^2}{\sigma^2} g^2) = (w^2 - \frac{\eta^2}{\sqrt{\frac{1}{3} [(g^0)^2 + (g^1)^2 + (g^2)^2] }} g^2) \to w^3$
$...$
$(w^t - \frac{\eta^t}{\sigma^t} g^t) = (w^t - \frac{\eta^t}{\sqrt{\frac{1}{t + 1} \sum_{i = 0}^t (g^i)^2}} g^t) \to w^{t + 1}$

约掉 $\sqrt{t + 1}$ 项后，Adagrad的参数更新过程表示为：
$(w^{t} - \frac{η}{\sqrt{\sum_{i = 0}^{t} (g^{i})^{2}}} g^{t}) \to w^{t + 1}$ $(w^t - \frac{\eta}{\sqrt{\sum_{i = 0}^t (g^i)^2}} g^t) \to w^{t + 1}$ 其中， $\eta$ 为常数。

Adagrad是一种使用了自适应学习率的梯度下降优化算法，参数的更新在整体上是越来越慢的，因为加入了Time-depend因素 $t$ 。自适应包括了一系列的学习方法，Adagrad是其中最简单的一种，还有其他诸如Adadelta、Adam等。其中，Adam实操稍微比较复杂，但目前来说是比较稳定的算法。

深入理解Adagrad的更新步伐：从一维参数到多维参数

参数的更新同时取决于：学习率、梯度。

在普通梯度下降法中，学习率是一个常数 $\eta$ ，或是一个随迭代次数逐渐减小的数值 $\eta^t$ 。一开始，梯度（斜率）比较大，参数处在陡峭的地方，更新步伐大。当逐渐接近最低点，梯度慢慢减小为0。总之，学习率 $\eta^t$ 和梯度 $g^t$ 互不干涉地逐渐减小。

而在Adagrad中，学习率和梯度虽然也是逐渐减小的，但针对具体某一轮迭代的参数，学习率和梯度之间是相互牵制而非互不干涉的。比如，对于第 $t$ 次迭代，梯度为 $g^t$ ，学习率为 $\frac{\eta}{\sqrt{\sum_{i = 0}^t (g^i)^2}}$ 。显然，对于参数 $w^t$ ，它的梯度要是越大，那么学习率就越小。

为什么要这样设置学习率？或者说为什么Adagrad要以过去所有梯度的均方根 $\sqrt{\sum_{i = 0}^t (g^i)^2}$ 作为学习率的分母？如何从整体上理解Adagrad的更新步伐 $\frac{\eta g^t}{\sqrt{\sum_{i = 0}^t (g^i)^2}}$ ？

【直观上理解】定义学习率为 $\frac{\eta}{\sqrt{\sum_{i = 0}^t (g^i)^2}}$ ，是为了考察第 $i$ 次迭代梯度 $g^i$ 的反差（Surprise）程度。

如上图，第 $4$ 次迭代得到的参数记为 $w^4$ ，对应的梯度为 $g^4$ 。显然，上排的 $g^4$ 对比之前的 $g^0$ 到 $g^3$ 显著增大，而下排的 $g^4$ 对比之前的 $g^0$ 到 $g^3$ 显著减小。 为了反映从前面更新的一系列参数到下一个参数，梯度变化的反差有多大，所以除以 $\sqrt{\sum_{i = 0}^t (g^i)^2}$ 。
【从定义理解】考虑一个开口向上的二次损失函数 $y = ax^2 + bx + c$ ，其中只包含一个参数 $x$ 。易知，函数的最低点是 $(- \frac{b}{2a},\frac{4ac - b^2}{4a})$ 。作出该函数图（上），及一阶导数求绝对值后的图 $| \frac{dy}{dx} | = | 2ax + b |$ （下）：

假设现在从 $x_0$ 出发做梯度下降，那么参数更新的理想步伐（best step）应该是： $| x_0 + \frac{b}{2a} |$ （即 $x_0$ 与最小值之间的距离），意味着迭代一次就一步到位，到达最低点，找到最优参数。理想步伐整理后表示为：

$| x_{0} + \frac{b}{2 a} | = \frac{| 2 a x_{0} + b |}{2 a}$
其中，分子恰好是处的梯度，即。这个关系印证了：在损失函数上随意选取一个出发点 $x_0$ 做梯度下降，则出发点到最低点之间的距离，跟出发点处的梯度/斜率/一阶导数值是成正比的。梯度/斜率/一阶导数值越大，出发点离最低点就越远。

注意到，上面的分析只涉及一个参数 $x$ 。在多参数的情况下，“梯度/斜率/一阶导数值越大，离最低点越远”的论述就不一定成立了。

回到二参数 $w_1$ ， $w_2$ 的梯度下降。如下损失函数等高线图：横坐标为 $w_1$ ，纵坐标为 $w_2$ 。不同颜色的椭圆代表不同程度的损失值，越往内（蓝紫色部分）损失值越小。

首先，单独考察参数 $w_1$ 和 $w_2$ 对损失函数的影响：
- 对于 $w_1$ （蓝色线），在损失函数的等高线图上横向切一刀，可以看到不同等高线之间距离比较远，说明 $w_1$ 的变化对损失函数造成的影响比较平缓，对应的曲线呈宽且浅的碗状。在损失函数上取 $a$ 、 $b$ 两点，由于 $a$ 处的梯度大于 $b$ 处的梯度，所以 $a$ 点离最低点更远一些
- 对于 $w_2$ （绿色线），在损失函数的等高线图上纵向切一刀，可以看到不同等高线之间相距很近，说明 $w_2$ 的变化对损失函数造成的影响比较快，对应的曲线呈尖而深的碗状。在损失函数上取 $c$ 、 $d$ 两点，由于 $c$ 处的梯度大于 $d$ 处的梯度，所以 $c$ 点离最低点更远一些
在没有跨参数的情况下， $w_1$ 、 $w_2$ 两个参数各自都符合“梯度/斜率/一阶导数值越大，离最低点越远”的论述。但是，综合考虑 $w_1$ 和 $w_2$ 的变化：
- 想象将 $w_1$ 和 $w_2$ 的损失函数曲线放在一个坐标轴上，比较 $a$ 点和 $c$ 点，会出现与上面不符的结论：显然 $c$ 点处更陡峭，梯度更大，但 $c$ 比 $a$ 更靠近最低点
所以，在多参数的情况下，梯度/斜率/一阶导数值越大并不能说明距离最低点越远。

至此，再次明确我们的目标是，考察理想步伐：从出发点到最低点之间的距离，具有怎样的数学表达形式。

一维参数下，理想步伐为 $\frac{| 2ax_0 + b |}{2a}$ ，分子 $| 2ax_0 + b |$ 恰好是 $x= x_0$ 处的一阶导数，它告诉我们这样一个信息：梯度/斜率/一阶导数值越大，离最低点越远。分母 $2a$ 恰好是二阶导数。
尽管多维参数情况下，“梯度/斜率/一阶导数值越大，离最低点越远”的结论不一定成立，但是却可以借鉴一维参数理想步伐的数学表达式，从而得到多维参数理想步伐的数学表达形式：正比于梯度/斜率/一阶导数，反比于二阶导数。或者说，梯度/斜率/一阶导数作为分子，二阶导数作为分母。

二阶导数的本质是一阶导的变化率，从下图看出：
- $w_1$ 的二阶偏导是比较小的（横向看等高线图），因为 $w_1$ 对应的损失函数图（右侧蓝色曲线）很平缓，各点处的梯度比较小
- $w_2$ 的二阶偏导是比较大的（纵向看等高线图），因为 $w_2$ 对应的损失函数图（右侧绿色曲线）相对尖锐，各点处的梯度比较大
在二参数 $w_1$ ， $w_2$ 的情况下，光比较点 $a$ 、 $c$ 的一阶偏导值：

$\frac{\partial L}{\partial w_{1}} |_{(a, c)} 与 \frac{\partial L}{\partial w_{2}} |_{(a, c)}$
来判断它们各自离最低点有多远，是不合理的。而考虑了二阶导数后，通过比较：
$\frac{\frac{\partial L}{\partial w_{1}} |_{(a, c)}}{\frac{\partial L^{2}}{\partial w_{1}^{2}} |_{(a, c)}} 与 \frac{\frac{\partial L}{\partial w_{2}} |_{(a, c)}}{\frac{\partial L^{2}}{\partial w_{2}^{2}} |_{(a, c)}}$
虽然的一阶偏导值比较小，但除以了一个同样比较小的二阶偏导值；而的一阶偏导值比较大，但除以一个同样比较大的二阶偏导值，抵消了自身变化率的影响，这样才能真正反映当前位置与最低点之间的距离。

找到理想步伐（best step）的表达形式： $\frac{一阶导}{二阶导}$ ，这与Adagrad的更新步伐有什么关系？

注意到，Adagrad的更新步伐是：

$\frac{η g^{t}}{\sqrt{\sum_{i = 0}^{t} (g^{i})^{2}}}$
其中，分子是梯度/一阶导，而分母恰好就是二阶导的近似替代。这个形式符合理想步伐（best step）的表达形式。

那么如何理解 $\sqrt{\sum_{i = 0}^t (g^i)^2}$ 作为二阶导的近似替代？

首先，简单损失函数的二阶导其实是可以直接计算的。但在参数量大、数据多的情况下，计算一阶导都比较耗时，计算二阶导的繁琐程度可想而知。而Adagrad提供的思路是：在没有增加任何额外运算的前提下，想办法利用一阶导估计二阶导，这样我们整个运算过程就只涉及一阶导的计算。

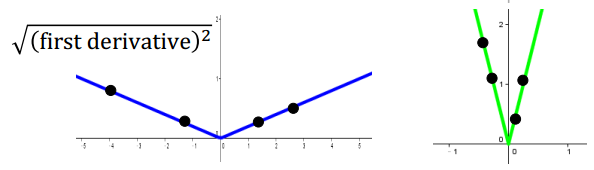
直观比较下面的损失函数图，左图平缓，每一个点的梯度小（不陡峭），梯度变化也比较慢，意味着二阶偏导较小；右图尖锐，每一个点的梯度大（陡峭），梯度变化快，意味着二阶偏导较大。

将对应的梯度/一阶导数图绘制如下。前面提到，二阶导数的本质是一阶导的变化率。在下面的图中，若随机抽取一个一阶导的样本点，是不能反映一阶导的变化情况的，即不能考察二阶导的大小。

但假如能抽取多个关于一阶导的样本点，就会发现：在左图比较平滑的损失函数里，各点处的一阶导数值普遍较小，一阶导数值之间的的变动也相对较小，从而二阶导较小；在右图比较尖锐的损失函数里，各点处的一阶导数值普遍较大，一阶导数值之间的的变动也相对较大，从而二阶导较大。
而Adagrad学习步伐的分母： $\sqrt{\sum_{i = 0}^t (g^i)^2}$ 就可以视为随着迭代次数增加，不断增加对一阶导的采样，求其均方根，以此来考察二阶导的大小，所以可以作为二阶导的近似替代。

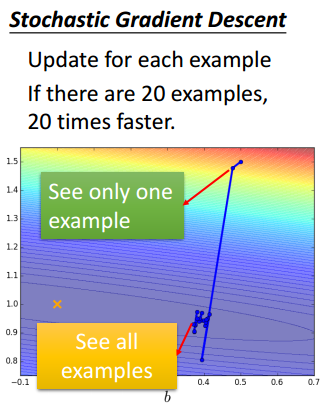
Tip 2：随机梯度下降（Stochastic Gradient Descent，SGD）：加快训练

一般地，在线性回归的梯度下降中，损失函数为：

L = \sum_{n} ({\hat{y}}^{n} - (b + \sum_{i} w_{i} x_{i}^{n}))^{2}

$L = \sum_n ( \hat{y}^n - (b + \sum_i w_i x_i^n) )^2$ 其中，

n

$n$ 是样本点的个数，

i

$i$ 是参数

w

$w$ 的个数。这里，损失函数考虑了所有训练数据的误差，对每个样本点的误差做加总后，才开始做参数的更新。 所以常规的梯度下降是拿到所有样本后，基于所有样本定义损失函数，再进行参数更新。参数更新的轨迹比较稳定，按照梯度的负方向前进。

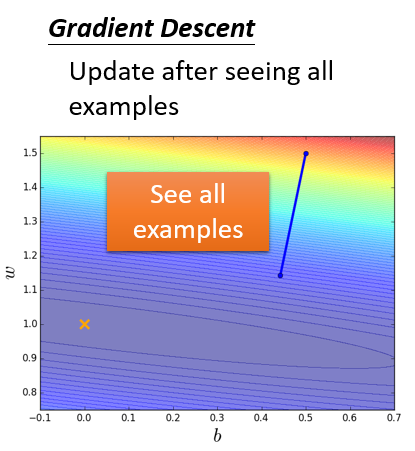
而随机梯度下降（Stochastic Gradient Descent，SGD）采取的方法是：每拿到一个样本，就针对这个样本更新一次参数，有多少个样本，参数就更新多少次。样本可以随机抽取，也可以按照顺序抽取。例如做深度学习的时候，损失函数曲线不是凸的，而是非常崎岖的，这时随机取样是比较好的。以第 $n$ 个样本为例，介绍SGD过程：

记参数集 $\theta = \{ b,w_1,w_2,..,w_i \}$ 。选择初始参数 $\theta^0 = \{ b^0,w_1^0,w_2^0,..,w_i^0 \}$
假设抽到第 $n$ 个样本 $x^n = \{ x_1^n,x_2^n,...,x_i^n \}$ ，则基于样本 $x^n$ 的损失函数（注意是单个样本的损失函数）为： $L^{n} = ({\hat{y}}^{n} - (b + \sum_{i} w_{i} x_{i}^{n}))^{2}$ $L^n = ( \hat{y}^n - (b + \sum_i w_i x_i^n) )^2$
计算损失函数对各参数的偏导： $\frac{\partial L^n}{\partial b}$ 、 $\frac{\partial L^n}{\partial w_1}$ 、 $\frac{\partial L^n}{\partial w_2}$ 、…、 $\frac{\partial L^n}{\partial w_i}$ ，记为梯度向量 $\nabla L^n$
将初始参数 $\theta^0$ 代入 $\nabla L^n$ ，得到 $\nabla L^n(\theta^0)$
做一次参数更新： $\theta^1 = \theta^0 - \eta \nabla L^n(\theta^0)$
再抽取一个样本，再更新一次参数。以此类推，假如一共有20个样本，参数就更新20次。虽然每一次更新的步伐可能比较小，且比较散乱，但相对于普通梯度下降需要一次性计算完所有样本的损失函数，随机梯度下降“见步行步”的做法收敛更快

以上两种情况相比，梯度下降处理完20个样本的损失函数后，做了一次参数更新；而随机梯度下降同样处理了20个样本，并做了20次参数更新。

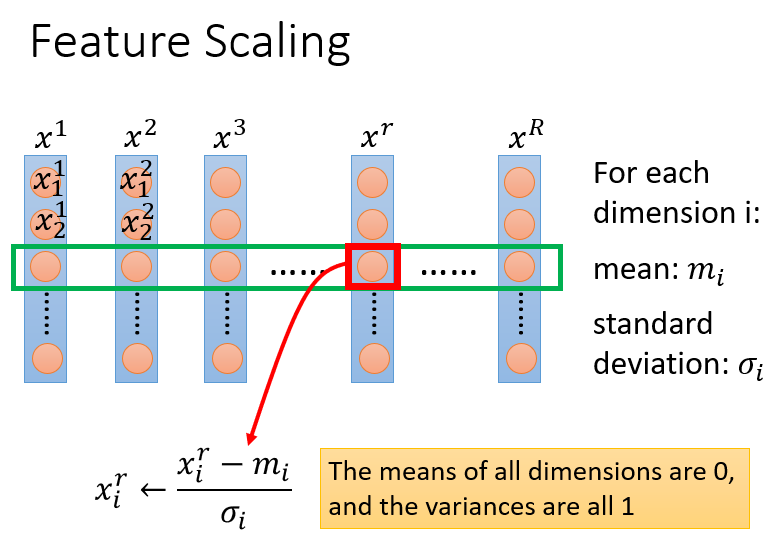
Tip 3：特征缩放（Feature Scaling）

可以理解为特征归一化。以预测pokemon进化后的CP值为例，回归任务：

y = b + w_{1} x_{1} + w_{2} x_{2}

$y = b + w_1x_1 + w_2x_2$

输入特征为 $x_1$ 、 $x_2$ ，分别代表进化前的CP值、生命值。假如 $x_1$ 和 $x_2$ 的分布范围相差十分大，则应该做缩放（归一化），使二者的分布范围一致。

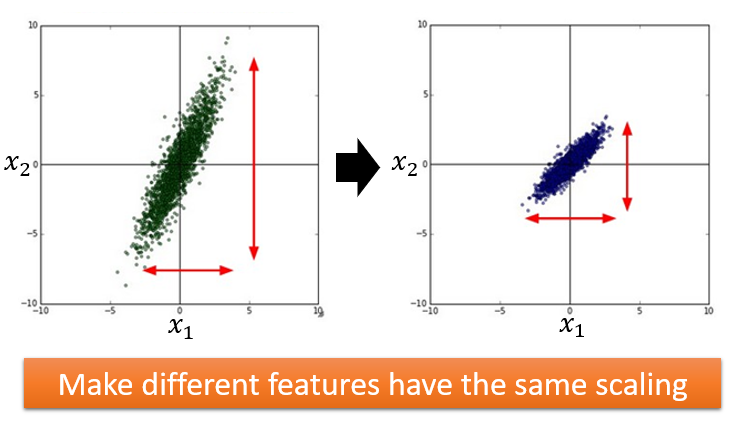
为什么要对特征做缩放？

假设 $x_1$ 的取值范围普遍比较小： $1,2,...$ ；而 $x_2$ 的取值范围普遍比较大： $100,200,...$ 。这种取值差异无疑会带来影响：当 $w_1$ 和 $w_2$ 发生同样的变化，对 $y$ 造成的影响是不同的。

显然， $w_1$ 变化时，由于 $x_1$ 取值范围不大，所以最后的变动对 $y$ 影响小，从而 $w_1$ 对 $L$ 的影响也小，因此损失函数对 $w_1$ 的偏导是比较小的，误差曲面在 $w_1$ 方向上（横向）是比较平滑的
而 $w_2$ 变化时，由于 $x_2$ 取值范围大，会给 $y$ 带来很大的变化，所以 $w_2$ 对 $L$ 的影响比较大，因此损失函数对 $w_2$ 的偏导是比较大的，误差曲面在 $w_2$ 方向上（纵向）比较窄（敏感）

没有做特征归一化的情况下，误差曲面呈长椭圆形，更新参数通常比较困难，需要使用Adagrad算法才能到达最低点，因为在不同的方向上需要不同的学习率。并且，梯度下降的方向并不是直接朝着最低点走，而是沿着等高线的法线方向前进，长椭圆形的误差曲面意味着要绕许多弯路才能走到中间。

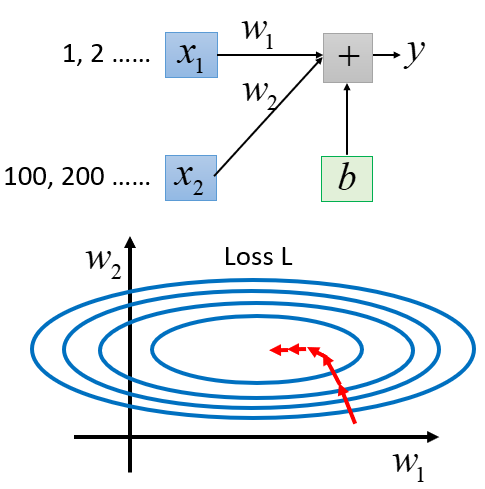
但如果能够把 $x_1$ 和 $x_2$ 的分布范围统一起来，使得 $w_1$ 、 $w_2$ 对 $L$ 的影响一致，那么误差曲面就会呈现如下图。在这种情况下，无论从哪个起点出发，梯度下降的方向就是最低点的方向，参数更新更有效率。

如何对特征做缩放？

特征缩放方法有很多种，其中最常见的是正态标准化。过程如下：

假设 $x^1,x^2,...,x^R$ 代表 $R$ 个样本，每个样本对应一组特征值。则：
样本 $x^1$ 的特征值为： $x_1^1，x_2^1，...$
样本 $x^2$ 的特征值为： $x_1^2，x_2^2，...$
样本 $x^r$ 的特征值为： $x_1^r，x_2^r，...$
求各特征的平均值 $m_i$ 与标准差 $\sigma_i$ ：
特征 $1$ 的平均值： $m_1 = \frac{1}{R} (x_1^1 + ... + x_1^R)$ ，标准差 $\sigma_1 = \sqrt{\frac{1}{R} \sum_{r = 1}^R (x_1^r - m_1)^2 }$
特征 $2$ 的平均值： $m_2 = \frac{1}{R} (x_2^1 + ... + x_2^R)$ ，标准差 $\sigma_2 = \sqrt{\frac{1}{R} \sum_{r = 1}^R (x_2^r - m_2)^2 }$
特征 $i$ 的平均值： $m_i = \frac{1}{R} (x_i^1 + ... + x_i^R)$ ，标准差 $\sigma_i = \sqrt{\frac{1}{R} \sum_{r = 1}^R (x_i^r - m_i)^2 }$
做标准化后，每个特征的取值服从标准正态分布 $N(0,1)$ ：
$x_{i}^{r} = \frac{x_{i}^{r} - m_{i}}{σ_{i}}$ $x_i^r = \frac{x_i^r - m_i}{\sigma_i}$