ML Lecture 3-1: Gradient Descent（下）

ML Lecture 3-1: Gradient Descent

梯度下降的理论基础

做梯度下降的时候，每一次迭代得到新参数，是否能保证损失函数也在不断减小？
即对于 $\theta^0 \to \theta^1 \to ...$ ，是否总是有 $L(\theta^0) > L(\theta^1) > ...$ ？

答案是否定的。在利用梯度下降更新参数的过程中，损失函数不一定总是下降，比如当学习率设置得太大，就会出现损失函数不降反增的情况。因此，了解梯度下降的工作原理，能帮助我们更快更好地寻找损失函数的最低点。

形式化推导

首先不考虑梯度下降。考察在求解最优化问题中：对于给定的整个损失函数，我们没有办法马上找到最低点。但是给定一个起始点 $\theta^0$ ，以 $\theta^0$ 为中心，划出一个直径为 $d$ 的红色圆圈，我们可以很快寻找到这个圆圈范围内的损失函数最低点 $\theta^1$ ，再将中心位置从 $\theta^0$ 移动到 $\theta^1$ 。然后以 $\theta^1$ 为中心再划分一个范围，寻找最低点，并再次更新中心点，以此类推。

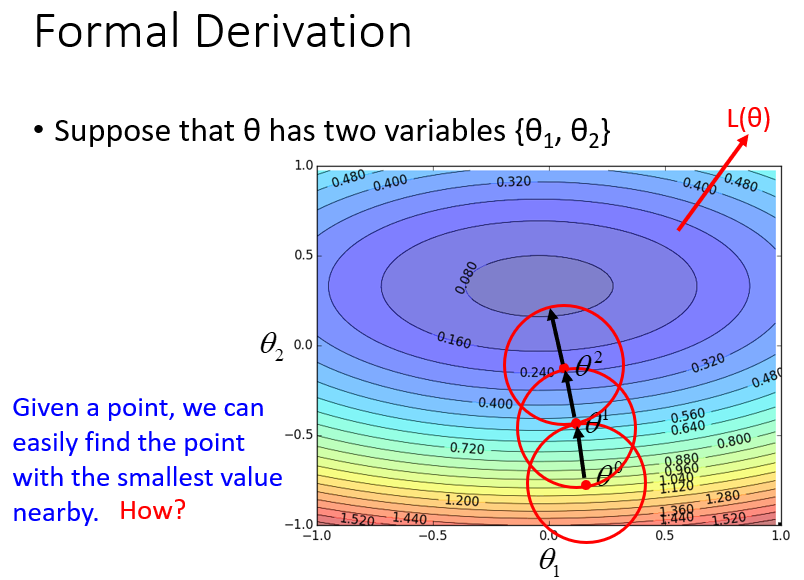
如何在红色圆圈范围内，找到使损失函数最小的参数？解决这个问题需要从泰勒级数出发。

1. 一元函数的泰勒展开

泰勒级数是指：对于任意一个函数 $h(x)$ ，如果函数在 $x = x_0$ 处无穷可微时，那么函数 $h(x)$ 可以用无限项连加式来表示：

h (x) = \sum_{k = 0}^{\infty} \frac{h^{(k)} (x_{0})}{k!} (x - x_{0})^{k} = h (x_{0}) + h^{^{'}} (x_{0}) (x - x_{0}) + \frac{h^{^{″}} (x_{0})}{2!} (x - x_{0})^{2} + . . .

$h(x) = \sum_{k = 0}^ \infty \frac{h^{(k)} (x_0)}{k!} (x - x_0)^k = h(x_0) + h^{'}(x_0)(x - x_0) + \frac{h^{''}(x_0)}{2!} (x-x_0)^2 + ...$ 其中，

h^{(k)} (x_{0})

$h^{(k)} (x_0)$ 表示函数

h

$h$ 在点

x_{0}

$x_0$ 处的

k

$k$ 阶导数。如果

x_{0} = 0

$x_0 = 0$ ，那么这个级数又称为麦克劳林级数。当

x

$x$ 非常接近

x_{0}

$x_0$ 时，

(x - x_{0}) > (x - x_{0})^{2} ≫ . . .

$(x - x_0) > (x - x_0)^2 \gg ...$ ，则

h (x)

$h(x)$ 可以表示为：

h (x) \approx h (x_{0}) + h^{^{'}} (x_{0}) (x - x_{0})

$h(x) \approx h(x_0) + h^{'}(x_0)(x - x_0)$

下图以正弦函数 $h(x) = \sin(x)$ 在点 $x_0 = \frac{\pi}{4}$ 为例，将 $\sin(x)$ 在 $\frac{\pi}{4}$ 处展开，表示成多项级数相加：

扫描二维码关注公众号，回复： 2625443 查看本文章

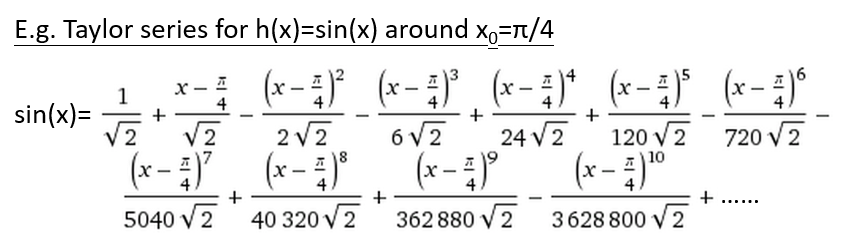
展开到 $0$ 阶导时： $\sin(x) = \frac{1}{\sqrt{2}}$ ，是一条水平线；
展开到 $1$ 阶导时： $\sin(x) = \frac{1}{\sqrt{2}} + \frac{x- \frac{\pi}{4}}{\sqrt{2}}$ ，是一条斜率为正的直线；
展开到 $2$ 阶导时： $\sin(x) = \frac{1}{\sqrt{2}} + \frac{x- \frac{\pi}{4}}{\sqrt{2}} - \frac{(x- \frac{\pi}{4})^2}{2 \sqrt{2}}$ ，是一条曲线；
…
展开到高阶导时，曲线的形状会逐渐接近真实的 $\sin (x)$ ，如图中橙色线。

观察到：只考虑 $1$ 阶导时，直线 $\frac{1}{\sqrt{2}} + \frac{x- \frac{\pi}{4}}{\sqrt{2}}$ 与 $\sin(x)$ 的真实曲线形状相差很远，但是两条线在 $x = \frac{\pi}{4}$ 附近的取值很相近。因为当 $x \to \frac{\pi}{4}$ 时， $(x-\frac{\pi}{4})^2,(x-\frac{\pi}{4})^3...$ 等的值都很小，甚至可以忽略这些项，整个式子只留下 $1$ 阶导的部分。

2. 二元函数的泰勒展开

以上情况只涉及到一个变量 $x$ ，还有多元的情况。二元函数 $h(x,y)$ 在点 $(x_0,y_0)$ 处的泰勒公式展开式为：

h (x, y) = h (x_{0}, y_{0}) + h_{x}^{^{'}} (x_{0}, y_{0}) (x - x_{0}) + h_{y}^{^{'}} (x_{0}, y_{0}) (y - y_{0}) + . . .

$h(x,y) = h(x_0,y_0) + h_x^{'} (x_0,y_0) (x - x_0) + h_y^{'} (x_0,y_0) (y - y_0) + ...$ 其中

h_{x}^{^{'}} (x_{0}, y_{0})

$h_x^{'} (x_0,y_0)$ 表示函数

h

$h$ 对

x

$x$ 的偏导数在点

(x_{0}, y_{0})

$(x_0,y_0)$ 处的值，

h_{y}^{^{'}} (x_{0}, y_{0})

$h_y^{'} (x_0,y_0)$ 表示函数

h

$h$ 对

y

$y$ 的偏导数在点

(x_{0}, y_{0})

$(x_0,y_0)$ 处的值。当

(x, y)

$(x,y)$ 非常接近

(x_{0}, y_{0})

$(x_0,y_0)$ 时，后面项的值非常小，可以忽略，于是

h (x, y)

$h(x,y)$ 可以表示为：

h (x, y) \approx h (x_{0}, y_{0}) + h_{x}^{^{'}} (x_{0}, y_{0}) (x - x_{0}) + h_{y}^{^{'}} (x_{0}, y_{0}) (y - y_{0})

$h(x,y) \approx h(x_0,y_0) + h_x^{'} (x_0,y_0) (x - x_0) + h_y^{'} (x_0,y_0) (y - y_0)$

泰勒展开与前面的形式化推导问题有什么关系？

假设损失函数是 $L(\theta) = L(\theta_1,\theta_2)$ ，在其等高线图上，初始点是 $\theta_1 = a,\theta_2 = b$ 。以 $(a,b)$ 为中心，以 $d$ 为半径，划出一个红色圆圈范围。利用泰勒展开式，将损失函数在点 $(a,b)$ 处展开：

L (θ) = L (θ_{1}, θ_{2}) \approx L (a, b) + L_{θ_{1}}^{^{'}} (a, b) (θ_{1} - a) + L_{θ_{2}}^{^{'}} (a, b) (θ_{2} - b)

$L(\theta) = L(\theta_1,\theta_2) \approx L(a,b) + L_{\theta_1}^{'}(a,b)(\theta_1 - a) + L_{\theta_2}^{'}(a,b)(\theta_2 - b)$ 其中，

L (a, b)

$L(a,b)$ 表示损失函数在点

(a, b)

$(a,b)$ 处的值，记为常数

s

$s$ ；

L_{θ_{1}}^{^{'}} (a, b)

$L_{\theta_1}^{'}(a,b)$ 表示损失函数

L

$L$ 对

θ_{1}

$\theta_1$ 的偏导在点

(a, b)

$(a,b)$ 处的值，记为常数

u

$u$ ；

L_{θ_{2}}^{^{'}} (a, b)

$L_{\theta_2}^{'}(a,b)$ 表示损失函数

L

$L$ 对

θ_{2}

$\theta_2$ 的偏导在点

(a, b)

$(a,b)$ 处的值，记为常数

v

$v$ 。记

Δ θ_{1} = θ_{1} - a

$\Delta \theta_1 = \theta_1 - a$ ，

Δ θ_{2} = θ_{2} - b

$\Delta \theta_2 = \theta_2 - b$ 。则损失函数表示为：

L (θ) = L (θ_{1}, θ_{2}) \approx s + u (θ_{1} - a) + v (θ_{2} - b) = s + u Δ θ_{1} + v Δ θ_{2}

$L(\theta) = L(\theta_1,\theta_2) \approx s + u(\theta_1 - a) +v(\theta_2 - b) = s + u \Delta \theta_1 + v \Delta \theta_2$

有了损失函数的近似表达式、不等式约束条件后，我们的具体目标转化为：在 $(\Delta \theta_1)^2 + (\Delta \theta_2)^2 \le d^2$ 的不等式约束条件下，寻找最优的 $\Delta \theta_1$ 、 $\Delta \theta_2$ ，使损失函数 $L = s + u \Delta \theta_1 + v \Delta \theta_2$ 取值最小。

由于 $s$ 是一个常数，所以只考虑不等式约束条件下 $u \Delta \theta_1 + v \Delta \theta_2$ 的最小化，这部分可以视为向量 $( \Delta \theta_1 , \Delta \theta_2 )$ 和向量 $(u,v)$ 做内积（点积）。 $u$ 、 $v$ 均是常数，应如何选择 $\Delta \theta_1$ 、 $\Delta \theta_2$ 使内积（点积）最小？

【数量积】

点积是内积的一种特殊形式，有代数、几何两种定义方式。

代数定义

两个向量 $\overrightarrow a = [a_1,a_2,...,a_n]$ 和 $\overrightarrow b = [b_1,b_2,...,b_n]$ 的点积定义为：
$\vec{a} \cdot \vec{b} = \sum_{i = 1}^{n} a_{i} b_{i} = a_{1} b_{1} + a_{2} b_{2} + . . . + a_{n} b_{n}$ $\overrightarrow a \cdot \overrightarrow b = \sum_{i = 1}^n a_i b_i = a_1 b_1 + a_2 b_2 + ... + a_n b_n$
几何定义

在欧几里得空间中，点积可以直观地定义为：
$\vec{a} \cdot \vec{b} = | \vec{a} | | \vec{b} | \cos θ$ $\overrightarrow a \cdot \overrightarrow b = | \overrightarrow a | | \overrightarrow b | \cos \theta$ 其中， $\theta$ 表示两个向量之间的角度。

从几何定义来看，模 $| \overrightarrow a |$ 、 $| \overrightarrow b |$ 始终是大于等于 $0$ 的，为了使两个向量的点积最小，应该令两向量的夹角为 $180^{\circ}$ ，即 $\cos 180^{\circ} = -1$ 。所以向量 $(\Delta \theta_1,\Delta \theta_2)$ 的方向应该与向量 $(u,v)$ 正好相反，且 $(\Delta \theta_1,\Delta \theta_2)$ 这个向量的模在红色圆圈范围内应最大限度地伸长。两个向量之间的关系应该呈现为如下数学表达形式：

[\begin{matrix} Δ θ_{1} \\ Δ θ_{2} \end{matrix}] = [\begin{matrix} θ_{1} - a \\ θ_{2} - b \end{matrix}] = - η [\begin{matrix} u \\ v \end{matrix}]

$\left[ \begin{matrix} \Delta \theta_1 \\ \Delta \theta_2 \\ \end{matrix} \right] = \left[ \begin{matrix} \theta_1 - a \\ \theta_2 - b \\ \end{matrix} \right] = - \eta \left[ \begin{matrix} u \\ v \\ \end{matrix} \right]$ 其中，

η

$\eta$ 是调整向量

[\begin{matrix} Δ θ_{1} \\ Δ θ_{2} \end{matrix}]

$\left[ \begin{matrix} \Delta \theta_1 \\ \Delta \theta_2 \\ \end{matrix} \right]$ 长度的常数。若

η

$\eta$ 能使

[\begin{matrix} Δ θ_{1} \\ Δ θ_{2} \end{matrix}]

$\left[ \begin{matrix} \Delta \theta_1 \\ \Delta \theta_2 \\ \end{matrix} \right]$ 的模刚好伸长至红色圈的边界，这个时候损失函数

L

$L$ 是最小的。

最优参数整理写为：

[\begin{matrix} θ_{1} \\ θ_{2} \end{matrix}] = [\begin{matrix} a \\ b \end{matrix}] - η [\begin{matrix} u \\ v \end{matrix}] = [\begin{matrix} a \\ b \end{matrix}] - η [\begin{matrix} L_{θ_{1}}^{^{'}} (a, b) \\ L_{θ_{2}}^{^{'}} (a, b) \end{matrix}]

$\left[ \begin{matrix} \theta_1 \\ \theta_2 \\ \end{matrix} \right] = \left[ \begin{matrix} a \\ b \\ \end{matrix} \right] - \eta \left[ \begin{matrix} u \\ v \\ \end{matrix} \right] = \left[ \begin{matrix} a \\ b \\ \end{matrix} \right] - \eta \left[ \begin{matrix} L^{'}_{\theta_1} (a,b) \\ L^{'}_{\theta_2} (a,b) \\ \end{matrix} \right]$

上式实际上就是梯度下降更新参数的过程：以 $(a,b)$ 为初始参数，求损失函数对每一个参数变量的偏导数，计算偏导数在初始点 $(a,b)$ 的偏导值，构成一个向量，即梯度。梯度乘以一个常数学习率后，与初始参数做减法，得到更新后的参数。

梯度下降的前提条件

从形式化推导的过程和结果来看，利用梯度下降方法找到最小值的前提条件是什么？或者说，满足什么条件下，梯度下降法才能奏效？

上述形式化推导过程是基于：损失函数能够近似写为 $1$ 阶导的泰勒展开。即下式能够成立：

L (θ) = s + u (θ_{1} - a) + v (θ_{2} - b)

$L(\theta) = s + u(\theta_1 - a) + v(\theta_2 - b)$ 而一个函数能在某点，近似等于

1

$1$ 阶导的泰勒展开（或者说

1

$1$ 阶泰勒展开能够作为函数的近似表达），其前提条件是：

对于一元函数 $h(x)$ ，其能够在 $x= x_0$ 处做泰勒展开，必须保证 $x$ 无限趋近于 $x_0$
对于二元函数 $L(\theta_1,\theta_2)$ ，其能够在 $(\theta_1,\theta_2) = (a,b)$ 处做泰勒展开，必须保证 $\theta_1$ 无限接近于 $a$ ， $\theta_2$ 无限接近于 $b$

因为存在约束条件 $(\theta_1 - a)^2 + (\theta_2 - b)^2 \le d^2$ ，若 $(\theta_1,\theta_2)$ 无限趋近于 $(a,b)$ ，即变量的取值 $(\theta_1,\theta_2)$ 非常接近中心点 $(a,b)$ ，则意味着红色圆圈的半径 $d$ 也必须足够小。

形式化推导最后得到的最优参数表达式即梯度下降的实现过程。这说明梯度下降能够找到最小值，是基于“ $(\theta_1,\theta_2)$ 无限趋近于 $(a,b)$ 、红圈半径 $d$ 无穷小”这个前提的。而学习率 $\eta$ 与 $d$ 是成正比的，所以理论上，学习率 $\eta$ 也要无穷小，才能保证每一次参数更新，损失函数都不断减小。

但在实操中，学习率不可能无限小，通常只要保证足够小，就可以做梯度下降。总之，学习率如果没有设置好，就会导致每次更新参数时，泰勒展开式 $L(\theta) = s + u(\theta_1 - a) + v(\theta_2 - b)$ 并不成立，梯度下降的前提都失效了，也就不能保证参数更新后损失函数是减小的。

上面的损失函数 $L$ 只考虑泰勒展开到 $1$ 阶导，事实上还可以考虑展开到 $2$ 阶导或更高阶导，此时学习率就可以设得大一点。但这里没有涉及展开到更高阶导的方法（如 $2$ 阶泰勒展开的牛顿法），是因为实践中，尤其是做深度学习，展开到高阶导的方法并不普及，因为要多计算二阶导，甚至计算Hessian矩阵及其逆矩阵，这个运算量是无法承受的，用这么复杂的运算量去换取参数更新的精度，是得不偿失的。所以做深度学习还是常用展开到 $1$ 阶导的梯度下降。

梯度下降的局限

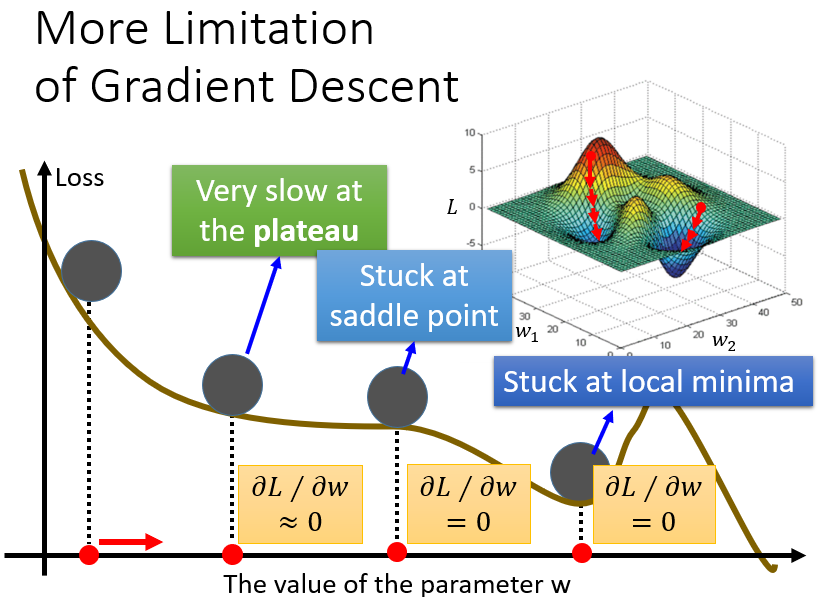
关于梯度下降的缺陷，ML Lecture 1: Regression - Case Study中提到：

随机选取初始参数，进行更新，最后可能卡在局部最小值，参数就停止更新
在整个误差曲面上，导数值为 $0$ 的点不止全局/局部最小值，也有可能是鞍点。鞍点的位置上图浅蓝色框所示，在该点处，导数值为 $0$ 却并非最小值点，参数也有可能卡在鞍点处停止更新
在实际迭代操作中，我们通常不会真的等到导数值为 $0$ ，才停止参数的更新，而是会设定一个阈值，当导数值小于此阈值时，我们就认为损失函数已经差不多接近最小值，参数也差不多接近最优，并停止迭代。但这样的做法会带来问题：绿色框对应的点，其实离全局/局部最小值、鞍点还很远，但由于处在非常平坦的地方，其计算出来的微分值特别小，每一次参数更新都只前进一点点，若此时误以为已经接近目标而停止迭代，那么求出来的参数是不理想的