ML Lecture 2: Where does the error come from?

ML Lecture 2: Where does the error come from?

• Youtube
• Bilibili
• 课件

---

随机变量的偏置（Bias）与方差(Variance)

上一节共拟合了五个线性模型，依次建立了$x_{cp}$的$1-5$次项与$y$之间的关系，其中第三个模型在测试集上的平均误差最小，第四、五个的平均误差逐渐增大。这说明，并不是越复杂的模型效果越好。同时，通过机器学习得到模型后，大多需要对模型做改进，此时就必须了解误差的来源，从而挑选适当的方法改进模型。

实际上，误差的出现来源于以下两个因素：

• 偏置（Bias）
• 方差（Variance）
  

例如，估测pokemon进化后的CP值：意味着我们要找一个函数，这个函数的输入是一只pokemon的信息，输出是这只pokemon进化后的CP值 。理论上，我们要找的这个函数存在着最佳形式，记为$\hat f$，但最佳函数$\hat f$到底是怎样的，我们无从得知。

我们只能通过收集实际的pokemon数据，利用这些训练资料做机器学习，找到我们认为最好的函数$f^*$。但是，$f^*$并不会完全等于$\hat f$，而是对$\hat f$的一个近似估计。

如果把$\hat f$视为靶心，而$f^*$作为实际打靶的落点位置。那么$\hat f$和$f^*$之间的距离，即所谓的误差，这个误差来源于两件事情：偏置或方差。首先考虑：

对于均值为$\mu$，方差为$\sigma^2$的随机变量$x$，假如我们现在对$x$一无所知，想要估计它的均值，那么我们应该：

1. 随机抽取变量$x$的$N$个样本：$x_1^{'},x_2^{'},...,x_N^{'}$
2. 计算这$N$个点的平均值$m'$： $$m' = \frac{1}{N} \sum_{n=1}^N x_n^{'}$$

样本均值$m'$可能很接近实际均值$\mu$，但不会完全等于$\mu$（除非取无限个点作为样本）。以上过程只进行了一次抽样，考虑再重复一次上述过程，作为第二次抽样：

1. 再次随机抽取变量$x$的$N$个样本：$x_1^{''},x_2^{''},...,x_N^{''}$
2. 计算这$N$个点的平均值$m''$： $$m'' = \frac{1}{N} \sum_{n=1}^N x_n^{''}$$

以此类推，重复多次抽样过程，分别获得不同的样本均值：$m^{'}$、$m^{''}$、$m^{'''}$…。随着每次抽取的样本不同，计算出来的样本均值也不同，它们平均地落在实际均值$\mu$附近，因此样本均值实际上也是一个随机变量，记为$m$，称$m$是$\mu$的无偏估计（Unbiased Estimation）：

$$E(m) = E[ \frac{1}{N} \sum_{n=1}^N x^n ] = \frac{1}{N} \sum_{n=1}^N E[ x^n ] = \mu$$

虽然每一个$m$不一定准确的等于$\mu$，但如果找很多个$m$，那它们的期望值会正好等于$\mu$。所以用$m$来估计$\mu$，我们称之为无偏的。可以将$\mu$理解为靶心，打靶时，我们的目标（即$m$的期望）是瞄准$\mu$的，但由于各种无法排除的客观因素（机械故障、手抖等），会使得落靶点$m^{'},m^{''}...$散布在本来瞄准的位置$\mu$的周围。

$m$的各个值（$m^{'},m^{''},...$）散布在$\mu$周围，其散开的程度是由$m$的方差决定的：

$$Var(m) = \frac{\sigma^2}{N}$$ $N$越大， $Var(m)$越小，则 $m^{'},m^{''},...$越集中；反之则越分散。

同理，估计随机变量$x$的方差，我们应该：

在前面计算出$m^{'},m^{''}...$的基础上，进一步计算每一次抽样的样本方差：

$$s_1^2 = \frac{1}{N} \sum_{n=1}^N (x_n^{'} - m^{'})^2$$ $$s_2^2 = \frac{1}{N} \sum_{n=1}^N (x_n^{''} - m^{''})^2$$ $$...$$

对于多次抽样获得的、不同的样本方差：$s_1^2,s_2^2,...$，它们散布在真实方差$\sigma^2$的周围。若以这些样本方差作为$\sigma^2$的估计值，会发现$s^2$普遍是小于$\sigma^2$的，也就是说$s^2$不是均匀地散落在$\sigma^2$周围，我们称$s^2$是$\sigma^2$的有偏估计（Biased Estimation）：

$$E[s^2] = \frac{N-1}{N} \sigma^2$$ 随着样本量 $N$的增大，样本方差的期望 $E[s^2]$与真实方差 $\sigma^2$之间的差距会缩小。

---

线性回归模型中的偏置与方差

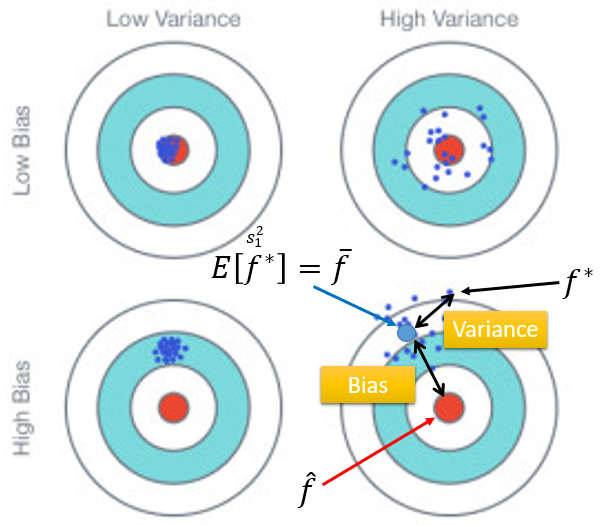
假如将回归模型中寻找最佳预测函数的过程，类比为如下打靶图。那么红色靶心是实际的估测目标$\hat f$，每一个蓝色点代表收集一次训练数据后，做机器学习获得的预测函数$f^*$。重复多次获取不同的训练集后，得到多个最佳函数$f^*$，这些$f^*$散落在$\hat f$周围。

$f^*$与$\hat f$之间的距离（误差）取决于两件事：

1. 估计量是不是无偏（眼睛有没有瞄准）：即瞄准的位置在哪里，出发点是不是对的。
   考察无偏性：计算$f^*$的期望$E(f^*)$，记为$\overline f$。以第四幅图为例，$\overline f$与$\hat f$之间的距离就是偏置（Bias），这说明瞄的时候就没有瞄准，出发点就是错的。
2. 估计量是不是有效（枪的性能好不好/手有没有抖）：确定打靶目标（出发点）的前提下，子弹发射后，落靶点与目标的偏离程度。
   考察有效性：在瞄准$\overline f$的前提下，子弹实际落在了$f^*$的位置。以第四幅图为例，$f^*$与$\overline f$之间的距离就是方差（Variance）。

最理想的状况是第一幅图：没有偏置，同时方差又很小。

第二幅图：没有偏置，但方差很大。瞄的位置是对的，$\overline f = \hat f$。但枪的性能很差或手法很不准，射偏的概率很大，散布在靶心周围。

第三幅图：偏置很大，方差很小。每次找到的$f^*$都十分接近，但都集中在错误的位置，离真正的靶心$\hat f$还有很远，因为出发点就是错的。

所以线性模型的误差取决于瞄准的位置在哪里、方差有多大。

关于方差

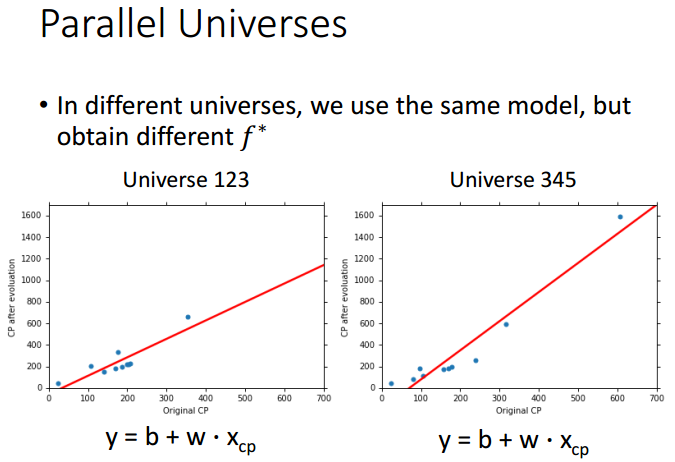
下图三人各自抓取10只pokemon，分别得到各自的训练数据的散点图。

假设以一元线性模型$y = b + w x_{cp}$为例，在两个不同的训练集上，训练出来的预测函数$f^*$也是不同的。从每个训练集上得到$f^*$就相当于对着目标射击，并得到不同落靶点的过程。

以此类推，$100$个训练集在模型$y = b + w x_{cp}$上可以得到$100$个预测函数，将其画在同一坐标图上；
$100$个训练集在模型$y = b + w_1 x_{cp} + w_2 (x_{cp})^2 + w_3 (x_{cp})^3$上可以得到$100$个预测函数，将其画在同一坐标图上；
$100$个训练集在模型$y = b + w_1 x_{cp} + w_2 (x_{cp})^2 + w_3 (x_{cp})^3 + w_4 (x_{cp})^4 + w_5 (x_{cp})^5$上可以得到$100$个预测函数，将其画在同一坐标图上。

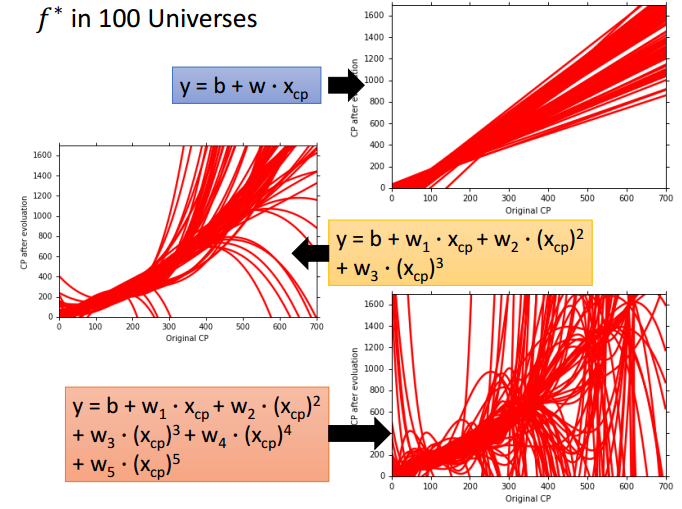
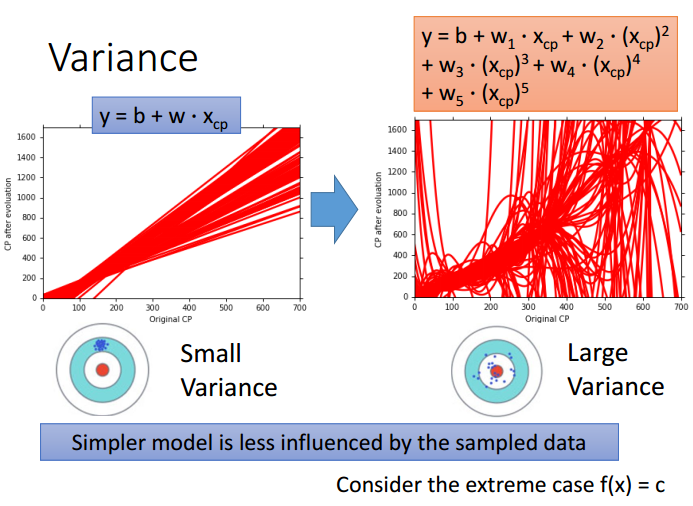
比较发现，简单模型（一次项）找到的$f^*$，方差比较小，看起来比较集中。相当于每一次射击的结果都差不多，集中在一个小范围内。而用复杂模型（五次项）找到的$f^*$，分散很开，方差较大，每一条$f^*$长得都很不像。

为什么简单模型的方差较小（分布集中），复杂模型的方差较大（分布散开）？

因为简单模型受到不同数据的影响较小。举一个极端例子：对于最简单的模型$f(x) = c$，不论输入的pokemon训练数据差异有多大，输出都是$c$。无论怎么找，$f^*$始终都是相同的（相当于没找），此时方差为$0$。随着模型复杂度的增加，方差就会逐渐增大。

关于偏置

把$100$个不同的$f^*$平均起来，找它的期望值$\overline f$。$\overline f$与真正的靶心$\hat f$之间的距离就是偏置。偏置较大意味着所有$f^*$平均起来得到的$\overline f$，到靶心还有一定的距离；偏置较小意味着尽管$f^*$可能分散得很开，但分散得再开都没关系，所有$f^*$求平均值后得到的$\overline f$，仍旧是非常接近靶心的。

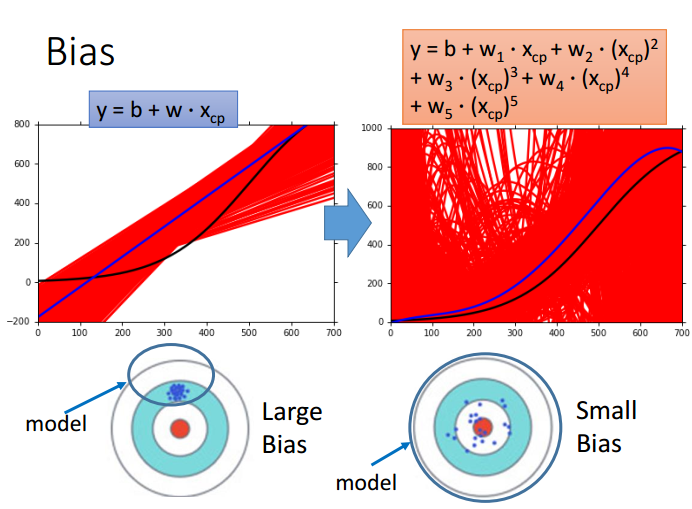
假设我们的估测目标（真实预测函数）$\hat f$如下图黑色线所示，则可以据此衡量我们所拟合的各个模型的偏置有多大。

从上往下，三幅图代表建立的模型分别为一次项、三次项、五次项。每幅图中，红色线代表$5000$个$f^*$画在同一坐标图中，蓝色线代表所有$f^*$的平均值$\overline f$，黑色线代表真实的预测函数$\hat f$。

对比三幅图，发现随着模型复杂度增加（从一次项到五次项），方差虽然逐渐增大（红色线的发散程度逐渐增大），但偏置在逐渐减小（蓝色线$\overline f$与黑色线$\hat f$逐渐吻合）。

显然，简单模型的偏置反而较大。而复杂模型，虽然每一次找出来的$f^*$都不一样，具有很大的差异性。但正是由于这种差异，使得它从平均水平上看，具有较小的偏置，更接近靶心$\hat f$。

为什么简单模型的偏置较大（平均水平离靶心远），复杂模型的偏置较小（平均水平离靶心近）？

因为一个模型就是一个函数集，里面包含了无数个可能的函数，我们要做的是从中选取最佳函数$f^*$。当我们定义了一个模型后，就已经划分出一个特定的范围，并规定只能在这个范围内寻找$f^*$。

对于简单模型（下左图），它涉及到的空间比较小，小到可能根本没有包含靶心$\hat f$。在这种情况下，无论怎么选函数、无论怎么做平均，都无法接近$\hat f$。相当于打靶的目标一开始就选错了。

而模型复杂到一定程度后（下右图），它不仅包含了简单模型在内，而且所涉及到的空间很大，很有可能包含靶心$\hat f$。在正确选择打靶目标的情况下，我们才能考虑如何在这个范围内射中靶心。

关于欠拟合与过拟合

上一节拟合了五个线性回归模型，可以很好地反映从简单模型到复杂模型，偏置、方差是如何发生变化的：
红色线代表由偏置所引起的平均误差，呈缓慢下降，说明模型越复杂，偏置因素带来的平均误差逐渐减小，相当于对目标瞄得越来越准；
绿色线代表由方差所引起的平均误差，先缓慢上升，后飙升，说明模型过度复杂会使方差急速增大，可以理解为虽然瞄得越来越准，但射靶的能力却越来越不准；
蓝色线代表由偏置和方差综合引起的平均误差，选择模型应该折衷考虑偏置和方差都比较小的情况，即第三个模型。

总之，简单/复杂模型的偏置/方差特点可以归纳如下：
1. 如果模型的偏置较大，方差较小（通常是简单模型），平均误差太大主要来自偏置影响，这种情况称为欠拟合（Underfitting）
2. 如果模型的偏置较小，方差较大（通常是复杂模型），平均误差太大主要来自方差影响，这种情况称为过拟合（Overfitting）

---

模型诊断与改进

如何判断当前模型是偏置过大，还是方差过大？两种情况下，应该分别如何做改进？

偏置较大的情况及其改进措施

如果一个模型对于少数几个样本点，都无法很好地进行拟合，说明当前模型里面可能根本没有包含目标$\hat f$（与实际正确的模型是有一段差距的），这种情况下偏置较大，属于欠拟合，可以通过如下方式重新设计模型（模型不好，收集更多的数据也没有用，要尝试使模型涵盖到目标函数$\hat f$）：

1. 重写模型的式子，加入更多的特征（光考虑$x_{cp}$可能不够，还要加入$x_{hp}$等指标）
2. 考虑更复杂的模型（从一次项到二次项、三次项等）
   

方差较大的情况及其改进措施

如果一个模型可以很好地拟合训练数据，在训练集上得到极小的误差，但在测试集上却得到很大的误差，这种情况下方差较大，属于过拟合。可以通过如下方式改进拟合效果（模型本身问题不大）：

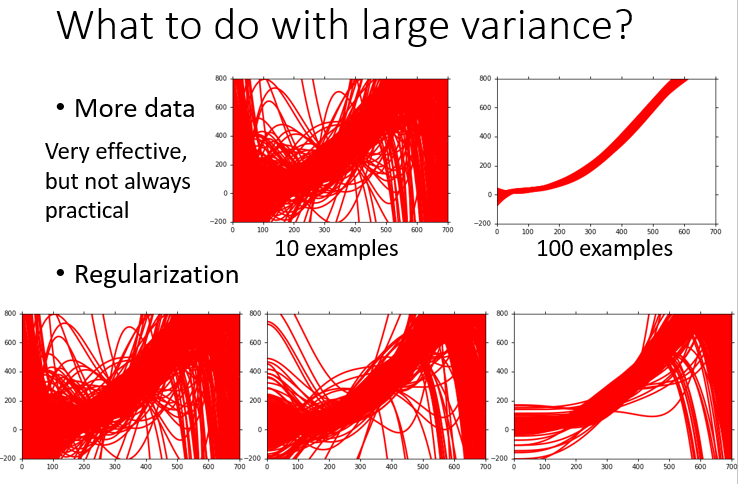
1. 收集更多数据是控制方差的有效方法（它不会影响偏置的变化），缺陷是实际中不一定能收集那么多样本：
   假设一个训练集内包含$10$只pokemon，那么$100$个训练集得到$100$个$f^*$（共$1000$只），画在同一坐标图（上左）
   假设一个训练集内包含$100$只pokemon，那么$100$个训练集得到$100$个$f^*$（共$10000$只），画在同一坐标图（上右）
   发现训练集样本量更大的情况下，$f^*$更集中，方差明显变小
2. 正则化：在损失函数$L$里加入正则项$\lambda \sum_i (w_i)^2$，构造新的损失函数$L'$。正则项的存在使$f^*$变得越来越平滑，最后挑选到的参数越来越小。常数项$\lambda$的大小决定了$f^*$的平滑程度。
   正则化的方法强迫所有曲线$f^*$变得平滑，从而降低了分散程度，减小了方差，但同时也有可能影响偏置。因为模型的可选择空间变窄了，只限定在平滑曲线的范围内，有可能远离了$\hat f$。所以做正则化的时候应调整合适的$\lambda$，使得正则项在方差和偏置之间取得平衡
   

模型选择的误区及其预防措施

面对多个模型和多个可调整的参数，我们通常是在偏置和方差之间做折衷选择，希望找到一个偏置、方差同时都很小，使得最后在测试集上平均误差很小的模型。但通常存在一些问题。

正常来说，机器学习涉及到的样本信息如下：

1. 持有的训练集（Training Set）：$x_{cp}$值、$y$值
2. 持有的测试集（Public Testing Set）：$x_{cp}$值、$y$值
3. 真正的测试集（Private Testing Set）：只有$x_{cp}$值，没有$y$值，需要真正预测$y$

利用上面的信息，机器学习的过程如下：

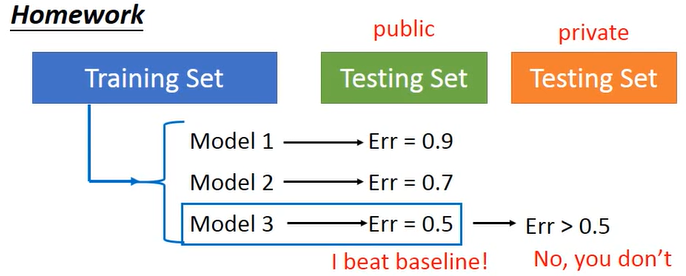
1. 准备模型，假设选择三个模型$M_1$、$M_2$、$M_3$分别拟合训练集，找到使训练集上平均误差最小的（从而是最好的）预测函数$f_1^*$、$f_2^*$、$f_3^*$
2. 将$f_1^*$、$f_2^*$、$f_3^*$对Public Set做预测，假设得到的平均误差分别为$0.9$、$0.7$、$0.5$

直觉上会认为$f_3^*$是最佳预测函数，因为它在Public Set上的平均误差最小。事实上，Public Set本身就带有一个偏置，它是我们自己持有的测试集，仍然不是真正的测试集（Private Set）。因此，通过Public Set选出来的最佳函数$f_3^*$和模型$M_3$，面对全新的Private Set，不一定能很好地预测。

如果用$f_3^*$预测Private Set的$y$值，很有可能得到平均误差大于$0.5$（但我们目前无法考证，因为手头上没有Private Set的实际$y$值信息）。

通过Public Set筛选出来的模型，在Private Set上不一定具有同样好的表现，可以通过哪些方式帮助模型选择？

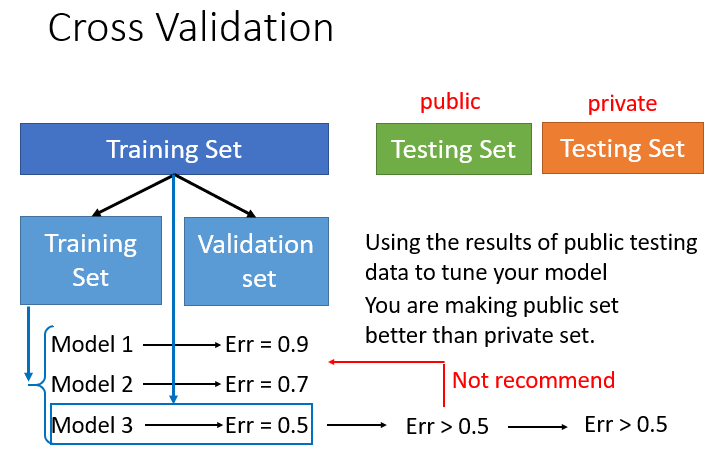
考虑将原来的训练集$T$（Training Set）分为两份：一份新的训练集$T_1$（New Training Set）用于训练模型；另一份验证集$T_2$（Validation Set）用于挑选模型：

1. 准备模型。假设准备从三个模型$M_1$、$M_2$、$M_3$中挑选，用它们分别拟合新训练集$T_1$，找到使$T_1$平均误差最小的（从而是最好的）预测函数$f_1^*$、$f_2^*$、$f_3^*$
2. 将$f_1^*$、$f_2^*$、$f_3^*$对验证集$T_2$做预测，假设得到的平均误差分别为$0.9$、$0.7$、$0.5$，那么在$T_2$上挑选出来的最佳模型是$M_3$，最优函数为$f_3^*$
3. 接下来可以直接用$f_3^*$对Public Set做预测。但是考虑到原来的训练集$T$被分成两份$T_1$、$T_2$，使得真正用来训练的数据变少，所以也可以这样做：沿用$M_3$这个模型不变，在整个训练集$T$重新寻找最优函数$(f_3^*)'$，然后用$(f_3^*)'$对Public Set做预测，这样就能保证全部的训练资料都被利用到
4. 将$(f_3^*)'$对Public Set做预测，平均误差可能大于$0.5$。但此时，$(f_3^*)'$在Public Set上的误差，是能真正反映$(f_3^*)'$在Private Set上的误差的。因为对于$(f_3^*)'$而言，Public/Private Set都是全新的，其中的信息都是没有参与到训练过程的

【注】：虽然$(f_3^*)'$在Public Set上的表现可能不佳，会出现较大的平均误差，但还是不建议返回去调整模型，以降低Public Set上的平均误差。这个做法意味着我们又根据Public Set来训练我们的模型，又被Public Set的信息带偏。最后训练出来的最佳函数，它在Public Set上的表现看似很好，平均误差看似降到很小，实质上根本无法反映模型在Private Set上的表现如何。

此外，为了防止训练集划分不合理而对训练过程造成不公平的影响，可以采用N折交叉验证（N-fold Cross Validation）。

以三折交叉验证为例：

1. 将原来的训练集$T$划分为三份$T_1$、$T_2$、$T_3$。其中两份作为新的训练集，剩下一份作为验证集，共形成三种不同的划分组合：$T_1 T_2 / T_3$、$T_1 T_3 / T_2$、$T_2 T_3 / T_1$
2. 对于每一种划分组合，分别计算三个模型$M_1$、$M_2$、$M_3$在验证集上的误差，最后计算每个模型的平均误差：$M_1$、$M_2$、$M_3$的平均误差分别为$0.3$、$0.5$、$0.4$
3. 选定平均误差最小的模型$M_1$，在整个训练集上重新寻找最优函数$(f_1^*)'$
4. 将$(f_1^*)'$对Public/Private Set做预测。原则上，尽量不要因为Public Set上的误差太大/预测表现不佳就去调整模型，这样的话，Private Set上的误差与Public Set上的误差才比较有可能是接近的