中科大-凸优化 笔记（lec40）-松弛对偶

全部笔记的汇总贴（视频也有传送门）：中科大-凸优化

例：Boolen LP问题

例：Boolen LP等价问题

$$\begin{gathered} \{\begin{array}{l}\min c^{T}x\\ s.t.Ax\le b\\ x_i(x_i-1)=0,i=1,\cdots ,n\end{array} \\ \Rightarrow L(x,\lambda ,v)=c^{T}x+{\lambda }^T(Ax-b)+\sum _{i=1}^n{v}_i{x}_i^2-\sum _{i=1}^n{v}_i{x}_i \\ =\sum _{i=1}^n{v}_i{x}_i^2+(c+A{\lambda }^T-v{)}^{T}x-{\lambda }^{T}b \\ \Rightarrow g(\lambda ,v)=\underset{x}{\inf }L(x,\lambda ,v)=\{\begin{array}{l}-{\lambda }^{T}b-\frac{1}{4}{\sum }_{i=1}^n\frac{(c_i+a_i^T\lambda -v_i{)}^2}{v_i},v\ge 0\\ -\infty ,otherwise\end{array} \\ (D)\max -{\lambda }^{T}b-\frac{1}{4}\sum _{i=1}^n\frac{(c_i+a_i^T\lambda -v_i{)}^2}{v_i} \\ s.t.\lambda \ge 0,v\ge 0 \\ \underset{\lambda ,v}{\max }f(\lambda ,v)=\underset{\lambda }{\max }\underset{v}{\max }f(\lambda ,v) \end{gathered}$$

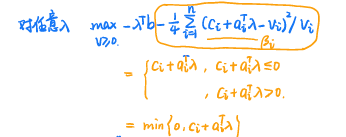
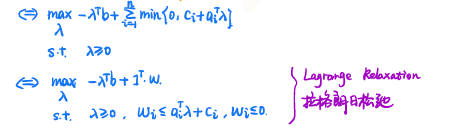
例：带等式约束的可微凸优化问题

下一章传送门：中科大-凸优化 笔记（lec41）-可微凸优化问题的罚函数形式