全部笔记的汇总贴(视频也有传送门):中科大-凸优化

一、多面体(Polyhedron)
P = { x ∣ a j T x ≤ b j j = 1 , ⋯ , m , c j T x = d j j = 1 , ⋯ , r } P=\{x|a_j^Tx\le b_j\;j=1,\cdots,m,c_j^Tx=d_j\;j=1,\cdots,r\} P={ x∣ajTx≤bjj=1,⋯,m,cjTx=djj=1,⋯,r}
② √
- 有界多面体
二、单纯形(Simplex)
一种特殊的多面体。
R n \R^n Rn空间中选择 v 0 , ⋯ , v k v_0,\cdots,v_k v0,⋯,vk共 k + 1 k+1 k+1个点, v 1 − v 0 , ⋯ , v k − v 0 v_1-v_0,\cdots,v_k-v_0 v1−v0,⋯,vk−v0线性无关,则与上述点相关的单纯形为 C = c o n v { v 0 , ⋯ , v k } = { θ 0 v 0 + ⋯ + θ k v k ∣ θ ≥ 0 , 1 T θ = 1 } C=conv\{v_0,\cdots,v_k\}=\{\theta_0v_0+\cdots+\theta_kv_k|\theta\ge0,1^T\theta=1\} C=conv{
v0,⋯,vk}={
θ0v0+⋯+θkvk∣θ≥0,1Tθ=1}
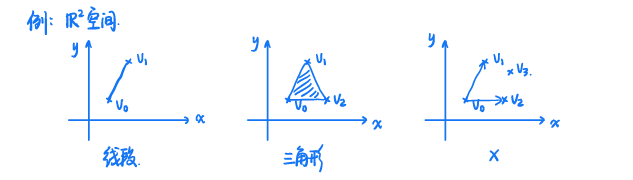
证明simplex是polyhedron的一种
x ∈ C ∈ R n , C 为 s i m p l e x ⇔ x = θ 0 v 0 + ⋯ + θ k v k , 1 T θ = 1 , θ ≥ 1 v 1 − v 0 , ⋯ , v k − v 0 线 性 无 关 定 义 [ θ 1 , ⋯ , θ k ] T = y , y ≥ 0 , 1 T y ≤ 1 [ v 1 − v 0 , ⋯ , v k − v 0 ] = B ∈ R n ∗ k x ∈ C ⇔ x = θ 0 v 0 + ⋯ + θ k v k = v 0 + θ 1 ( v 1 − v 0 ) + ⋯ + θ k ( v k − v 0 ) = v 0 + B y x\in C\in \R^n,C为simplex \Leftrightarrow x=\theta_0v_0+\cdots+\theta_kv_k,1^T\theta=1,\theta\ge1\\v_1-v_0,\cdots,v_k-v_0线性无关\\定义[\theta_1,\cdots,\theta_k]^T=y,y\ge0,1^Ty\le1\\ [v_1-v_0,\cdots,v_k-v_0]=B\in\R^{n*k}\\\;\\x\in C\\\Leftrightarrow x=\theta_0v_0+\cdots+\theta_kv_k\\=v_0+\theta_1(v_1-v_0)+\cdots+\theta_k(v_k-v_0)\\=v_0+By x∈C∈Rn,C为simplex⇔x=θ0v0+⋯+θkvk,1Tθ=1,θ≥1v1−v0,⋯,vk−v0线性无关定义[θ1,⋯,θk]T=y,y≥0,1Ty≤1[v1−v0,⋯,vk−v0]=B∈Rn∗kx∈C⇔x=θ0v0+⋯+θkvk=v0+θ1(v1−v0)+⋯+θk(vk−v0)=v0+By
r a n k ( B ) = k ( k ≤ n ) 非 奇 异 值 矩 阵 A = ( A 1 A 2 ) ∈ R n ∗ n A B = ( A 1 A 2 ) B = ( 1 k 0 ( n − k ) ∗ k ) rank(B)=k(k\le n)\;\;非奇异值矩阵 A=\begin{pmatrix} A_1\\A_2\end{pmatrix}\in\R^{n*n}\\AB=\begin{pmatrix} A_1\\A_2\end{pmatrix}B=\begin{pmatrix} 1_k\\0_{(n-k)*k}\end{pmatrix} rank(B)=k(k≤n)非奇异值矩阵A=(A1A2)∈Rn∗nAB=(A1A2)B=(1k0(n−k)∗k)
x = v 0 + B y ⇔ A x = A v 0 + A B y ⇔ ( A 1 A 2 ) x = ( A 1 A 2 ) v 0 + ( A 1 B A 2 B ) y ⇔ A 1 x = A 1 v 0 + y ( ← 变 量 ) A 2 x = A 2 v 0 ⇔ A 1 x ≥ A 1 v 0 1 T A 1 x ≤ 1 + 1 T A v 0 A 2 x = A 2 v 0 x=v_0+By\\\Leftrightarrow Ax=Av_0+ABy\\\Leftrightarrow \begin{pmatrix} A_1\\A_2\end{pmatrix}x=\begin{pmatrix} A_1\\A_2\end{pmatrix}v_0+\begin{pmatrix} A_1B\\A_2B\end{pmatrix}y\\\;\\\Leftrightarrow \begin{matrix} A_1x=A_1v_0+y(\leftarrow变量)\\A_2x=A_2v_0\end{matrix}\\\;\\\Leftrightarrow \begin{matrix} A_1x\ge A_1v_0\\1^TA_1x\le 1+1^TAv_0\\A_2x=A_2v_0\end{matrix} x=v0+By⇔Ax=Av0+ABy⇔(A1A2)x=(A1A2)v0+(A1BA2B)y⇔A1x=A1v0+y(←变量)A2x=A2v0⇔A1x≥A1v01TA1x≤1+1TAv0A2x=A2v0
三、一些矩阵集合也是凸集,甚至是凸锥
对称矩阵集合 S n = { x ∈ R n ∗ n ∣ x = x T } S^n=\{x\in\R^{n*n}|x=x^T\} Sn={
x∈Rn∗n∣x=xT},是凸锥。
对称半正定矩阵集合 S + n = { x ∈ R n ∗ n ∣ x = x T , x ⪰ 0 } S^n_+=\{x\in\R^{n*n}|x=x^T,x\succeq0\} S+n={
x∈Rn∗n∣x=xT,x⪰0},是凸集,也是凸锥。
对称正定矩阵集合 S + + n = { x ∈ R n ∗ n ∣ x = x T , x ≻ 0 } S^n_{++}=\{x\in\R^{n*n}|x=x^T,x\succ0\} S++n={
x∈Rn∗n∣x=xT,x≻0},不是凸锥。
证明: S + n S_+^n S+n是convex Cone
∀ θ 1 , θ 2 ≥ 0 , ∀ A , B ∈ S + n , 证 明 θ 1 A + θ 2 B ∈ S + n ∀ x ∈ R n , x T A x ≥ 0 , x T B x ≥ 0 x T ( θ 1 A + θ 2 B ) x = θ 1 x T A x + θ 2 x T A x ≥ 0 \forall \theta_1,\theta_2\ge0,\forall A,B\in S_+^n,证明\theta_1A+\theta_2B\in S_+^n\\\forall x\in\R^n,x^TAx\ge0,x^TBx\ge0\\x^T(\theta_1A+\theta_2B)x=\theta_1x^TAx+\theta_2x^TAx\ge0 ∀θ1,θ2≥0,∀A,B∈S+n,证明θ1A+θ2B∈S+n∀x∈Rn,xTAx≥0,xTBx≥0xT(θ1A+θ2B)x=θ1xTAx+θ2xTAx≥0
同理, S n S^n Sn是凸锥
S + + n S^n_{++} S++n不是凸锥。
例: n = 1 n=1 n=1,则 S + n = R + S_+^n=\R_+ S+n=R+, S + + n = R + + S_{++}^n=\R_{++} S++n=R++, S n = R S^n=\R Sn=R,正定矩阵集合不包含零矩阵,所以不是凸锥。
S + n n = 2 S + n = { ( x t y z ) ∣ x ≥ 0 , z ≥ 0 , x z ≥ y 2 } S_+^n\;\;n=2 \;\; S_+^n=\{\begin{pmatrix} x & t \\ y & z \end{pmatrix}\Big|x\ge0,z\ge0,xz\ge y^2\} S+nn=2S+n={ (xytz)∣∣∣x≥0,z≥0,xz≥y2}
下一章传送门:中科大-凸优化 笔记(lec7)-保凸变换(上)