全部笔记的汇总贴(视频也有传送门):中科大-凸优化
一、椭球是球的仿射映射
ε = { x ∣ ( x − x c ) T P − 1 ( x − x c ) } P ∈ S + + n { u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } P 1 2 P 1 2 = P \varepsilon=\{x|(x-x_c)^TP^{-1}(x-x_c)\}\;\;P\in S_{++}^n\\\{u|\;||u||_2\le1\}\;\;\;P^{\frac12}P^{\frac12}=P ε={
x∣(x−xc)TP−1(x−xc)}P∈S++n{
u∣∣∣u∣∣2≤1}P21P21=P
f ( u ) = P 1 2 u + x c { f ( u ) ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } = { P 1 2 u + x c ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } f(u)=P^{\frac12}u+x_c\\\{f(u)|\;||u||_2\le1\}=\{P^{\frac12}u+x_c|\;||u||_2\le1\} f(u)=P21u+xc{
f(u)∣∣∣u∣∣2≤1}={
P21u+xc∣∣∣u∣∣2≤1}
我们令 x = Δ P 1 2 u + x c u = P − 1 2 ( x − x c ) x\overset{\Delta}{=}P^{\frac12}u+x_c\;\;\;u=P^{-\frac12}(x-x_c) x=ΔP21u+xcu=P−21(x−xc)
所以, { f ( u ) ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } = { x ∣ ∣ ∣ P − 1 2 ( x − x c ) ∣ ∣ 2 ≤ 1 } = { x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } \{f(u)|\;||u||_2\le1\}=\{x|\;||P^{-\frac12}(x-x_c)||_2\le1\}\\=\{x|(x-x_c)^TP^{-1}(x-x_c)\le1\} {
f(u)∣∣∣u∣∣2≤1}={
x∣∣∣P−21(x−xc)∣∣2≤1}={
x∣(x−xc)TP−1(x−xc)≤1}
二、透视函数(Perspective Function)
P : R n + 1 → R n d o m P = R n ∗ R + + P:\R^{n+1}\rightarrow\R^n\;\;\;\;\;dom \;P=R^n*R_{++} P:Rn+1→RndomP=Rn∗R++
P ( z , t ) = z t z ∈ R n , t ∈ R + + P(z,t)=\frac zt\;\;\;\;z\in \R^n,t\in\R_{++} P(z,t)=tzz∈Rn,t∈R++
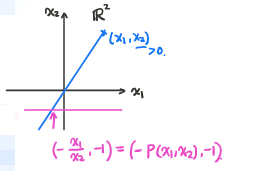
考虑 R n + 1 \R^{n+1} Rn+1内线段, x = ( x ~ ∈ R n , x n + 1 ∈ R + + ) y = ( y ~ ∈ R n , y n + 1 ∈ R + + ) x=(\underset{\in\R^n}{\widetilde{x}},\underset{\in\R_{++}}{x_{n+1}})\;\;\;y=(\underset{\in\R^n}{\widetilde{y}},\underset{\in\R_{++}}{y_{n+1}}) x=(∈Rnx
,∈R++xn+1)y=(∈Rny
,∈R++yn+1)
θ ≥ 0 \theta\ge0 θ≥0,线段为 θ x + ( 1 − θ ) y \theta x+(1-\theta)y θx+(1−θ)y
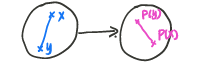
证明 线段 → P \overset{P}{\rightarrow} →P线段 x → P P ( x ) \;\;\;\;\;\;\;\;x\overset{P}{\rightarrow}P(x) x→PP(x) y → P P ( y ) \;\;\;\;\;\;\;\;y\overset{P}{\rightarrow}P(y) y→PP(y)
θ x + ( 1 − θ ) y → P P ( θ x + ( 1 − θ ) y ) \theta x+(1-\theta)y\overset{P}{\rightarrow}P(\theta x+(1-\theta)y) θx+(1−θ)y→PP(θx+(1−θ)y)
P ( θ x + ( 1 − θ ) y ) = θ x ~ + ( 1 − θ ) y ~ θ x n + 1 + ( 1 − θ ) y n + 1 = θ x n + 1 θ x n + 1 + ( 1 − θ ) y n + 1 μ ∈ [ 0 , 1 ] ⋅ x ~ x n + 1 P ( x ) + ( 1 − θ ) y n + 1 θ x n + 1 + ( 1 − θ ) y n + 1 1 − μ ⋅ y ~ y n + 1 P ( y ) = μ P ( x ) + ( 1 − μ ) P ( y ) P(\theta x+(1-\theta)y)=\frac{\theta \widetilde{x}+(1-\theta)\widetilde{y}}{\theta x_{n+1}+(1-\theta)y_{n+1}}\\=\underset{\color{blue}\mu\in[0,1]}{\frac{\theta x_{n+1}}{\theta x_{n+1}+(1-\theta)y_{n+1}}}\cdot\underset{\color{blue}P(x)}{\frac{\widetilde{x}}{x_{n+1}}}+\underset{\color{blue}1-\mu}{\frac{(1-\theta)y_{n+1}}{\theta x_{n+1}+(1-\theta)y_{n+1}}}\cdot\underset{\color{blue}P(y)}{\frac{\widetilde{y}}{y_{n+1}}}\\=\mu P(x)+(1-\mu)P(y) P(θx+(1−θ)y)=θxn+1+(1−θ)yn+1θx
+(1−θ)y
=μ∈[0,1]θxn+1+(1−θ)yn+1θxn+1⋅P(x)xn+1x
+1−μθxn+1+(1−θ)yn+1(1−θ)yn+1⋅P(y)yn+1y
=μP(x)+(1−μ)P(y)
θ → μ \theta\rightarrow\mu θ→μ是透视映射
任意凸集的反透视映射仍是凸集
P − 1 ( C ) = { ( x , t ) ∈ R n + 1 ∣ x t ∈ C , t > 0 } P^{-1}(C)=\{(x,t)\in\R^{n+1}|\frac xt\in C,t>0\} P−1(C)={
(x,t)∈Rn+1∣tx∈C,t>0}
考虑 ( x , t ) ∈ P − 1 ( C ) ( y , S ) ∈ P − 1 ( C ) , 0 ≤ θ ≤ 1 (x,t)\in P^{-1}(C)\;\;(y,S)\in P^{-1}(C),0\le\theta\le1 (x,t)∈P−1(C)(y,S)∈P−1(C),0≤θ≤1
θ x + ( 1 − θ ) y θ t + ( 1 − θ ) S = θ t θ t + ( 1 − θ ) S μ ⋅ x t ∈ C + ( 1 − θ ) S θ t + ( 1 − θ ) S 1 − μ ⋅ y S ∈ C ∈ C \frac{\theta x+(1-\theta)y}{\theta t+(1-\theta)S}=\underset{\color{blue}\mu}{\frac{\theta t}{\theta t+(1-\theta)S}}\cdot\underset{\color{blue}\in C}{\frac xt}+\underset{\color{blue}1-\mu}{\frac{(1-\theta)S}{\theta t+(1-\theta)S}}\cdot\underset{\color{blue}\in C}{\frac yS}{\color{red}\in C} θt+(1−θ)Sθx+(1−θ)y=μθt+(1−θ)Sθt⋅∈Ctx+1−μθt+(1−θ)S(1−θ)S⋅∈CSy∈C
三、线性分数函数
线性分数函数 f f f(由点 x x x先做个仿射变换,再做个透视得到)
g : R n → R m + 1 g:\R^n\rightarrow\R^{m+1} g:Rn→Rm+1为仿射映射, g ( x ) = ( A C T ) x + ( b d ) A ∈ R m ∗ n , C ∈ R n , b ∈ R m , d ∈ R g(x)=\begin{pmatrix} A\\C^T\end{pmatrix}x+\begin{pmatrix} b\\d\end{pmatrix}\;\;\;\;\;A\in\R^{m*n},C\in\R^n,b\in\R^m,d\in\R g(x)=(ACT)x+(bd)A∈Rm∗n,C∈Rn,b∈Rm,d∈R
P : R m + 1 → R m P:\R^{m+1}\rightarrow\R^m P:Rm+1→Rm为透视变换
f : R n → R m = Δ P ⋅ g f:\R^n\rightarrow\R^m\overset{\Delta}{=}P\cdot g f:Rn→Rm=ΔP⋅g(复合函数)线性分数函数 P ( g ( C ) ) P(g(C)) P(g(C))
f ( x ) = A x + b C T x + d , d o m f = { x ∣ C T x + d > 0 } f(x)=\frac{Ax+b}{C^Tx+d},\;\;dom\;f=\{x|C^Tx+d>0\} f(x)=CTx+dAx+b,domf={ x∣CTx+d>0}
- 线性分数变换是一个保凸变换,但是它其实是一个非线性变换,所以很特殊的。
两个随机变量的联合概率 ⟶ 映 射 \overset{映射}{\longrightarrow} ⟶映射条件概率(保凸映射)
u = { 1 , ⋯ , n } v = { 1 , ⋯ , m } u=\{1,\cdots,n\}\;\;v=\{1,\cdots,m\} u={ 1,⋯,n}v={ 1,⋯,m}
联合概率: P i j = P ( u = i , v = j ) P_{ij}=P(u=i,v=j) Pij=P(u=i,v=j)
条件概率: f i j = P ( u = i ∣ v = j ) f_{ij}=P(u=i|v=j) fij=P(u=i∣v=j)
由条件概率的定义可知: f i j = P i j ∑ k = 1 n P k j f_{ij}=\frac{P_{ij}}{\sum_{k=1}^nP_{kj}} fij=∑k=1nPkjPij
这是一个线性分式映射,因为可以写成 f i j = ( 0 , ⋯ , 1 , ⋯ , 0 ) ( P 1 j , ⋯ , P n j ) T 1 T ( P 1 j , ⋯ , P n j ) T = A x + 0 C T x + 0 f_{ij}=\frac{(0,\cdots,1,\cdots,0)(P_{1j},\cdots,P_{nj})^T}{1^T(P_{1j},\cdots,P_{nj})^T}=\frac{Ax+0}{C^Tx+0} fij=1T(P1j,⋯,Pnj)T(0,⋯,1,⋯,0)(P1j,⋯,Pnj)T=CTx+0Ax+0
成立的前提是证明 { P i j } \{P_{ij}\} { Pij}是一个凸集。