中科大-凸优化 笔记（lec20）-可微拟凸函数的一阶/二阶条件

全部笔记的汇总贴（视频也有传送门）：中科大-凸优化

一、可微拟凸函数的一阶条件

凸$\iff domf$为凸，$f(y)\ge f(x)+\nabla f^T(x)(y-x),\forall x,y\in domf$

拟凸$\iff domf$为凸，$f(y)\le f(x)\Rightarrow \nabla f^T(x)(y-x)\le 0,\forall x,y\in domf$

• 证明（$\Rightarrow$）

x , y ∈ d o m    f , 0 ≤ θ ≤ 1 max ⁡ { f ( x ) , f ( y ) } ≥ f ( θ x + ( 1 − θ ) y ) 设 f ( y ) ≤ f ( x ) ， 则 f ( x ) ≥ f ( θ x + ( 1 − θ ) y ) f ( θ x + ( 1 − θ ) y ) − f ( x ) ≤ 0 ⇔ f ( θ x + ( 1 − θ ) y ) − f ( θ x + ( 1 − θ ) y ) ≤ 0 ⇔ f ( θ x + ( 1 − θ ) y ) − f ( θ x + ( 1 − θ ) x ) ( 1 − θ ) ( y − x ) ( 1 − θ ) ( y − x ) ≤ 0 ( 令 θ → 1 − ) ⇔ f ′ ( x ) ( y − x ) ≤ 0 x,y\in dom\;f,0\le\theta\le1\\\max\{f(x),f(y)\}\ge f(\theta x+(1-\theta)y)\\设f(y)\le f(x)，则f(x)\ge f(\theta x+(1-\theta)y)\\f(\theta x+(1-\theta)y)-f(x)\le0\\\Leftrightarrow f(\theta x+(1-\theta)y)-f(\theta x+(1-\theta)y)\le0\\\Leftrightarrow\frac{f(\theta x+(1-\theta)y)-f(\theta x+(1-\theta)x)}{(1-\theta)(y-x)}(1-\theta)(y-x)\le0\\(令\theta\rightarrow1_-)\Leftrightarrow f'(x)(y-x)\le0 x,y∈domf,0≤θ≤1max{ f(x),f(y)}≥f(θx+(1−θ)y)设f(y)≤f(x)，则f(x)≥f(θx+(1−θ)y)f(θx+(1−θ)y)−f(x)≤0⇔f(θx+(1−θ)y)−f(θx+(1−θ)y)≤0⇔(1−θ)(y−x)f(θx+(1−θ)y)−f(θx+(1−θ)x)​(1−θ)(y−x)≤0(令θ→1−​)⇔f′(x)(y−x)≤0

• 证明（$\Leftarrow$）

∀ x , y ∈ d o m    f 均 有 f ( y ) ≤ f ( x ) ， 则 ∇ f T ( x ) ( y − x ) ≤ 0 max ⁡ { f ( y ) , f ( x ) } − f ( θ x + ( 1 − θ ) y ) = f ( x ) − f ( θ x + ( 1 − θ ) y ) = f ( θ x + ( 1 − θ ) x ) − f ( θ x + ( 1 − θ ) y ) ( 1 − θ ) ( y − x ) ( 1 − θ ) ( y − x ) ( 令 θ → 1 − ) = f ′ ( x ) ( x − y ) ≥ 0 \forall x,y\in dom\;f均有f(y)\le f(x)，则\nabla f^T(x)(y-x)\le0\\\max\{ f(y),f(x)\}-f(\theta x+(1-\theta)y)=f(x)-f(\theta x+(1-\theta)y)\\=\frac{f(\theta x+(1-\theta)x)-f(\theta x+(1-\theta)y)}{(1-\theta)(y-x)}(1-\theta)(y-x)\\(令\theta\rightarrow1_-)= f'(x)(x-y)\ge0 ∀x,y∈domf均有f(y)≤f(x)，则∇fT(x)(y−x)≤0max{ f(y),f(x)}−f(θx+(1−θ)y)=f(x)−f(θx+(1−θ)y)=(1−θ)(y−x)f(θx+(1−θ)x)−f(θx+(1−θ)y)​(1−θ)(y−x)(令θ→1−​)=f′(x)(x−y)≥0

凸$\iff$若$\nabla f^T(x)=0$，则$\forall y,f(y)\ge f(x)$（最优值点）

拟凸$\iff$若$\nabla f^T(x)=0$，则$\forall y,f(y)\le f(x)\Rightarrow \theta \le 0$（没有意义）

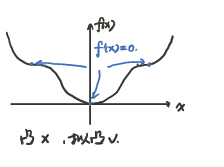
二、可微拟凸函数的二阶条件

凸：$domf$为凸，且$\nabla f^T(x)⪰0,\forall x\in domf$

拟凸：$domf$为拟凸，且$y^T\nabla f(x)\ge 0\Rightarrow y^T{\nabla }^{2}f(x)y\ge 0$（都是常量，关键点：黑塞矩阵是半正定的）

$n=1$时，$y{f}^{\prime }(x)\ge 0\Rightarrow y^2{f}^{\prime \prime }(x)\ge 0$
$$\{\begin{array}{l}y=00\ge 0\\ \\ f^{\prime }(x)=0,y\ne 0\Rightarrow f^{\prime \prime }(x)\ge 0\end{array}$$

$$\begin{gathered} logconcave:f:{\mathbb{R}}^n\to \mathbb{R}为logconcave，若f(x)>0,\forall x\in domf且logf为凹函数 \\ logconvex:f:{\mathbb{R}}^n\to \mathbb{R}为logconvex，若f(x)>0,\forall x\in domf且logf为凸函数 \end{gathered}$$

若$f$为$logconvex$，则$f$为$convex$$$f=e^{\log f}为凸，令h(x)=e^x,g(x)=\log f，用复合函数的凸性判断$$

若$f$为$concave,f>0$，则$\log f$为$logconcave$$$f=\log f为凹$$