中科大-凸优化 笔记（lec14）-保凸运算

全部笔记的汇总贴（视频也有传送门）：中科大-凸优化

一、保持函数凸性

非负加权和：$f_1,\cdots ,f_n$为凸，则$f={\sum }_{i=1}^m{w}_i{f}_i$为凸，若$w_i\ge 0,\forall i$
1.定义域是凸集 2.不等式

若$f(x,y)$，对任意$y\in A,f(x,y)$均为凸$$(x,y)jointlyconvex$$

设$w(y)\ge 0,\forall y\in A,g(x)={\int }_{y\in A}w(y)f(x,y)dy$为凸

仿射映射： f : R n → R , A ∈ R n ∗ m , b ∈ R n , g ( x ) = f ( A x + b )      d o m    g = { x ∣ A x + b ∈ d o m f } f:\R^n\rightarrow\R,A\in\R^{n*m},b\in\R^n,g(x)=f(Ax+b)\;\;dom \;g=\{x|Ax+b\in dom f\} f:Rn→R,A∈Rn∗m,b∈Rn,g(x)=f(Ax+b)domg={ x∣Ax+b∈domf}

证明：令$x,y\in domg,0\le \theta \le 1$
$$\begin{gathered} g(\theta x+(1-\theta )y)=f(\theta Ax+(1-\theta )Ay+b) \\ =f(\theta (Ax+b)+(1-\theta )(Ay+b)) \\ \le \theta f(Ax+b)+(1-\theta )f(Ay+b) \\ =\theta g(x)+(1-\theta )g(y) \end{gathered}$$

$f_i:{\mathbb{R}}^n\to \mathbb{R},i=1,\cdots ,m$为凸，$A\in {\mathbb{R}}^n,b\in \mathbb{R},g(x)=A^T[f_1(x)\cdots f_m(x){]}^T+b$

$A$如果非负，是凸函数

二、两个函数的极大值函数

$f_1,f_2$是凸函数，定义： f ( x ) = max ⁡ { f 1 ( x ) , f 2 ( x ) } , d o m f = d o m f 1 ∩ d o m f 2 f(x)=\max\{f_1(x),f_2(x)\},dom f=dom f_1\cap dom f_2 f(x)=max{ f1​(x),f2​(x)},domf=domf1​∩domf2​

$x,y\in domf,0\le \theta \le 1$
f ( θ x + ( 1 − θ ) y ) = max ⁡ { f 1 ( θ x + ( 1 − θ ) y ) , f 2 ( θ x + ( 1 − θ ) y ) } ≤ max ⁡ { θ f 1 ( x ) + ( 1 − θ ) f 1 ( y ) , θ f 2 ( x ) + ( 1 − θ ) f ( y ) } ≤ max ⁡ { θ f 1 ( x ) , θ f 2 ( x ) } + max ⁡ { ( 1 − θ ) f 1 ( y ) , ( 1 − θ ) f 2 ( y ) } = θ f ( x ) + ( 1 − θ ) f ( y ) f(\theta x+(1-\theta)y)=\max\{f_1(\theta x+(1-\theta)y),f_2(\theta x+(1-\theta)y)\}\\\le\max\{\theta f_1(x)+(1-\theta) f_1(y),\theta f_2(x)+(1-\theta)f(y)\}\\\le\max\{\theta f_1(x),\theta f_2(x)\}+\max\{(1-\theta)f_1(y),(1-\theta)f_2(y)\}\\=\theta f(x)+(1-\theta)f(y) f(θx+(1−θ)y)=max{ f1​(θx+(1−θ)y),f2​(θx+(1−θ)y)}≤max{ θf1​(x)+(1−θ)f1​(y),θf2​(x)+(1−θ)f(y)}≤max{ θf1​(x),θf2​(x)}+max{ (1−θ)f1​(y),(1−θ)f2​(y)}=θf(x)+(1−θ)f(y)

max ⁡ { a + b , c + d } ≤ max ⁡ { a , c } + max ⁡ { b , d } \max\{a+b,c+d\}\le\max\{a,c\}+\max\{b,d\} max{ a+b,c+d}≤max{ a,c}+max{ b,d}

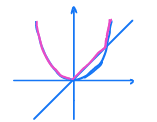
例： f ( x ) = max ⁡ { x 2 , x } f(x)=\max\{x^2,x\} f(x)=max{ x2,x}

例：向量中$r$个最大元素的和

$x\in {\mathbb{R}}^{n}x[i]\to 第i大的元素$
$x[1]\ge x[2]\ge \cdots \ge x[r]\ge \cdots \ge x[n]$
f ( x ) = ∑ i = 1 r x [ i ] f ( x ) = max ⁡ { x i 1 + ⋯ + x i r ∣ 1 ≤ i 1 ≤ ⋯ ≤ i r ≤ n } f(x)=\sum_{i=1}^rx[i]\\f(x)=\max\{x_{i1}+\cdots+x_{ir}|1\le i_1\le\cdots\le i_r\le n\} f(x)=i=1∑r​x[i]f(x)=max{ xi1​+⋯+xir​∣1≤i1​≤⋯≤ir​≤n}

三、无限个凸函数的极大值

$f(x,y)$对于$x$为凸，$\forall y\in A$
$$g=\underset{y\in A}{\sup }f(x,y)$$

例：实对称矩阵的最大特征值

$$\begin{gathered} f(x)={\lambda }_{max}(x),domf=S^m \\ Xy=\lambda y\iff y^{T}Xy=y^T\lambda y \\ \iff y^{T}Xy=\lambda ||y|{|}_2^2 \\ \iff \lambda =\frac{y^{T}Xy}{||y|{|}_2^2} \end{gathered}$$

其中$$\lambda =y^{X}y,||y|{|}_2=1$$

所以 λ m a x ( x ) = sup ⁡ { y T X y ⏟ 对 X 是 凸 函 数 ∣    ∣ ∣ y ∣ ∣ 2 = 1 } \lambda_{max}(x)=\sup\{\underset{对X是凸函数}{\underbrace{y^TXy}}\Big|\;||y||_2=1\} λmax​(x)=sup{ 对X是凸函数 yTXy​​∣∣∣​∣∣y∣∣2​=1}

下一章传送门：中科大-凸优化 笔记（lec15）-保持函数凸性的操作