全部笔记的汇总贴(视频也有传送门):中科大-凸优化
一、凸函数的扩展
f : R n → R f:\R^n\rightarrow\R f:Rn→R为凸函数, d o m f = C ⊆ R n dom\;f=C\subseteq\R^n domf=C⊆Rn
f ~ = { f ( x ) x ∈ d o m f + ∞ x ∉ d o m f \tilde{f}=\left\{ \begin{array}{l} f(x)\;\;\;x\in dom\;f \\ \\+\infty\;\;\;\;x\notin dom\;f \end{array} \right. f~=⎩⎨⎧f(x)x∈domf+∞x∈/domf f ~ : R n → R d o m f ~ = R n \tilde{f}:\R^n\rightarrow\R\\ dom \tilde{f}=\R^n f~:Rn→Rdomf~=Rn
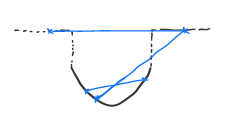
示性函数是凸函数
凸集 C ⊆ R n , f C ( x ) = { 无 定 义 x ∉ C 0 x ∈ C C \subseteq\R^n,f_C(x)=\left\{ \begin{array}{l} 无定义\;\;x\notin C\\ \\0\;\;\;\;x\in C \end{array} \right. C⊆Rn,fC(x)=⎩⎨⎧无定义x∈/C0x∈C
I C ( x ) = { ∞ x ∉ C 0 x ∈ C J C ( x ) = { 1 x ∉ C 0 x ∈ C I_C(x)=\left\{ \begin{array}{l} \infty\;\;x\notin C\\ \\0\;\;\;\;x\in C \end{array} \right.\;\;\;\;\;\;\;\;J_C(x)=\left\{ \begin{array}{l} 1\;\;\;\;x\notin C\\ \\0\;\;\;\;x\in C \end{array} \right. IC(x)=⎩⎨⎧∞x∈/C0x∈CJC(x)=⎩⎨⎧1x∈/C0x∈C
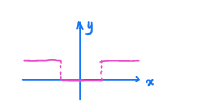
二、一阶条件
设 f : R n → R f:\R^n\rightarrow\R f:Rn→R可微,即梯度 ∇ f \nabla f ∇f在 d o m f dom f domf上均存在,则 f f f为凸,等价于:
- d o m f dom f domf为凸集
- f ( y ) ≥ f ( x ) + ∇ f T ( x ) ( y − x ) , ∀ x , y ∈ d o m f f(y)\ge f(x)+\nabla f^T(x)(y-x),\;\;\forall x,y\in dom f f(y)≥f(x)+∇fT(x)(y−x),∀x,y∈domf
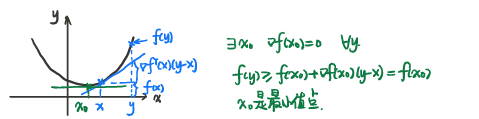
证明一阶条件:
考虑一维情况: f : R → R f:\R\rightarrow\R f:R→R为凸 ⇔ d o m f \Leftrightarrow dom f ⇔domf为凸,且 f ( y ) ≥ f ( x ) + f ′ ( x ) ( y − x ) f(y)\ge f(x)+f'(x)(y-x) f(y)≥f(x)+f′(x)(y−x)
- 先证明( ⇒ \Rightarrow ⇒)
f f f为凸函数, x , y ∈ d o m f x,y\in dom f x,y∈domf为凸集
∀ t 0 < t ≤ 1 x + t ( y − x ) ∈ d o m f \forall t\;\;0<t\le1\;\;x+t(y-x)\in dom f ∀t0<t≤1x+t(y−x)∈domf
f ( x + t ( y − x ) ) ≤ ( 1 − t ) f ( x ) + t f ( y ) f(x+t(y-x))\le(1-t)f(x)+tf(y) f(x+t(y−x))≤(1−t)f(x)+tf(y)
t f ( y ) ≥ t f ( x ) + f ( x + t ( y − x ) ) − f ( x ) tf(y)\ge tf(x)+f(x+t(y-x))-f(x) tf(y)≥tf(x)+f(x+t(y−x))−f(x)
f ( y ) ≥ f ( x ) + f ( x + t ( y − x ) ) − f ( x ) t f(y)\ge f(x)+\frac{f(x+t(y-x))-f(x)}t f(y)≥f(x)+tf(x+t(y−x))−f(x)
对 f ( x + t ( y − x ) ) − f ( x ) f(x+t(y-x))-f(x) f(x+t(y−x))−f(x)使用泰勒展开式,两边取极限 lim t → 0 + ⇒ f ( y ) ≥ f ( x ) + f ′ ( y ) ( y − x ) \lim_{t\rightarrow0_+}\Rightarrow f(y)\ge f(x)+f'(y)(y-x) t→0+lim⇒f(y)≥f(x)+f′(y)(y−x)
- 再证明( ⇐ \Leftarrow ⇐)
设 ∀ x ≠ y , x , y ∈ d o m f \forall x\neq y,x,y\in dom f ∀x=y,x,y∈domf
0 ≤ θ ≤ 1 0\le\theta\le1\;\;\;\; 0≤θ≤1构造 z = θ x + ( 1 − θ ) y ∈ d o m f z=\theta x+(1-\theta)y\in dom f z=θx+(1−θ)y∈domf
f ( x ) ≥ f ( z ) + f ′ ( z ) ( x − z ) f(x)\ge f(z)+f'(z)(x-z) f(x)≥f(z)+f′(z)(x−z)
f ( y ) ≥ f ( z ) + f ′ ( z ) ( y − z ) f(y)\ge f(z)+f'(z)(y-z) f(y)≥f(z)+f′(z)(y−z)
θ f ( x ) + ( 1 − θ ) f ( y ) ≥ f ( z ) ⏟ 凸 函 数 + f ′ ( z ) ( θ ( x − z ) + ( 1 − θ ) ( y − z ) ) ⏟ θ x + ( 1 − θ ) y − z = 0 \underset{凸函数}{\underbrace{\theta f(x)+(1-\theta)f(y)\ge f(z)}}+f'(z)\underset{\theta x+(1-\theta)y-z=0}{\underbrace{\Big(\theta(x-z)+(1-\theta)(y-z)\Big)}} 凸函数 θf(x)+(1−θ)f(y)≥f(z)+f′(z)θx+(1−θ)y−z=0 (θ(x−z)+(1−θ)(y−z))
下一章传送门:中科大-凸优化 笔记(lec11)-凸函数:二阶条件