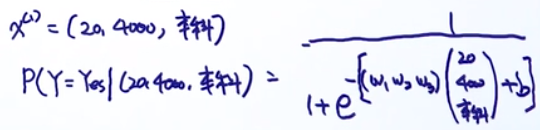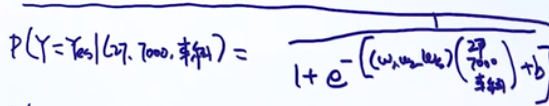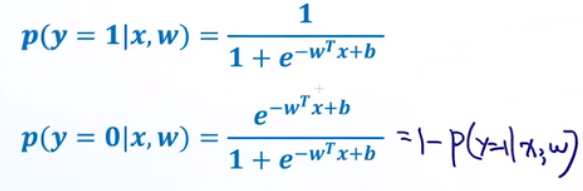12[NLP训练营]逻辑斯蒂回归

公式输入请参考： 在线Latex公式

常用场景

·贷款违约情况（会违约/不会违约）
·广告点击问题（会点击/不会点击）
·商品推荐（会购买/不会购买）
·情感分析（正面/负面）
·疾病诊断（阳性/阴性）
·还有其他很多分类问题……此外这个算法可以用来做baseline，很好。
分类实例：

年龄，总之，学历可以看做输入X，是否逾期可以看做标签Y
目的是学习 $f:X\to Y$映射关系，这种关系我们也可以定义为一种条件概率：
$P(Y|X)$
现在两个问题：
1、这个条件概率 $P(Y|X)$怎么算？
实际上就是求 $P(Y|年龄，工资，学历)$，例如： $P(1|20，4000，本科)$
2、假设我们明确知道条件概率 $P(Y|X)$，怎么做分类？
分别求 $P(Y=1|X)$和$P(Y=0|X)，然后比较大小即可

问题1

条件概率 $P(Y|X)$怎么表示？
这相当于用模型来捕获输入X和输出y之间的关系
这个关系可以是线性，也可以是非线性的。现在在讲逻辑回归，所以我们考虑
可不可以用线性回归来表示 $P(Y|X)=w^Tx+b$？为什么？
答案是否，原因是等式左边是一个条件概率，因此它有两个限制：
1、值域是[0,1]
2、所有y的概率加起来等于1： $\sum_yp(y|x)=1$，这里用二分类来看就很容易理解，丢硬币就是正面和反面，两个面出现的概率和是1。
等式的右边明显是不可能满足第一个条件的（ $-\infty<w^Tx+b<+\infty$），所以这个等式不能成立。
现在就是要把 $w^Tx+b$的值域弄到[0,1]
到时候就该祭出sigmoid函数了：

Logistic Function

sigmoid就是逻辑函数的一种。

把sigmoid函数写为： $y=\sigma(x)$，把上面等式的左边写到sigmoid函数里面就可以得到概率函数的形式了：
$p(y|x,w)=\sigma(x)=\sigma(w^Tx+b)$
展开：
$p(y|x,w)=\cfrac{1}{1+e^{-(w^Tx+b)}}$
这里面w是一个向量，T代表转置，b是bias，是一个实数。
再回到原来的例子，我们看第一个样本可以写为：
$x^{(1)}=(20，4000，本科)$
我们可以把这个东西理解为特征向量。
这里的参数w，由于有3个特征，所以参数也是3维的。b是一个实数。
有了这些，我们就可以写出第一个样本的条件概率的式子：

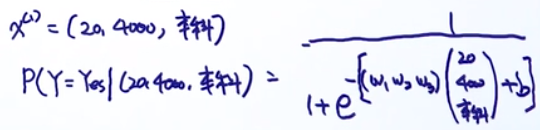
通过已有的样本，我们可以计算出参数w，b。
那么，最后一个需要预测最后一个样本被拒的概率写为：

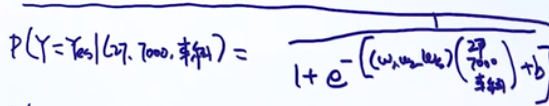
同样可以写出Y=No的概率，由于是二分类问题：P(Y=No)=1-P(Y=Yes)

问题2

对于二分类问题(懒得打公式，下面e的指数少了括号)：

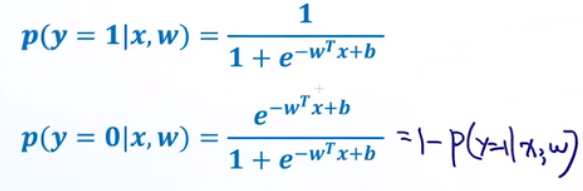
两个式子可以合并成：
$p(y|x,w)=p(y=1|x,w)^y[1-p(y=1|x,w)]^{1-y}$

决策边界

决策边界，AKA decision boundary。是用来判断一个模型是不是线性分类器。

根据这个我们知道逻辑斯蒂回归是线性分类器，现在来看这个边界咋求出来是一根线。
由于我们分类器是一个条件概率，那么在边界线上的点分为正样本和负样本的概率相等：
$p(y=1|x,w)=p(y=0|x,w)$
把上面的公式代入，并把分母消去：
$1=e^{-(w^Tx+b)}$
两边同时取log
$-(w^Tx+b)=log1\to w^Tx+b=0$
这个就是一个直线，说明边界是一个直线。

Objective Function

假设我们拥有数据集 $D=\{(x_i,y_i)\}_{i=1}^n \space x\in R^d,y_i\in\{0,1\}$，n是样本数
而且我们已经定义了：
$p(y|x,w)=p(y=1|x,w)^y[1-p(y=1|x,w)]^{1-y}$
我们需要最大化目标函数：
$\widehat w_{MLE},\widehat b_{MLE}=arg\underset{w,b}{max}\prod_{i=1}^np(y_i|x_i,w,b)$
下面是推导，先取log，连乘变连加，另外可以避免小于1的数字连乘造成的underflow：
$\widehat w_{MLE},\widehat b_{MLE}=arg\underset{w,b}{max}log\sum_{i=1}^np(y_i|x_i,w,b)\\ =arg\underset{w,b}{max}\sum_{i=1}^nlogp(y_i|x_i,w,b)$
取负号，使得求最大值变成求最小值：
$\widehat w_{MLE},\widehat b_{MLE}=arg\underset{w,b}{min}-\sum_{i=1}^nlogp(y_i|x_i,w,b)$
把逻辑回归的条件概率定义带入：
$\widehat w_{MLE},\widehat b_{MLE}=arg\underset{w,b}{min}-\sum_{i=1}^nlog[p(y_i=1|x_i,w)^{y_i}[1-p(y_i=1|x_i,w)]^{1-y_i}]$

---

根据这个把上式化简
$log(a^xb^y)=log(a^x)+log(b^y)=xloga+ylogb$

---

$\widehat w_{MLE},\widehat b_{MLE}=arg\underset{w,b}{min}-\sum_{i=1}^ny_ilogp(y_i=1|x_i,w)^{y_i}+(1-y_i)log[1-p(y_i=1|x_i,w)]$

Gradient Descent for Logistic Regression

把sigmoid函数带入上面：
$\widehat w_{MLE},\widehat b_{MLE}=arg\underset{w,b}{min}-\sum_{i=1}^ny_ilog\sigma(w^Tx_i+b)+(1-y_i)log[1-\sigma(w^Tx_i+b)]$
把这个看成是w和b的函数(实际上就是损失函数？)，然后求梯度，就是要分别对w和b求偏导数：
$L(w,b)=-\sum_{i=1}^ny_ilog\sigma(w^Tx_i+b)+(1-y_i)log[1-\sigma(w^Tx_i+b)]$

---

$log'x=\cfrac{1}{x}$
$\sigma'(x)=\sigma(x)(1-\sigma(x))$

---

$\cfrac{\partial L(w,b)}{\partial w}=-\sum_{i=1}^ny_i\cfrac{1}{\sigma(w^Tx_i+b)}\sigma(w^Tx_i+b)[1-\sigma(w^Tx_i+b)]x_i+(1-y_i)\cfrac{1}{1-\sigma(w^Tx_i+b)}[-\sigma(w^Tx_i+b)][1-\sigma(w^Tx_i+b)]x_i\\ =-\sum_{i=1}^ny_i[1-\sigma(w^Tx_i+b)]x_i+(y_i-1)\sigma(w^Tx_i+b)x_i\\ =-\sum_{i=1}^n[y_i-\sigma(w^Tx_i+b)]x_i\\ =\sum_{i=1}^n[\sigma(w^Tx_i+b)-y_i]x_i$
从上面看，就是预测值减去真实值。如果预测值等于真实值，那么这项等于0，如果预测与真实值不一样，才会产生cost。
$.$
$\frac{\partial L(w,b)}{\partial b}=-\sum_{i=1}^ny_i\cfrac{1}{\sigma(w^Tx_i+b)}\sigma(w^Tx_i+b)[1-\sigma(w^Tx_i+b)]+(1-y_i)\cfrac{1}{1-\sigma(w^Tx_i+b)}[-\sigma(w^Tx_i+b)][1-\sigma(w^Tx_i+b)]\\ =-\sum_{i=1}^ny_i[1-\sigma(w^Tx_i+b)]+(y_i-1)\sigma(w^Tx_i+b)\\ =-\sum_{i=1}^n[y_i-\sigma(w^Tx_i+b)]\\ =\sum_{i=1}^n[\sigma(w^Tx_i+b)-y_i]$
下面开始梯度下降的算法
1、初始化 $w^1,b^1$
2、开始迭代循环：
$w^{t+1}=w^t-\eta \sum_{i=1}^n[\sigma(w^Tx_i+b)-y_i]x_i$
$b^{t+1}=b^t-\eta \sum_{i=1}^n[\sigma(w^Tx_i+b)-y_i]$

Stochastic Gradient Descent for Logistic Regression

可以看到，上面的梯度下降法中有一个求和项，也就是每次梯度更新都要计算所有了样本。因此普通梯度下降不适合大数据样本的计算。
因此对这个算法进行改进：每次只拿一个样本进行梯度更新。这样每次一个样本会被一些极端样本影响，然后每批样本更新n次。
这两种情况都比较极端，可以采取一种折中的方式。每次取一个mini-batch的样本进行更新梯度。mini-batch Gradient Descent